Что такое ферма – Значение слова ФЕРМА. Что такое ФЕРМА?

Ферма (конструкция) — это… Что такое Ферма (конструкция)?

Фе́рма (фр. ferme, от лат. firmus прочный), в строительной механике стержневая система, остающаяся геометрически неизменяемой после замены её жёстких узлов шарнирными. В элементах фермы, при отсутствии расцентровки стержней и внеузловой нагрузки, возникают только усилия растяжения-сжатия. Фермы образуются из прямолинейных стержней, соединенных в узлах.^[1]

ферма 1

Ферма состоит из элементов: пояс, стойка, раскос, шпренгель (опорный раскос).

ферма 2 ферма ж/д моста, используемая в конструкции антенны.

История

Классификация

Фермы классифицируют по следующим признакам:

• Характер очертания внешнего контура
  • Параллельные пояса
  • Ломаные пояса
  • Полигональные пояса
  • Треугольные пояса
• Тип решётки
  • Треугольная
  • Раскосная
  • Полураскосная
  • Ромбическая
• Тип опирания
  • Балочный
  • Арочный
  • Консольный
  • Балочно-консольный
• Назначение
  1. ферма Пратта (с жатыми стойками и растянутыми раскосами)
  2. ферма Уорренна (с решёткой из треугольников)
  3. Бельгийская (треугольная) ферма
  4. ферма с перекрёстными подкосами
  5. ферма под верхний свет
  • Подстропильные
  • Мостовые
  • Крановые
  • Башенные
• Материал исполнения
  • Деревянные
  • Металлические (стальные и алюминиевые)
  • Железобетонные
  • Из полимерных материалов

Область применения

Фермы широко используются в современном строительстве, в основном для перекрытия больших пролётов: мосты, стропильные системы промышленных зданий, спортивные сооружения.Так же данная конструкция может использоваться специалистами при производстве различных видов павильонов, сценических конструкций, тентов и подиумов.

Принцип действия

Если произвольным образом скрепить на шарнирах несколько стержней, то они будут беспорядочно крутиться вокруг друг друга, и подобная конструкция будет, как говорят в строительной механике, «изменяемой», то есть если на неё надавить, то она сложится, как складываются стенки спичечного коробка. Совсем другое дело, если Вы составите из стерженьков обычный треугольник. Теперь, сколько бы Вы ни давили, конструкция сможет сложиться, только если сломать один из стержней, или оторвать его от других. Это конструкция уже «неизменяемая». Конструкция фермы содержит в себе эти треугольники. И стрела башенного крана и сложные опоры, все они состоят из маленьких и больших треугольников.

Важно знать, что так как любые стержни лучше работают на сжатие-растяжение, чем на излом, то нагрузку к ферме следует прикладывать в точках соединения стержней.

Фактически стержни фермы обычно соединяют между собой не через шарниры, а жёстко. То есть, если взять два любых стержня и отрезать их от остальной конструкции, то они не будут вращаться относительно друг друга. Однако, в простейших расчётах этим пренебрегают и считают, что шарнир имеется.

Принцип расчёта ферм вырезанием узлов

Существует огромное количество способов расчёта ферм, как простых, так и сложных. Один из самых простых — расчёт вырезанием узлов. Данный способ подходит для простейших плоских ферм и применяется для обучения студентов ВТУЗов.

Для расчёта фермы все силы, действующие на ферму, сводят к её узлам. После того, как определены силы, действующие на ферму, считают реакции опор фермы. После того, как реакции определены, берут любой узел, в котором встречаются только 2 стержня и приложены какие-либо силы. Мысленно обрезают остальную часть фермы и получают узел, в котором встречаются несколько известных сил (например, реакции опор) и две неизвестных силы — те усилия, которые действуют в необрезанных нами стержнях фермы. Находят неизвестные усилия в стержнях, составляя уравнения равенства сил по любым двум осям. Далее, зная эти усилия, вырезают следующий узел и т. д., пока не будут найдены усилия во всех стержнях.

Примеры

См. также

Примечания

1. ↑ Дарков А.В. Строительная механика. — М.: Высшая школа, 1986. — 607 с.: ил.

Ссылки

dic.academic.ru

Что такое ферма в строительстве?

Фермы. Область применения. Классификация. Конструкции ферм.

Фермой называют решетчатую конструкцию из стержней, соединенных между собой в узлах и образующих геометрически неизменяемую конструкцию.

Если нагрузка приложена в узлах, а оси элементов фермы пересекаются в одной точке (центре узла), то жесткость узлов несущественно влияет на работу конструкции и в большинстве случаев их можно рассматривать как шарнирные. Тогда все стержни фермы испытывают только осевые усилия (растяжение или сжатие). Благодаря этому металл в фермах используется более рационально, чем в балках, и они экономичнее балок по расходу материала, но более трудоемки в изготовлении, поскольку имеют большое число деталей. С увеличением перекрываемых пролетов и уменьшением нагрузки эффективность ферм по сравнению со сплошностенчатыми балками растет.

По материалу различают фермы стальные, деревянные, ж/бетонные

Стальные фермы получили широкое распространение во многих областях строительства: в покрытиях и перекрытиях промышленных и гражданских зданий, мостах, опорах линий электропередачи, объектах связи, телевидения и радиовещания (башни, мачты), транспортерных галереях, гидротехнических затворах, грузоподъемных кранах и т.д.

Фермы бывают плоскими и пространственными.

Плоские фермы могут воспринимать нагрузку, приложенную только в их плоскости, и нуждаются в закреплении из своей плоскости связями или другими элементами. Пространственные фермы образуют жесткий пространственный брус, способный воспринимать нагрузку, действующую в любом направлении. Каждая грань такого бруса представляет собой плоскую ферму. Примером пространственного бруса может служить башня или мачта

Основными элементами ферм являются пояса, образующие контур фермы, и решетка, состоящая из раскосов и стоек.

Расстояние между узлами пояса называют панелью (d), расстояние между опорами — пролетом (L), расстояние между осями (или наружными гранями) поясов — высотой фермы (h_ф).

 

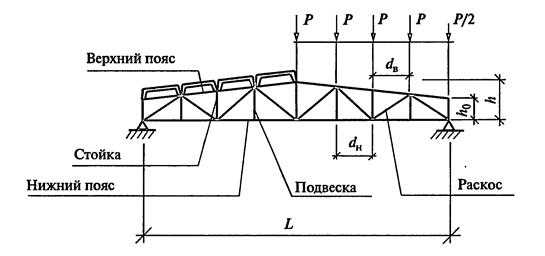
Соединения элементов в узлах осуществляют путем непосредственного примыкания одних элементов к другим или с помощью узловых фасонок. Для того чтобы стержни ферм работали в основном на осевые усилия, а влиянием моментов можно было пренебречь, элементы ферм следует центрировать по осям.

В зависимости от назначения, архитектурных требований и схемы приложения нагрузок фермы могут иметь самую разнообразную конструктивную форму. Их можно классифицировать по следующим признакам: статической схеме, очертанию поясов, системе решетки, способу соединения элементов в узлах, величине усилия в элементах.

По статической схеме фермы бывают: балочные (разрезные, неразрезные, консольные), арочные, рамные и вантовые.

В покрытиях зданий, мостах, транспортерных галереях и других подобных сооружениях наибольшее применение нашли балочные разрезные системы. Они просты в изготовлении и монтаже, не требуют устройства сложных опорных узлов.

При числе перекрываемых пролетов два и более применяют неразрезные фермы. Они экономичнее по расходу металла и обладают большей жесткостью, что позволяет уменьшить их высоту. Но как во всяких внешне статически неопределимых системах, в неразрезных фермах усложняется монтаж таких конструкций. Консольные фермы используют для навесов, башен, опор воздушных линий электропередач. Рамные системы экономичны по расходу стали, имеют меньшие габариты, однако более сложны при монтаже. Их применение рационально для большепролетных зданий. Применение арочных систем, хотя и дает экономию стали, приводит к увеличению объема помещения и поверхности ограждающих конструкций. Их применение диктуется в основном архитектурными требованиями. В вантовых фермах все стержни работают только на растяжение и могут быть выполнены из гибких элементов, например стальных тросов. Растяжение всех элементов таких ферм достигается выбором очертания поясов и решетки, а также созданием предварительного напряжения. Работа только на растяжение позволяет полностью использовать высокие прочностные свойства стали, поскольку снимаются вопросы устойчивости. Вантовые фермы рациональны для большепролетных перекрытий и в мостах.

 

В зависимости от очертания поясов фермы подразделяют на треугольные (а,б), арочные (д), полигональные (е), трапецеидальные (в), с параллельными поясами (г).

Очертание поясов ферм в значительной степени определяет их экономичность. Теоретически наиболее экономичной по расходу стали является ферма, очерченная по эпюре моментов. Для однопролетной балочной системы с равномерно распределенной нагрузкой это будет сегментная (арочная) ферма с параболическим поясом (д). Однако криволинейное очертание пояса повышает трудоемкость изготовления, поэтому такие фермы в настоящее время практически не применяют.

Более приемлемым является полигональное очертание с переломом пояса в каждом узле (е).

Стропильная ферма — выбор схемы

Оно достаточно близко соответствует параболическому очертанию эпюры моментов, не требует изготовления криволинейных элементов. Такие фермы иногда применяют для перекрытия больших пролетов и в мостах, т.е. в конструкциях, поставляемых на строительную площадку «россыпью» (из отдельных элементов). Для ферм покрытий обычных зданий, поставляемых на монтаж, как правило, в виде укрупненных отправочных элементов из-за усложнения изготовления эти фермы в настоящее время не применяют. Вы их можете встретить только в старых сооружениях, построенных до 50-х годов.

Фермы трапецеидального очертания (в) , хотя и не совсем соответствуют эпюре моментов, имеют конструктивные преимущества, прежде всего за счет упрощения узлов. Кроме того, применение таких ферм в покрытии позволяет устроить жесткий рамный узел, что повышает жесткость каркаса.

Фермы с параллельными поясами по своему очертанию далеки от эпюры моментов и по расходу стали не экономичны.

Однако равные длины элементов решетки, одинаковая схема узлов, наибольшая повторяемость элементов и деталей и возможность их унификации способствует индустриализации их изготовления. Благодаря этим преимуществам фермы с параллельными поясами стали основными для покрытия зданий.

Фермы треугольного очертания рациональны для консольных систем, а также для балочных систем при сосредоточенной нагрузке в середине пролета (подстропильные фермы).

Системы решетки

Выбор типа решетки зависит от схемы приложения нагрузок, очертания поясов и конструктивных требований. Так, во избежание изгиба пояса места приложения сосредоточенных нагрузок следует подкреплять элементами решетки. Для обеспечения компактности узлов угол между раскосами и поясом желательно иметь в пределах 30…50°.

Для снижения трудоемкости изготовления ферма должна быть по возможности простой с наименьшим числом элементов и дополнительных деталей.

Треугольная система решетки имеет наименьшую суммарную длину элементов и наименьшее число узлов. Различают фермы с восходящими и нисходящими опорными раскосами. Если опорный раскос идет от нижнего опорного узла фермы к верхнему поясу, то его называют восходящим. При направлении раскоса от опорного узла верхнего пояса к нижнему — нисходящим. В местах приложения сосредоточенных нагрузок (например, в местах опирания прогонов кровли) можно установить дополнительные стойки или подвески. Эти стойки служат также для уменьшения расчетной длины пояса. Стойки и подвески работают только на местную нагрузку.

Недостатком треугольной решетки является наличие длинных сжатых раскосов, что требует дополнительного расхода стали для обеспечения их устойчивости.

 

 

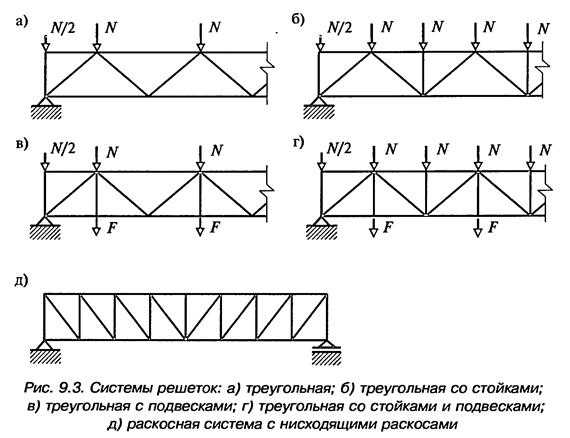
В раскосной системе решетки все раскосы имеют усилия одного знака, а стойки — другого. Так, в фермах с параллельными поясами при восходящем раскосе стойки растянуты, а раскосы сжаты; при нисходящем — наоборот. Очевидно, при проектировании ферм следует стремиться, чтобы наиболее длинные элементы были растянуты, а сжатие воспринималось короткими элементами. Раскосная решетка более металлоемка и трудоемка по сравнению с треугольной, так как общая длина элементов решетки больше и в ней больше узлов. Применение раскосной решетки целесообразно при малой высоте ферм и больших узловых нагрузках.

Шпренгельную решетку применяют при внеузловом приложении сосредоточенных нагрузок к верхнему поясу, а также при необходимости уменьшения расчетной длины пояса. Она более трудоемка, но в результате исключения работы пояса на изгиб и уменьшения его расчетной длины может обеспечить снижение расхода стали.

Если нагрузка на ферму может действовать как в одном, так и в другом направлении (например, ветровая нагрузка), то целесообразно применение крестовой решетки.

 

Ромбическая и полураскосная решетки благодаря двум системам раскосов обладают большой жесткостью; эти системы применяют в мостах, башнях, мачтах, связях для уменьшения расчетной длины стержней. Они рациональны при большой высоте ферм и работе конструкций на значительные поперечные силы.

Возможна в одной ферме комбинация различных типов решетки.

По способу соединения элементов в узлах фермы подразделяют на сварные и болтовые. В конструкциях, изготовленных до 50-х годов, применялись также клепаные соединения. Основными типами ферм являются сварные. Болтовые соединения, как правило, на высокопрочных болтах применяют в монтажных узлах.

Железобетонные фермы и некоторые тяжелые стальные фермы могут выполняться без раскосов с жесткими узлами.

Высоту ферм принимают h= (1/5 – 1/4)L, высоту ферм с параллельными поясами и трапецеидальных ферм — h= (1/6 – 1/8)L. Наклон раскосов составляет 35⁰ – 45⁰.

 

Стальные фермы.

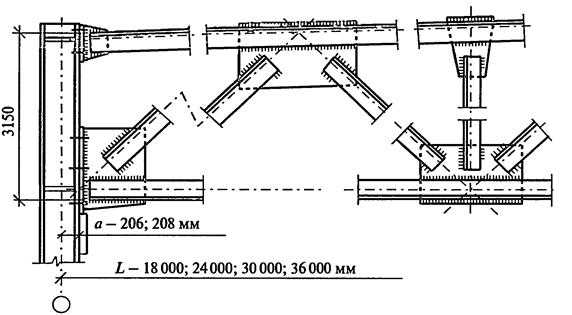
В зависимости от пролета и величины действующей нагрузки условно различают легкие фермы с сечениями элементов из простых прокатных или гнутых профилей (при усилиях в стержнях N<500кН и пролетом до 50 метров) и тяжелые фермы с элементами составного сечения (N >500кН), способные перекрывать пролеты до 100 метров. Легкие стальные фермы разработаны для пролетов 18, 24, 30, 36 метров с унифицированным размером панелей 3 м, высотой 2,25м, 2,4м, 3,15 метра (с учетом габаритов грузов, перевозимых ж/д транспортом).

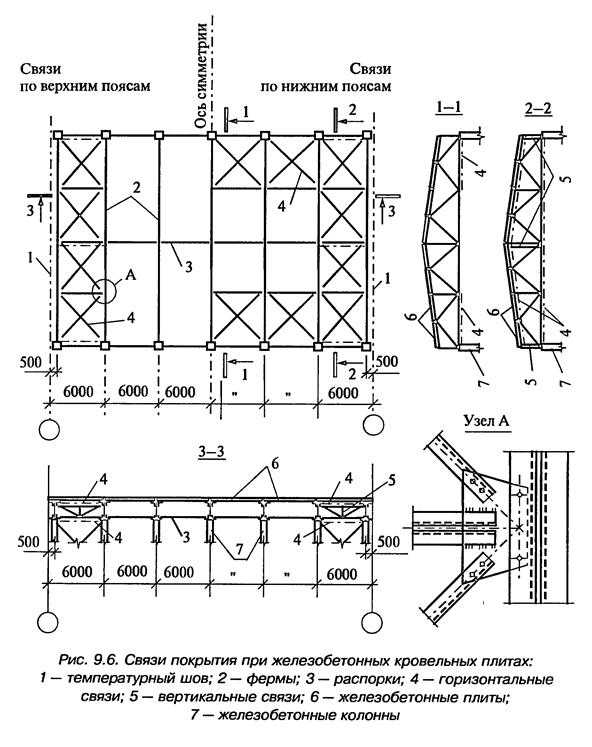
Пространственную жесткость обеспечивают постановкой горизонтальных и вертикальных связей. Также в обеспечении жесткости участвуют прогоны и плиты перекрытия.

 

 

Предыдущая21222324252627282930313233343536Следующая

---

Дата добавления: 2016-05-11; просмотров: 3432;

---

ПОСМОТРЕТЬ ЕЩЕ:

stroyvolga.ru

это что такое? Строительная конструкция

Самое распространенное значение слова «ферма» – сельскохозяйственное предприятие, предназначенное для животноводства. Но сейчас речь не о месте ведения подсобного хозяйства. Здесь собрана вся информация о вероятно древнейшей строительной конструкции, которая до сих пор актуальна в современной жизни. Она имеет широкое применение в строительстве, особенно в конструировании мостов и спортивных сооружений.

Ферма – это система, состоящая из стержней, которая остается геометрически неизменной при смене ее жестких узлов шарнирными. К ней также относятся и шпренгельные балки, которые представлены комбинацией из двух- или трехпролетной неразрезанной балки и подпружной тяги.

Где используется?

Как уже упоминалось, ферма в строительстве является незаменимым элементом. С ее помощью строители облегчают конструкцию сооружения и уменьшают расход необходимых материалов. Без использования фермы не обходится строительство мостов, стадионов, ангаров, а также декоративных сооружений, таких как павильоны, сцены, подиумы и т.д.

При проектировке корпуса корабля, самолета, тепловоза расчет прочности происходит таким же способом, как и расчет нагрузки на ферму.

Классификация

Ферма – это конструкция, состоящая из стержней, которые связаны между собой в узлах и образуют статически неизменную систему. Классификация ферм может быть проведена по множеству свойств.

По грузоподъемности конструкции

• Легкие. В них используется одностенчатое сечение. Легкие фермы чаще всего используются в промышленном строительстве.
• Тяжелые. Тяжелые фермы применяются в конструкции башенных кранов, спортивных стадионов и т.д. В них используются стержни более сложного сечения, нежели в легких. Как правило, они состоят из двух-трех частей из-за большой расчетной длины и возлагаемой на них нагрузки. Чаще всего используют двухстенчатое сечение с двухплоскостным узловым сопряжением.

По общим признакам

• По назначению. По назначению фермы бывают башенные, мостовые, крановые, фермы покрытия, опорные конструкции и т.д.
• По типу материала. Дерево, сталь, алюминий, железобетон и т.д. – из всего этого может быть изготовлена строительная ферма. Это существенное достоинство данной системы. Также можно комбинировать несколько видов материала.
• По особенностям конструкции. Существуют разнообразные типы сечения, типы решетки, виды опорных конструкций, а также типы поясов строительной конструкции фермы.

По пространственному признаку

• Плоские. Фермы берут на себя вертикальную нагрузку, т.к. х стержни располагаются в одной плоскости.
• Пространственные. Распределяют нагрузку по всей своей площади. Пространственная ферма образована из множества плоских ферм, объединённых между собой особыми способами.

По типу

• Балка Виренделя.
• Ферма Уоррена.
• Ферма Пратта.
• Ферма Больмана.
• Ферма Финка.
• Треугольная ферма.
• Кингпост.
• Ферма с перекрестными подкосами.
• Решетчатая городская конструкция.
• Ферма под верхний свет.

Особенности конструкции

Классификация фермы по особенности конструкции достаточно обширна. Далее каждая из особенностей будет рассмотрена более детально.

Типы сечения

Поперечное сечение в строительной ферме выполнено из прокатных профилей. Оно может быть в виде:

• Уголка (одиночного или двойного).
• Трубы (круглой или квадратной).
• Швелера.
• Тавра или двутавра.

Типы пояса

Очертания пояса могут быть представлены в виде:

• Трапеции. Его достоинство заключается в том, что такой вид пояса ужесточает рамный узел, соответственно, вместе с ним увеличивается и жесткость здания.
• Треугольника. Такой вид пояса используют для балочных и консольных систем. Он имеет массу недостатков, таких как нерациональный расход металла при распределении нагрузки, сложность опорного узла и т.д.
• Параболы. Данный пояс является самым трудоемким. Поэтому сегментные фермы используются очень редко.
• Многоугольника. Полигональные фермы применяются чаще, чем сегментные. Т.к. в них перелом в узлах конструкции не так ощутим.
• Параллельных поясов. Чаще всего используются для покрытия промышленных зданий. Они имеют идентичную схему узлов, равные по размеру элементы решетки, также они обладают повторяемостью элементов и деталей.

Типы решетки

Существуют шесть типовых вариантов решетки:

• Треугольная.
• Ромбическая.
• Шпренгельная.
• Крестовая.
• Раскосая.
• Полураскосая.

Типы опоры

Существуют 5 видов опорных конструкций. Для того чтобы выбрать опорный узел, нужно знать схему расчёта. От нее зависит, будет ли опорный узел шарнирным или жестким. Виды опор:

• Балочная или консольная.
• Арочная.
• Вантовая.
• Рамная.
• Комбинированная.

Принцип действия

Уникальность этой конструкции заключается в ее «неизменности» под воздействием внешних факторов. Нагрузка на эту систему бывает достаточно большая. Ферма представляет собой множество объединённых в одну конструкцию треугольников. Нагрузка в них сосредоточена в месте соединения узлов, т.к. стержни лучше проявляют свои свойства в процессе сжатия-растяжения, а не на излом. В современном строительстве чаще всего используют жесткое, а не шарнирное соединение стержней. Из этого следует, что при отделении одного из них от цельной конструкции они останутся в неизменном по отношению друг к другу положении.

Принцип расчета ферм вырезанием углов

Этот способ расчета ферм является самым простым. Данный способ преподают во многих технических учебных заведениях.

Ферма – это конструкция, нагрузка на которую сосредоточена в ее узлах. Следовательно, нужно рассчитать все внешние факторы, которые будут являться нагрузкой на узлы. Затем — вычислить реакцию опоры и найти узел, в котором присутствуют 2 стержня с приложенной на них силой. Условно необходимо отделить всю остальную часть фермы и получить узел, в котором будет несколько известных значений и 2 неизвестных. Затем нужно составить равенство по двум осям и рассчитать неизвестные значения. Таким же образом выделяют следующий узел, и так до тех пор, пока ферма не будет рассчитана.

Основные типы ферм

• Балка Виренделя – это система, где все ее части образуют прямоугольные отверстия и тем самым соединяются в жесткую раму. Она по своей конструкции не подходит под строгий термин «фермы», т.к. в этой балке отсутствует пара сил. Ее разработал бельгийский инженер Артур Вирендель. Но т.к. эта конструкция достаточно массивна, ее редко можно встретить в современной архитектуре.

• Ферма Уоррена. Это упрощенная версия конструкции Пратта-Хова. Она работает по принципу сжатия-растяжения. Чаще всего выполнена из стального проката.
• Ферма Пратта. Патент на данное сооружение принадлежит отцу и сыну из Бостона. Калеб Пратт и Томас Уилсон были двумя инженерами. Они использовали сжатые части по вертикали, а растянутые — по горизонтали. Поэтому нагрузка одинаково хорошо распределяется как сверху, так и снизу.
• Ферма Больмана имеет достаточно сложную и неудобную конструкцию. Свою популярность в США данное сооружение получило из-за политических достоинств ее создателя. Изобретатель красноречиво говорил про ферму, пусть даже и не все соответствовало действительности. Больман сумел продвинуть свое изобретение с помощью американского правительства, которое порой принуждало градостроителей использовать данную конструкцию при проектировке мостов. Среди обладателей патентов строительных ферм есть немало наших соотечественников, но еще ни одна «русская» ферма не продвигалась в массы столь оригинальным способом.
• Ферма Финка является упрощенной версией фермы Больмана. Он просто укоротил все ее элементы и тем самым сделал ее более эффективной. Также она имеет схожесть с конструкцией фермы Пратта. Она отличается от нее лишь отсутствием нижней балки.
• Треугольная ферма. Также ее называют «бельгийской». Это современная конструкция, которая представлена в виде треугольников со шпренгелями.
• Кингпост — самый простой вариант фермы. Он представляет собой пару опор, опирающихся на вертикальную балку.
• Решётчатая городская структура была создана для замены огромных деревянных мостов. Она достаточно проста по своей конструкции. Для нее применяют обычные деревянные доски, присоединённые друг к другу под углом, которые, в свою очередь, образуют решетку.

fb.ru

ферма — это… Что такое ферма?

ферма́та — фермата …   Русское словесное ударение

ФЕРМА — плоская конструкция, состоящая из соединенных между собой отдельных стержней или дисков, перекрывающая отверстие между опорами и передающая на последние воспринимаемую ею нагрузку. Арочная ферма Изготовляется из металла, дерева или железобетона.… …   Технический железнодорожный словарь

ФЕРМА — (фр. ferme, от лат. firme крепко, прочно). 1) арендуемый деревенский дом, при котором есть сад, скотный двор, а иногда и пахотная земля; то же, что мыза, хутор. 2) в Петербурге молочная ферма есть просто приют для дойных коров, откуда отпускают… …   Словарь иностранных слов русского языка

ФЕРМА — • ФЕРМА (Fermat) Пьер де (1601 65), французский математик. Вместе с Блезом ПАСКАЛЕМ сформулировал теорию вероятности и, доказав, что свет перемещается по самой короткой оптической траектории (принцип Ферма), стал основателем геометрической оптики …   Научно-технический энциклопедический словарь

ФЕРМА — 1. ФЕРМА1, фермы, жен. (франц. ferme) (с. х.). 1. Хозяйственное предприятие, занимающееся какой нибудь специальной отраслью сельского хозяйства. Животноводческая ферма. Молочная ферма. 2. В капиталистических государствах частное… …   Толковый словарь Ушакова

ФЕРМА — 1. ФЕРМА1, фермы, жен. (франц. ferme) (с. х.). 1. Хозяйственное предприятие, занимающееся какой нибудь специальной отраслью сельского хозяйства. Животноводческая ферма. Молочная ферма. 2. В капиталистических государствах частное… …   Толковый словарь Ушакова

Ферма — частное сельскохозяйственное предприятие, принадлежащее фермеру и ведущееся им на собственной или арендованной земле. По английски: Farm Синонимы: Фермерское хозяйство См. также: Сельскохозяйственные предприятия Финансовый словарь Финам …   Финансовый словарь

ферма — ранчо, усадьба, хутор; умет, племхоз, фольварк, хозяйство, консоль Словарь русских синонимов. ферма сущ., кол во синонимов: 24 • виброферма (1) • …   Словарь синонимов

ферма —     ФЕРМА, хозяйство …   Словарь-тезаурус синонимов русской речи

ферма — ферма; колхоз фермани колхозная ферма …   Нанайско-русский словарь

Ферма — – плоская стержневая несущая конструкция. [Терминологический словарь по бетону и железобетону. ФГУП «НИЦ «Строительство» НИИЖБ им. А. А. Гвоздева, Москва, 2007 г. 110 стр.] Ферма – несущая стержневая конструкция, как правило… …   Энциклопедия терминов, определений и пояснений строительных материалов

dic.academic.ru

Ферма что это? Значение слова Ферма

Значение слова Ферма по Ефремовой:

Ферма — 1. Частное крестьянское сельскохозяйственное предприятие на собственной или арендованной земле.
2. Специализированное хозяйственное предприятие совхоза или колхоза, занимающееся определенной отраслью сельского хозяйства. // Хозяйство при сельскохозяйственном учебном заведении.

---

Инженерное сооружение, состоящее из соединенных между собою стержней.

Значение слова Ферма по Ожегову:

Ферма — Частное хозяйство или сельскохозяйственное предприятие на собственном или арендуемом земельном участке

---

Ферма Специализированное звероводческое хозяйство

---

Ферма Животноводческое подразделение в хозяйстве совхоза или колхоза

---

Ферма Сооружение из скрепленных стержней, брусьев

Ферма в Энциклопедическом словаре:

Ферма — (Fermat) Пьер (1601-65) — французский математик, один из создателейаналитической геометрии и теории чисел (теоремы Ферма). Труды по теориивероятностей, исчислению бесконечно малых и оптике (принцип Ферма).

---

(франц. ferme — от лат. firmus — прочный), в строительной механике -геометрически неизменяемая стержневая система, у которой все узлыпринимаются при расчете шарнирными. Металлические, железобетонные,деревянные и комбинированные фермы применяют в покрытиях зданий, мостах идр.

Значение слова Ферма по словарю Ушакова:

ФЕРМА
фермы, ж. (фр. ferme) (с.-х.). 1. Хозяйственное предприятие, занимающееся какой-н. специальной отраслью сельского хозяйства. Животноводческая ферма. Молочная ферма. 2. В капиталистических государствах — частное сельскохозяйственное предприятие на собственном или арендуемом участке, хутор.

---

ФЕРМА
фермы, ж. (фр. ferme) (тех.). Сооружение, представляющее собой конструкцию из стержней, брусьев. Стальная ферма. Арочная ферма. Балочная ферма. Стропильная ферма. Мостовые фермы.

Значение слова Ферма по словарю Даля:

Ферма
ж. франц. заимка сиб. хутор южн. мыза петерб. особенно для скота. Фермер, хозяин или съемщик, кортомщик хутора.

Значение слова Ферма по словарю Брокгауза и Ефрона:

Ферма (Пьер Fermat) — знаменитый французский математик (1601—1665). Сын торговца. изучил законоведение и с 1631 г. до конца жизни был советником Тулузского парламента. Научные сведения Ф., и притом не только в области наук математических, поражали его соотечественников разносторонностью и глубиной. Владея южно-европейскими языками и глубоко изучив латинский и греческий, Ф. был гуманистом и поэтом, писавшим французские и латинские стихи. Из древних писателей он комментировал Атенея, Полифнуса, Синезиуса, Теова Смирнского и Фронтина, исправил текст Секста Эмпирика. Изучив творения Бакона Веруламского, он не только проник в их смысл глубже Декарта, но в отношении экспериментального метода он пошел даже далее самого их автора, так как не ограничился одним теоретическим знакомством с методом, но в ряде опытов по предмету экспериментальной механики дал ему непосредственное приложение к действительности. При жизни Ф. о его математических работах стало известно главным образом через посредство обширной переписки, которую он вел с другими учеными, преимущественно с Мерсеннем, Робервалем, Паскалями, Этьенном и Блезом, Декартом, Френиклем, Каркави, Гассенди, Сенье, Булльо, Дигби, Клерселье, Лалувером и Гюйгенсом. Сам Ф. напечатал только два свои произведения: геометрическую диссертацию «De linearum curvarum cum lineis rectis comparatione» (Тулуза, 1660), вместе с приложением к ней, и анонимную статью без заглавия, вошедшую в качестве «первой части второго прибавления» в состав книги иезуита Лалувера «Veterum Geometria p r omota in septem de Cycloide libris, et in duabus adjectis Appendicihus» (Тулуза, 1660). Из переписки Ф. при его жизни в печать проникли, кроме нескольких отрывков, письмо к Гассенди, помешенное в VI томе «Собрания сочинений» последнего (Лион, 1658), и девять писем, напечатанных английским математиком Валлисом в его издании «Commercium epistolicum de Quaestionibus quibusdam Mathematicis nuper habitum inter nobilissimos Viros etc.» (Оксфорд, 1658). Этих работ Ф. оказалось, однако же, вполне достаточно для единогласного его признания современниками одним из выдающихся математиков. Крупную заслугу Ф. перед наукой видят обыкновенно во введении им бесконечно малой величины в аналитическую геометрию, подобно тому, как это несколько ранее было сделано Кеплером в отношении геометрия древних. Он совершил этот важный шаг в своих относящихся к 1629 г. работах о наибольших и наименьших величинах — работах, открывших собой тот из важнейших рядов исследований Ф., который является одним из самых крупных звеньев в истории развития не только высшего анализа вообще, но и анализа бесконечно малых в частности. Метод Ф. нахождения наибольших и наименьших величин состоял в следующем. В выражение, переходящее в свое наибольшее или наименьшее значение, вместо неизвестного x вставляется сумма двух неизвестных x + е. Полученная через эту подстановку новая форма выражения приравнивается его первоначальной форме, чем и порождается взгляд на неизвестное e как на величину крайне малую. В найденном таким образом уравнении опускаются содержащиеся в обеих его частях одинаковые члены, оставшиеся делятся на e, и те из них, в которых e удержалось и после деления, опускаются совсем. В результате получается уравнение, доставляющее наибольшее или наименьшее значение неизвестного x. В терминах современного знакоположения весь этот процесс может быть представлен в виде или Изложенный первоначально в статье «Methodus ad disquirendam maximum et minimam», этот метод лег в основание и двух следовавших за ним, также очень важных работ Ф. в той же области, именно способа проведения касательных к кривым и приема определения центра тяжести параболоида вращения. Из них первый сделался известным в 1642 г. из «Дополнения» к «Cursus mathemаtici» Геригона, а второй — из статьи «Centrum gravitatis paraboilici conoidis, ex eadem methode», пересланной в 1638 г. через Мерсення Робервалю. В ряде исследований Ф. по предмету высшего анализа все указанные до сих пор могут быть обозначены, следуя новейшей терминологии, одним общим названием приложений дифференциального исчисления. Что касается остальных исследований из принадлежащих тому же ряду, то они также могут быть соединены в одну группу, общая характеристика которой вполне исчерпывается термином приложения интегрального исчисления. Членами этой группы были квадратуры, кубатуры и ректификации. Первое сделавшееся известным изложение результатов работ Ф. по предмету квадратур и кубатур представляет упомянутая уже выше статья («Ad bon. Cavalierii quaestiones responsa»), посланная автором в 1644 г. Кавальери через посредство Мерсення. Предмет ее состоит в не сопровождаемом доказательствами изложении данных автором решений вопросов Кавальери. Она содержит в себе квадратуры парабол различных порядков, кубатуры происходящих от них тел вращения и определения центров тяжести последних. В гораздо более подробном виде знакомит с теми же работами Ф. другое, по-видимому, более позднее сочинение, напечатанное после смерти автора: «De aequationum localium transmutatione et emendatione ad multimodam curvilineorum inter se vel c um rectilineis comparationem, cui annectitur proportionis geometricae in quadrandis infinitis parabolis et hyperbolis usus». Что касается найденного Ф. способа ректификации, или выпрямления, кривых, то он изложен в его уже упомянутой выше диссертации «De l inearum curvarum cum lineis rectis comparatione». He менее важными по своим последствиям, чем работы по высшему анализу, и едва ли не более блестящими по своей глубине и остроумию были результаты исследований Ф. в области теории чисел. Особого посвященного им сочинения автор не оставил, но сохранились заметки, рассеянные, и по большей части без доказательств, в письмах Ф. и в особенности на полях принадлежащего автору экземпляра сочинений Диофанта в издании Баше де Мезириака. В числе заметок на экземпляре сочинений Диофанта находилось важнейшее из открытий Ф. в области теории чисел — теорема о невозможности разложения какой-нибудь степени, за единственным исключением квадрата, на две такие же степени. Знаменитое предложение, известное под именем теоремы Ф. и выражаемое сравнением в котором p есть первоначальное число, а а есть число, не делящееся на p, было дано Ф. в письме к неизвестному лицу от 18 октября 1640 г. Доказательство первой из этих двух теорем было найдено позднейшими математиками (Эйлером, Дирикле, Куммером) только с большим трудом и притом в формах, которыми сам Ф. никак не мог пользоваться. Из других работ Ф. остается упомянуть: 1) о его занятиях решением некоторых вопросов теории вероятностей, вызванных или поставленных перепиской с Блезом Паскалем. 2) о попытках восстановления некоторых из утраченных произведений древних греческих математиков и, наконец, 3) о его спорах с Декартом по поводу метода определения наибольших и наименьших величин и по вопросам диоптрики. Сочинениями, которые Ф. намеревался восстановить, были «Поризмы» Эвклида и «Плоские места» Аполлония Пергейского. Поводом ко второму из вышеупомянутых споров Ф. с Декартом был найденный последним закон преломления. Ф. находил сомнительным утверждение противника, что свет при прохождении через тело встречает тем менее сопротивления, чем это тело плотнее. Также спорил он и против утверждения, что отражение света может быть объяснено отскакиванием неупругих световых частиц. Позднее, после смерти Декарта, спор по тем же предметам Ф. продолжал с его учеником Клерселье. Собрание математических сочинений и писем Ф. было издано в, первый раз его сыном Самюелем в 1679 г.: «Varia opera mathematica D. Petri de Fermat, Senatoris tolosani. Accesserunt selectae quaedam ejusdem Epistol ae, vel ad ipsum a plerisque doctissimis vins Gallic&egrave., Latm&egrave., vel Italic&egrave., de rebus ad Mathematicis disciplinas aut Physicam pertinentibus scriptae» (Тулуза). В 1861 г. в Берлине появилась перепечатка этого издания, сделанная Фридлендером. Новое, более полное и совершенное собрание сочинений Ф. было издано в Париже в трех томах, под заглавием «Oeuvres de Fermat, publi &eacute.es par les soins de P. Tannery et Ch. Henry» (1896). &#914.. &#914.. Бобынин.

Определение слова «Ферма» по БСЭ:

Ферма — Ферма (Fermat)
Пьер (17.8.1601, Бомон-де-Ломань, — 12.1.1665, Кастр), французский математик. По профессии юрист: с 1631 был советником парламента в Тулузе. Автор ряда выдающихся работ, большинство из которых было издано после смерти Ф. его сыном, —
«Различные сочинения» (1679). при жизни Ф. полученные им результаты становились известны учёным благодаря переписке и личному общению.
Ф. является одним из создателей теории чисел, где с его именем связаны 2 знаменитые теоремы: Ферма великая теорема и Ферма малая теорема. В области геометрии Ф. в более систематической форме, чем Р. Декарт, развил метод координат, дав уравнения прямой и линий второго порядка и наметив доказательство положения о том, что все кривые второго порядка — конического сечения. В области метода бесконечно малых систематически изучил процесс дифференцирования, дал общий закон дифференцирования степени и применил этот закон к дифференцированию дробных степеней.
В подготовке современных методов дифференциального исчисления большое значение имело создание им правила нахождения экстремумов. Ф. дал общее доказательство правильности закона интегрирования степени, подмеченного на частных случаях уже ранее. Он распространил его и на случай дробных и отрицательных степеней. В трудах Ф., таким образом, получили систематическое развитие оба основных процесса метода бесконечно малых, однако он, как и его современники, прошёл мимо связи между операциями дифференцирования и интегрирования. Эта связь была установлена несколько позднее (в систематической форме) Г. Лейбницем и И. Ньютоном. Своими работами Ф. оказал большое влияние на дальнейшее развитие математики. В области физики с именем Ф. связано установление основного принципа геометрической оптики (см. Ферма принцип).
Соч.: CEuvres, t. 1-4, P., 1891-1912.
Лит.: Бурбаки Н., Элементы математики, [кн. 8]. Очерки по истории математики, пер. с франц., М., 1963 [лит.]. История математики с древнейших времён до начала XIX столетия, т, 2, М., 1970.
П. Ферма.

---

Ферма — Ферма (франц. ferme, от лат. firmus — крепкий, прочный)
несущая конструкция, состоящая из прямолинейных стержней, узловые соединения которых при расчёте условно принимаются шарнирными. Ф. применяют главным образом в строительстве (покрытия зданий, пролётные строения мостов, мачты, опоры линий электропередачи, гидротехнические затворы и др.), а также в качестве несущих конструкций машин и механизмов. По виду материала различают металлические, железобетонные, деревянные и комбинированные (например, металлодеревянные) Ф. Тип Ф. и её очертания (рис.) определяются назначением здания или сооружения, видом покрытия, способом опирания Ф. и т.д. Узлы Ф., хотя и считаются шарнирными, практически обладают той или иной степенью жёсткости. При проектировании Ф., как правило, обеспечивается узловое приложение внешней нагрузки (например, прогоны покрытия здания опираются на Ф. в узлах верхнего пояса, балки подвесных кранов крепятся к узлам нижнего пояса и т.д.).
Допущения о шарнирном соединении узлов и узловом приложении нагрузки позволяют учитывать при расчёте Ф. только осевые продольные усилия в стержнях (при этом в поперечных сечениях стержней возникают равномерно-распределённые напряжения, позволяющие наиболее эффективно использовать материал). Усилия в стержнях статически определимых плоских Ф. (см. Статически определимая система) определяют из уравнений статики, пространственных — как правило, путём расчленения на плоские. Статически неопределимые Ф. (см. Статически неопределимая система) рассчитывают при помощи уравнений метода сил (см. Строительная механика), в которых коэффициенты при неизвестных (перемещения) определяют с учётом действия только нормальных усилий в элементах Ф. При расчёте Ф. на подвижные нагрузки используют т. н. линии влияния.
Лит. см. при статьях Строительная механика, Металлические конструкции, Железобетонные конструкции и изделия, Деревянные конструкции.
Л. В. Касабьян.
Классификация ферм по типам решётки: а — балочная раскосная. б — балочная с треугольной решёткой. в — балочно-консольная с треугольной решёткой и дополнительными стойками. г — консольная полураскосная. д — консольная двухраскосная. е — балочная двухрешётчатая. 1 — верхний пояс. 2 — нижний пояс. 3 — раскос. 4 — стойка.

---

xn—-7sbbh7akdldfh0ai3n.xn--p1ai

Что такое ферма | Все о ремонте и строительстве

Объяснить попробую настолько просто, насколько смогу.

Приложение вертикальной силы к балке обычного прямоугольного сечения приводит к ее прогибу (рис. 118). При этом в верхней части сечения возникают внутренние напряжения сжатия δ_сж, а в нижней — растяжения δ_рас. Их можно изобразить в виде схемы по которой видно, что своих максимальных значений напряжения достигают на верхней и нижней границах сечения балки, а в центре оно равно нулю, то есть прямоугольное сечение балки работает неравномерно. Если удалить из него неработающие области получим двутавровое сечение. Двутавр — это главный строительный профиль. От деления двутаврового сечения получаются швеллеры, тавры и уголки, которые в обратной сборке могут образовать исходный двутавр, короб или крест.

Рис. 118. Ферма

Продолжим дальше удалять из балки «лишний» материал, уменьшать ее вес без потери несущей способности. Вырежем в вертикальной перегородке двутавровой балки отверстия максимально возможных размеров. Получившаяся «дырявая» балка — это прообраз фермы, в которой верхняя и нижняя часть называются поясами, а стержни их связывающие, стойками или подвесками (зависит от того оперта балка или подвешена). Понятно, что такой прообраз фермы можно изготовить не удалением «лишнего» материала из тела балки, а более простым путем сколачивания брусков и досок или сваривания металлических профилей.

При изготовлении нашей фермы из брусков в итоге получаем конструкцию пригодную и равную по несущей способности первоначальной балке прямоугольного сечения, но неустойчивую к боковым нагрузкам. Ведь по сути мы получили лестницу-стремянку, которую можно легко разрушить если приложить к ней горизонтальную силу. Устраним этот недостаток введением в конструкцию диагональных связей. Здесь они называются раскосами, а стойки (подвески) лучше называть одним словом шпренгель (распорка). Расстояния между узлами фермы называются панелями.

Главный недостаток обычной балки — большой прогиб от нагрузки. В строительных конструкциях сечение балки зачастую принимается не по несущей способности, а по прогибу. Иными словами, для сооружений используется такое сечения балки, которое не допускает большого прогиба, но сама балка при этом способна нести гораздо большую нагрузку, чем на нее возлагают. Имеем нерациональное использование материала балки. Уменьшение прогиба балки достигается увеличением ее высоты. Например, если взять обычную ученическую линейку, то можно легко убедиться, что она хорошо гнется при расположении плашмя и плохо — если ребром. Однако с увеличением высоты балки увеличивается её вес, и балка начинает прогибаться даже под собственным весом без внешней нагрузки. Вот тут и приходит на помощь облегченная «дырявая» балка — ферма, которую можно изготовить большой высоты без существенного увеличения веса.

Почему для описания фермы в качестве исходника взята балка, а не висячая стропильная система или какая-то другая конструкция крыши?  Потому что не хочется привязывать фермы только к конструкциям крыш так как они широко используются в строительстве и машиностроении, а хочется закрепить понимание того, что ферма в целом работает так же, как балка. Например, при опирании на две опоры и загружении сверху в ее верхнем поясе возникают внутренние сжимающие напряжения, а в нижнем — растягивающие, она не передает распора на стены.

Фермы нагружают распределённой нагрузкой или сосредоточенными силами (рис. 119).

• Если строительную конструкцию разработать таким образом, что сосредоточенные силы будут приложены исключительно в узлах ферм, то в элементах фермы (поясах, шпренгелях и раскосах) не будет возникать изгибающих моментов. Они будут работать только на сжатие и растяжение, что позволяет уменьшать сечение этих элементов до необходимого минимума. Сами фермы при этом можно изготавливать из коротких элементов длиной от узла до узла, а узлы изготавливать по шарнирной схеме. Ферма — геометрически неизменяемая стержневая система с шарнирными узлами. Такие фермы часто встречаются в металлическом исполнении. Для деревянных ферм обычно используются схемы с изготовлением верхних и нижних поясов не короткими досками (от узла до узла), а длинными, во всю доступную длину. В этом случае пояса ферм не соединяются шарнирами в каждом узле, а опираются на них и подвешиваются к ним. Хотя и деревянную ферму тоже можно собрать из коротких дощечек. Главное, что нужно понять, нагрузка — приложенная в узлах в виде сосредоточенных сил, не будет изгибать элементы фермы.

• Если на ферму будет действовать равномерно распределенная нагрузка, то в стержнях верхнего пояса появится изгибающий момент дополнительно к сжимающим и растягивающим напряжениям. Изгибающий момент достигает своего максимального значения в середине каждого стержня пояса панели фермы при шарнирах врезанных в узлы, либо на опорах — при шарнирах, расположенных под/над поясом фермы. Соответственно сечение стержней фермы будет большим, чем если бы ферма была нагружена точечными силами в узлах.

В использовании схемы нагружения кроется главное преимущество ферм. При одной и той же величине внешней нагрузки правильное ее распределение на ферму дает преимущество в экономии материала.

Рис. 119. Различие работы ферм взависимости от способа загружения и изготовления

Фермы нужной длины (пролета) к которым будет приложена точечная нагрузка в узлах можно изготавливать из коротких элементов длиной от узла до узла.

Фермы, на которые будет действовать равномерно распределенная нагрузка тоже можно изготавливать из коротких элементов если узлы фермы будут шарнирами; и из длинных если шарниры будут под/над поясами.

Обычно для крыш используются деревянные фермы, сделанные из длинных досок. Так как перекрываемые пролеты бывают больше, чем позволяет длина досок, фермы делают из двух частей. Стыкуя их примерно на расстоянии 1/5 длины панелей, то есть там, где изгибающий момент стремится нулю.

 

ostroykevse.com

ферма — это… Что такое ферма?

ферма́та — фермата …   Русское словесное ударение

ФЕРМА — плоская конструкция, состоящая из соединенных между собой отдельных стержней или дисков, перекрывающая отверстие между опорами и передающая на последние воспринимаемую ею нагрузку. Арочная ферма Изготовляется из металла, дерева или железобетона.… …   Технический железнодорожный словарь

ФЕРМА — (фр. ferme, от лат. firme крепко, прочно). 1) арендуемый деревенский дом, при котором есть сад, скотный двор, а иногда и пахотная земля; то же, что мыза, хутор. 2) в Петербурге молочная ферма есть просто приют для дойных коров, откуда отпускают… …   Словарь иностранных слов русского языка

ФЕРМА — • ФЕРМА (Fermat) Пьер де (1601 65), французский математик. Вместе с Блезом ПАСКАЛЕМ сформулировал теорию вероятности и, доказав, что свет перемещается по самой короткой оптической траектории (принцип Ферма), стал основателем геометрической оптики …   Научно-технический энциклопедический словарь

ФЕРМА — 1. ФЕРМА1, фермы, жен. (франц. ferme) (с. х.). 1. Хозяйственное предприятие, занимающееся какой нибудь специальной отраслью сельского хозяйства. Животноводческая ферма. Молочная ферма. 2. В капиталистических государствах частное… …   Толковый словарь Ушакова

ФЕРМА — 1. ФЕРМА1, фермы, жен. (франц. ferme) (с. х.). 1. Хозяйственное предприятие, занимающееся какой нибудь специальной отраслью сельского хозяйства. Животноводческая ферма. Молочная ферма. 2. В капиталистических государствах частное… …   Толковый словарь Ушакова

Ферма — частное сельскохозяйственное предприятие, принадлежащее фермеру и ведущееся им на собственной или арендованной земле. По английски: Farm Синонимы: Фермерское хозяйство См. также: Сельскохозяйственные предприятия Финансовый словарь Финам …   Финансовый словарь

ферма — ранчо, усадьба, хутор; умет, племхоз, фольварк, хозяйство, консоль Словарь русских синонимов. ферма сущ., кол во синонимов: 24 • виброферма (1) • …   Словарь синонимов

ферма —     ФЕРМА, хозяйство …   Словарь-тезаурус синонимов русской речи

ферма — ферма; колхоз фермани колхозная ферма …   Нанайско-русский словарь

Ферма — – плоская стержневая несущая конструкция. [Терминологический словарь по бетону и железобетону. ФГУП «НИЦ «Строительство» НИИЖБ им. А. А. Гвоздева, Москва, 2007 г. 110 стр.] Ферма – несущая стержневая конструкция, как правило… …   Энциклопедия терминов, определений и пояснений строительных материалов

dic.academic.ru