Институт интеллектуальных кибернетических систем | Приемная комиссия НИЯУ МИФИ
Внимание! В период с апреля по май онлайн-консультации в дискорде проходят по понедельникам и четвергам (16:00-18:00) и в субботу 12:00-13:00.
Цель: Подготовка кадров, способных противостоять современным угрозам и вызовам, обладающих знаниями и компетенциями в области кибернетики, информационной и финансовой безопасности для решения задач разработки базового программного обеспечения, повышения защищенности критически важных информационных систем и противодействия финансированию терроризма и отмыванию денег.
Общая информация
Институт занимается исследованиями и инновационными разработками в области кибернетики, информационной и финансовой безопасности. Преимуществами института являются: подготовка кадров, обладающих актуальными компетенциями в области кибернетики, информационной и финансовой безопасности для профессионального решения задач построения защищенных информационных систем и разработки программного обеспечения; обучение технологиям проактивной киберзащиты, в том числе принципам построения адаптирующихся к быстро изменяющейся среде интеллектуальных агентов кибербезопасности и высокопроизводительных защищенных распределенных инфраструктур хранения и обработки данных, повышающих скорость реакции на киберугрозы и эффективность выявления незаконных финансовых операций; вовлечение в исследовательские работы в области робототехники и киберфизических систем.
При институте функционируют 4 малых инновационных предприятия.
Основные сферы трудоустройства выпускников: государственная служба, банковская сфера, финансовая сфера, аудит, IT-сфера, информационная безопасность.
Образовательные программы
| Бакалавриат | |
|---|---|
| Код | Направление |
| 09.03.01 | Информатика и вычислительная техника |
| 09.03.04 | Программная инженерия |
| 10.03.01 | Информационная безопасность |
| Специалитет | |
| 09.05.01 | Применение и эксплуатация автоматизированных систем специального назначения |
| Магистратура | |
| 09.04.01 | Информатика и вычислительная техника |
09. 04.04 | Программная инженерия |
| 10.04.01 | Информационная безопасность |
| Аспирантура | |
| 09.06.01 | Информатика и вычислительная техника |
| 10.06.01 | Информационная безопасность |
Кафедры
12 Компьютерные системы и технологии
22 Кибернетика
41 Защита информации
42 Криптология и кибербезопасность
43 Стратегические информационные исследования
44 Информационная безопасность банковских систем
65 Анализ конкурентных систем
Технологический потенциал
-Суперкомпьютер «Басов»
-Суперкомпьютер «Черенков»
-20 современных компьютерных классов для обучения студентов
-5 специализированных лабораторий по информационной безопасности
-6 студенческих конструкторских исследовательских бюро, оснащенных высокопроизводительным научным оборудованием
-Учебно-производственный комплекс: мелкосерийное производство высокотехнологичной продукции с автоматизированной системой управления
-Лабораторный стенд от компании National Instruments на базе аппаратно-программного LabView для изучения принципов разработки электронных устройств
-Стенды для изучения приемов разработки встраиваемых устройств на базе микроконтроллеров
-3 кластера для изучения методов параллельного программирования и построения высоконагруженных систем
-Лабораторный комплекс для изучения сетевых телекоммуникационных технологий на базе оборудования CISCO
С более подробной информацией можно ознакомиться на сайте и в справочных материалах.
Институт интеллектуальных кибернетических систем (ИИКС)
Кафедры и подразделения:
12 Компьютерные системы и технологии
22 Кибернетика
42 Криптология и кибербезопасность
43 Стратегические информационные исследования
44 Информационная безопасность банковских систем
65 Анализ конкурентных систем
227 Учебно-научная лаборатория «Научная визуализация»
Цель создания лаборатории: Учебно-научная лаборатория занимается вопросами разработки и практического использования инструментальных средств и методов компьютерной визуализации научных данных, а также подготовкой специалистов в этой области
425 Научно-исследовательская лаборатория «Когнитивные архитектуры и семантические технологии»
Цель создания лаборатории: разработки и исследования в области когнитивных архитектур и семантических технологий
575.
1 Учебный отдел института интеллектуальных кибернетических систем
415 Отделение интеллектуальных кибернетических систем офиса образовательных программ
578 Аттестационно-испытательный центр информационной безопасности и систем защиты информации
Отделение интеллектуальных кибернетических систем ИАТЭ
Международная лаборатория Кудряшова Н.А. (см. ниже)
Цель создания лаборатории: исследования в области нелинейной математической физики и математического моделирования
- Гибридные суперкомпьютерные технологии
- Робототехника
- Нейротехнологии и когнитивные архитектуры
- Интеллектуальные системы и технологии
- Программная инженерия и информационная поддержка разработки производства наукоемких изделий и технологий
- Фундаментальные основы информационных технологий
- Центр высокопроизводительных вычислений
- Кибербезопасность научно-образовательных объектов информатизации
- Аттестация объектов информатизации по требованиям безопасности информации
- Когнитивные архитектуры и семантические технологии
Общая информация | ИАТЭ НИЯУ «МИФИ»
Строка навигации
- Главная
- Образование
- Институты
- Институт интеллектуальных кибернетических систем
Общая информация
СТРАТЕГИЧЕСКАЯ ЦЕЛЬ ИИКС — ГЛОБАЛЬНОЕ ЛИДЕРСТВО В ПОДГОТОВКЕ КАДРОВ В ОБЛАСТИ КИБЕРНЕТИКИ, МАШИННОГО ИНТЕЛЛЕКТА, ИНФОРМАЦИОННОЙ И ФИНАНСОВОЙ БЕЗОПАСНОСТИ!!!
ОСНОВНЫЕ ПРИНЦИПЫ ОБРАЗОВАТЕЛЬНЫХ ПРОГРАММ ИИКС
- «Старт» со школьной скамьи (работа со школьниками, Предуниверситарии, летние IT-школы)
- Единое образовательное пространство (Москва, Обнинск)
- Универсальность дисциплин базового цикла
- Гибкость образовательных траекторий
- Модульность специальных дисциплин
- Привлечение ведущих IT-специалистов, национальных и мировых лидеров
- Развитие инновационной инфраструктуры (Программы «Умник», «Старт», Хакатоны, олимпиады, создание инновационных малых предприятий)
- Внедрение передовых образовательных программ в соответствии с современными стандартами (в т.
К ПРИОРИТЕТНЫМ НАПРАВЛЕНИЯМ ОБРАЗОВАТЕЛЬНЫХ ПРОГРАММ ИИКС ОТНОСЯТСЯ:
- Искусственный интеллект и машинное обучение
- Нечеткие системы и мягкие вычисления
- Высокопроизводительные вычисления
- Облачные вычисления
- Блокчейн-технологии
- Цифровая экономика
- Технология «Умный дом»
- Большие данные (Big Data)
- Интернет вещей
- Компьютерное зрение
- Нейросенсорика
- Java- и Web-технологии
- Новые принципы построения компьютерных архитектур
- Корпоративные информационные системы
- Геоинформационные системы
- Робототехника
- Методы и системы поддержки принятия решений
- Беспроводные технологии
- Параллельное программирование
- Моделирование и анализ поведения сложных систем
В ИИКС обучаются более 300 студентов(из них 80 обучаются в магистратуре).
Занятия проводятся высокопрофессиональными преподавательскими кадрами, активно ведущими исследования в рамках научных лабораторий отделения. Проводятся исследования в рамках следующих направлений: обработка больших данных, искусственный интеллект и машинное обучение, перспективные высокопроизводительные архитектуры, моделирование сложных систем. Базами практик, индивидуальных и проектных исследовательских работ студентов ИИКС, наряду с научными лабораториями, являются ведущие научные центры наукограда ОБНИНСК, предприятия IT-кластера Калужской области, академические и проектные институты Москвы. К процессу обучения привлекаются ведущие IT-компании России, специалисты которых читают студентам лекции и проводят практические занятия в рамках учебных курсов и соревнований.
МИФИ запускает программу по безопасности компьютерных систем
https://na.ria.ru/20210726/mifi-1742564239.html
МИФИ запускает программу по безопасности компьютерных систем
МИФИ запускает программу по безопасности компьютерных систем — РИА Новости, 26.
07.2021
МИФИ запускает программу по безопасности компьютерных систем
Национальный исследовательский ядерный университет «МИФИ» (НИЯУ МИФИ) запускает новую программу бакалавриата «Безопасность компьютерных систем (Объекты… РИА Новости, 26.07.2021
2021-07-26T09:00
2021-07-26T09:00
2021-07-26T09:00
общество
национальный исследовательский ядерный университет «мифи»
приемная кампания в вузы
навигатор абитуриента
кем стать
/html/head/meta[@name=’og:title’]/@content
/html/head/meta[@name=’og:description’]/@content
https://cdnn21.img.ria.ru/images/07e5/05/1f/1734881429_0:329:2951:1989_1920x0_80_0_0_10320d209f651f56fa5e24414c823278.jpg
МОСКВА, 26 июл — РИА Новости. Национальный исследовательский ядерный университет «МИФИ» (НИЯУ МИФИ) запускает новую программу бакалавриата «Безопасность компьютерных систем (Объекты критической информационной инфраструктуры)», сообщили в пресс-службе вуза.Наукоемкие информационные технологии и информационно-технологические системы стремительно развиваются, расширяются области их применения, появляются новые способы и средства распределенного хранения, обработки и передачи информации.
Как отметили в пресс-службе вуза, в условиях появления новых технологичных угроз информационной безопасности остро встает вопрос подготовки высококвалифицированных кадров.Новая программа бакалавриата НИЯУ МИФИ «Безопасность компьютерных систем (Объекты критической информационной инфраструктуры)» будет существенно отличаться от всех других программ, связанных с обеспечением информационной безопасности, рассказал директор института интеллектуальных кибернетических система НИЯУ МИФИ Валентин Климов.Климов также отметил, что особое внимание будет уделено защите информационно-вычислительных сетей и систем, криптографическим методам, архитектуре безопасности ЛВС и Интернет-сети, компьютерной криминалистике, тестированию на проникновение и анализу защищенности информационно-технологических систем. Также студенты прослушают специализированные курсы по дискретной математике, теории вероятностей и математической статистике, теории информации и другим математическим дисциплинам. «Мы уверены, что сумеем подготовить высококлассных специалистов, востребованных ведущими высокотехнологичными компаниями», — отметила проректор НИЯУ МИФИ Елена Весна.
По ее словам, среди преподавателей новой программы будут и опытные практики в области обеспечения информационной безопасности, и молодые специалисты из числа призеров международной олимпиады по криптографии «NSUCRYPTO» и других специальных конкурсов.
https://na.ria.ru/20210723/mifi-1742006730.html
https://na.ria.ru/20210723/mifi-1742006730.html
https://na.ria.ru/20210407/vuzy-1603408442.html
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
2021
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
Новости
ru-RU
https://na.ria.ru/docs/about/copyright.html
https://xn--c1acbl2abdlkab1og.xn--p1ai/
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.
xn--p1ai/awards/
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
общество, национальный исследовательский ядерный университет «мифи», приемная кампания в вузы, навигатор абитуриента, кем стать
МОСКВА, 26 июл — РИА Новости. Национальный исследовательский ядерный университет «МИФИ» (НИЯУ МИФИ) запускает новую программу бакалавриата «Безопасность компьютерных систем (Объекты критической информационной инфраструктуры)», сообщили в пресс-службе вуза.Наукоемкие информационные технологии и информационно-технологические системы стремительно развиваются, расширяются области их применения, появляются новые способы и средства распределенного хранения, обработки и передачи информации.
Как отметили в пресс-службе вуза, в условиях появления новых технологичных угроз информационной безопасности остро встает вопрос подготовки высококвалифицированных кадров.
23 июля 2021, 09:00
Новые программы обучения лазерным технологиям запустили в МИФИНовая программа бакалавриата НИЯУ МИФИ «Безопасность компьютерных систем (Объекты критической информационной инфраструктуры)» будет существенно отличаться от всех других программ, связанных с обеспечением информационной безопасности, рассказал директор института интеллектуальных кибернетических система НИЯУ МИФИ Валентин Климов.
«Мы сделали акцент на фундаментальную математическую подготовку, изучение теоретических основ кибербезопасности и углубленное освоение современных информационных технологий, необходимых для решения задач защиты объектов критической информационной инфраструктуры. Выпускники программы будут востребованы в высокотехнологичных компаниях, где смогут разрабатывать математические модели кибербезопасности, обеспечивать безопасность и защиту данных в сфере эксплуатации комплексов программных и программно-аппаратных технических средств», — прокомментировал он.
Климов также отметил, что особое внимание будет уделено защите информационно-вычислительных сетей и систем, криптографическим методам, архитектуре безопасности ЛВС и Интернет-сети, компьютерной криминалистике, тестированию на проникновение и анализу защищенности информационно-технологических систем.
Также студенты прослушают специализированные курсы по дискретной математике, теории вероятностей и математической статистике, теории информации и другим математическим дисциплинам.
23 июля 2021, 09:00
Новые программы обучения лазерным технологиям запустили в МИФИ«Мы уверены, что сумеем подготовить высококлассных специалистов, востребованных ведущими высокотехнологичными компаниями», — отметила проректор НИЯУ МИФИ Елена Весна.
По ее словам, среди преподавателей новой программы будут и опытные практики в области обеспечения информационной безопасности, и молодые специалисты из числа призеров международной олимпиады по криптографии «NSUCRYPTO» и других специальных конкурсов.
7 апреля 2021, 09:00
Профессии, зарплаты, вузы: навигатор абитуриента 2021Национальный исследовательский ядерный университет «МИФИ» (МИФИ): факультеты и кафедры
Инженерно-физический институт биомедицины НИЯУ МИФИ (ИФИБ)
Целью ИФИБ является подготовка высококвалифицированных специалистов в области инженерно-физических технологий для биомедицины, включая ядерную и трансляционную медицину, в интересах Российских научных центров, инновационных предприятий и клиник. ИФИБ объединил в своем составе кафедры НИЯУ МИФИ медицинского, биологического, химического, инженерного и IT-профилей, что позволяет готовить специалистов, обладающих знаниями и компетенциями на стыке этих областей.
Задачи ИФИБ:
Проведение научных исследований с привлечением студентов и аспирантов в области современных биомедицинских технологий для разработки методов ранней диагностики и адресного лечения онкологических и других социально значимых заболеваний;
Подготовка на базе научных исследований и инженерно-физических разработок высококвалифицированных кадров для работы на современном биомедицинском оборудовании;
Использование результатов научных исследований для создания новых медицинских технологий, патентная и организационная поддержка новых стартапов, коммерциализация научных результатов;
Формирование на основе ИФИБ Центра трансляционной медицины для быстрого внедрения новых разработок.
Образование в ИФИБ основано на использовании современных принципов обучения: гибкие образовательные программы, модульная структура образовательных программ, индивидуальные траектории, практикоориентированность.
Уникальность образовательных программ ИФИБ:
Научная стратегия ИФИБ нацелена на достижение синергетического эффекта от объединения современных технологий нанобиоинженерии, бионанофотоники и технологий ядерной медицины. Подготовка кадров, которые будут обладать необходимыми знаниями и компетенциями для работы в этих динамично развивающихся областях, быстрой трансляции этих знаний в медицину, основана на уникальных образовательных программах, обладающих гибкостью к появляющимся новым научным достижениям и внедряющих их в образовательный процесс.
Набор образовательных программ для подготовки специалистов в биомедицине, включая ядерную медицину (особенно на высших уровнях подготовки – в магистратуре, аспирантуре) должен, с одной стороны, давать базовые знания и навыки в соответствующих научных областях, с другой – оперативно включать передовые достижения в учебный процесс.
Такая динамичность достигается в ИФИБ путем создания новых образовательных программ на модульной основе и регулярной модернизации существующих программ, а также создания совместных образовательных программ с ведущими зарубежными университетами.
Особенности учебного процесса ИФИБ:
- Привлечение студентов к научной деятельности в процессе обучения
- Привлечение к чтению лекций ведущих зарубежных профессоров
- Стажировки студентов в зарубежных университетах–партнерах
- Регулярное проведение летних и зимних международных молодежных научных школ
Более полную информацию об ИФИБ Вы сможете найти на странице института ( http://physbio.mephi.ru/).
ИФЭБ и ИИКС НИЯУ МИФИ провели совместный День открытых дверей
Детали события:
- Дата:
Вместе – продуктивнее! ИФЭБ и ИИКС НИЯУ МИФИ провели совместный День открытых дверей
Институт интеллектуальных кибернетических систем совместно с Институтом финансовой и экономической безопасности НИЯУ МИФИ провели День открытых дверей, который, как всегда, собрал в альма-матер неравнодушных абитуриентов и их родителей.
Программа мероприятия начиналась в актовом зале, где прозвучали приветственные слова и прошли выступления представителей институтов, приглашенных гостей-работодателей, ответственного секретаря приемной комиссии и представителя военной кафедры. Кроме того, в ходе Дня открытых дверей были награждены победители и призеры международной студенческой олимпиады по криптографии NSUCRYPTO.
Мероприятие открыл заместитель директора Института интеллектуальных кибернетических систем НИЯУ МИФИ Валентин Климов, он рассказал о подразделении, его истории и основных векторах развития. «Мы уделяем внимание всем ключевым мировым проблемам в области IT-технологий. В первую очередь, это проблема искусственного интеллекта, его развития, внедрения роботов, так называемой нейротехнологической революции. Мы должны обеспечить своевременный и достойный выход России на мировой уровень. Нас также интересует разработка умных домов, машин и всего, что работает без участия человека. Еще одно важное направление работы – информационная безопасность и борьба с киберпреступностью.
Наш институт создан на триаде: наука, безопасность, инновации. Мы стоим на пороге новых научных открытий и внедряем их в обучение, поэтому готовим востребованных и конкурентоспособных специалистов», – обозначил Валентин Климов.
Программу продолжила заместитель директора Института финансово-экономической безопасности НИЯУ МИФИ Анна Норкина. «ИФЭБ был создан более 12 лет назад для обеспечения кадровой потребности Федеральной службы по финансовому мониторингу и других спецслужб РФ. В задачи Финмониторинга входит два направления: противодействие финансированию терроризма и производства оружия массового уничтожения. Также мы сотрудничаем с другими большими компаниями и корпорациями. В зависимости от потребностей рынка мы вносим корректировки в учебный план, чтобы готовить адаптированных к современным условиям специалистов, которые будут востребованы на рынке труда», – подытожила Анна Норкина. Также заместитель директора ИФЭБ поблагодарила всех за интерес к мероприятию и пригласила на совместный День открытых дверей всех подразделений НИЯУ МИФИ, чтобы лучше почувствовать атмосферу вуза.
В рамках официальной части программы выступил представитель Росфинмониторинга Марина Чурищева. «Мы ждем студентов НИЯУ МИФИ у себя на практике и стажировках, это неоценимый опыт в сфере финансовых расследований. Мы хотим видеть у себя специалистов со знанием правовой базы, иностранных языков, умением работать с открытыми источниками, обладающих знаниями в IT-сфере, владением математики, а также с хорошими личностными характеристиками. Каждый год специалисты из НИЯУ МИФИ пополняют нашу команду. Например, выпускник НИЯУ МИФИ 2009 года несколько раз проходил у нас практику, затем попал к нам в команду, и в 2018 году он занял должность начальника управления. Это очень хорошая карьера, и своим примером этот молодой человек доказал, что все это возможно», – рассказала Марина Чурищева и пригласила гостей мероприятия на мастер-класс Федеральной службы по финансовому мониторингу «Сто дорог – одна твоя!»
Череду выступлений продолжила руководитель совместного проекта НИЯУ МИФИ и Mail.
ru Group Оксана Озерная. «Проект «Техноатом» создан, чтобы сократить разрыв в знаниях, которые преподаются в вузе и которые приобретаются непосредственно на работе. «Техноатом» существует уже два года, в рамках проекта ведущие специалисты Mail.ru Group приходят в НИЯУ МИФИ и преподают студентам различные языки программирования абсолютно бесплатно. Для того чтобы принять участие в проекте, нужно быть студентом НИЯУ МИФИ и пройти онлайн-отбор, затем вы сможете посещать занятия и по окончании курса получите соответствующий сертификат. С этим сертификатом вам начисляются дополнительные баллы при поступлении в магистратуру НИЯУ МИФИ, а также вы можете прийти на стажировку к нам в компанию. В прошлом году 37 студентов НИЯУ МИФИ прошли стажировку у нас», – рассказала Оксана Озерная и пригласила узнать больше информации о проекте «Техноатом» и стажировках в Mail.ru Group у стенда компании, который расположен в библиотеке.
Следующий блок выступлений был посвящен вопросам поступления.
Ответственный секретарь приемной комиссии Игорь Цветков представил результаты приема прошлого года: проходные баллы по направлениям, контрольные цифры приема, минимальные баллы для подачи документов. Он отметил, что в последние годы качество приема в университет неизменно повышается, о чем свидетельствует увеличение среднего балла ЕГЭ поступивших в НИЯУ МИФИ. Также Игорь Цветков обратил внимание на то, что прием документов в НИЯУ МИФИ начинается 15 июня, а более подробно с правилами приема можно ознакомиться на официальном сайте университета в разделе Приемной комиссии НИЯУ МИФИ.
Официальная часть Дня открытых дверей завершилась выступлением начальника военной кафедры, полковника Андрея Коростелева. В своей речи он отметил, что НИЯУ МИФИ активно участвует во всех проектах, которые Министерство обороны реализует в отношении студентов. Работа ведется по четырем большим направлениям. Первое – подготовка офицеров запаса в интересах высокотехнологичных подразделений МО РФ по смежным направлениям подготовки.
Второе – подготовка солдат и сержантов запаса. Третье направление касается студентов, которые не прошли обучение на военной кафедре. После окончания НИЯУ МИФИ они могут пройти срочную службу в научной роте. И четвертое – выпускники НИЯУ МИФИ крайне востребованы Министерством обороны РФ, как хорошо зарекомендовавшие себя специалисты.
После официальной части школьников пригласили в библиотеку, где им были предложены различные мастер-классы и выставочная экспозиция научных групп ИИКС и ИФЭБ. «Анализ информационной безопасности публичного Wi-Fi», «Инвестиции. Формирование бизнес-кейса», Технологии виртуальной реальности», «Анализ связей в социальной сети «Вконтакте», «Интернет вещей» – еще не весь перечень мастер-классов, которые проходили в этот день в НИЯУ МИФИ. Федеральная служба по финансовому мониторингу провела в рамках Дня открытых дверей два мастер-класса: «Сто дорог – одна твоя!» и «Финансовая разведка в современном мире».
Национальный исследовательский ядерный университет «МИФИ» — один из первых двух национальных исследовательских университетов России, образован 8 апреля 2009 года на базе Московского инженерно-физического института (государственного университета).
Историю ведёт от основанного в 1942 году Московского механического института боеприпасов (ММИБ). Занятия начались 1 января 1943 года. Первый адрес института — улица Кирова (сейчас Мясницкая), 21. Первым директором института стал Алексей Никитович Дыгерн. Первоначальной целью института ставилась подготовка специалистов для военных и атомных программ Советского Союза. В 1945 году переименован в Московский механический институт, а в 1953 году — в Московский инженерно-физический институт (МИФИ). С 1993 года — Московский государственный инженерно-физический институт (технический университет). С 2003 года — Московский инженерно-физический институт (государственный университет). На территории университета находится научно-исследовательский ядерный реактор бассейнового типа. Университет имеет тесные связи с Государственной корпорацией по атомной энергии «Росатом» и Международным агентством по атомной энергии. НИЯУ МИФИ служит площадкой для проведения всевозможных событий в мире науки. Ежегодно в вузе проводится научная сессия МИФИ. При поддержке партнёра вуза в области высоких технологий — корпорации Intel — начиная с 1997 года НИЯУ МИФИ открывает двери школьным талантам, организуя молодёжный конкурс «Юниор», включённый в структуру международного научно-инженерного конкурса Intel International Science and Engineering Fair. Участник Проекта 5-100.
|
Читайте в новом номере«Аккредитация в образовании» № 7 (123) 2020
Известный американский фантаст Роберт Асприн однажды написал: «Когда на носу кризис, не трать силы на овладение сведениями или умениями, которыми ты не обладаешь. Окапывайся, и управляйся с ним, как сможешь, с помощью того, что у тебя есть». Кризис уже наступил, и обойтись имеющимся инструментарием вряд ли получится. Как жить в новом, дивном мире и развивать потенциал – читайте в 123-м номере «АО».
|
Москва, Каширское ш., 31.
В 2009 году университет стал одним из победителей федерального конкурса на статус национального исследовательского университета и был переименован в Национальный исследовательский ядерный университет «МИФИ».
В Снежинском физико-техническом институте НИЯУ МИФИ (Челябинская область) ознакомиться с направлениями и специальностями, востребованными в атомной отрасли, школьникам предлагают действием – попробовав получить конкретный результат своими руками под руководством наставников-студентов из числа чемпионов и призеров WorldSkills.
Университет имеет тесные связи с Государственной корпорацией «Росатом» и Международным агентством по атомной энергии.
А.Руденко.
Национальный исследовательский ядерный университет МИФИ (Московский инженерно-физический институт): рейтинги, стоимость и подробности о курсах
История Национального исследовательского ядерного университета «МИФИ» (Московский инженерно-физический институт) началась с основания в 1942 году Московского механического института боеприпасов.
Позднее здесь был создан головной российский ядерный университет МИФИ, в его развитии и становлении принимали участие ведущие советские ученые, в том числе руководитель советского атомного проекта Игорь Курчатов.В МИФИ за всю его историю работали шесть нобелевских лауреатов — Николай Басов, Андрей Сахаров, Николай Семенов, Игорь Тамм, Илья Франк и Павел Черенков.
НИЯУ МИФИ сегодня — один из ведущих научно-исследовательских университетов России, готовящий инженеров и ученых более чем по 200 направлениям. К наиболее перспективным направлениям обучения относятся:
- Наноматериалы и нанотехнологии;
- Радиационные и лучевые технологии;
- Медицинская физика и ядерная медицина;
- Сверхпроводимость и управляемый термоядерный синтез;
- Экология и биофизика;
- Информационная безопасность.
Кроме того, в МИФИ обучаются будущие менеджеры, специалисты и аналитики в области менеджмента, инженерной экономики, ядерного права и международного научно-технического сотрудничества.
Программы МИФИ:
С 2014 года в университете реализуются стандарты инициативы CDIO по модернизации инженерной подготовки в высшей школе. Стандарты направлены на повышение квалификации следующего поколения выпускников инженерных специальностей, а также используются ведущими мировыми университетами, такими как Стэнфордский университет, Калифорнийский государственный университет и Массачусетский технологический институт.
Аккредитованы FEANI (Федерация национальных инженерных ассоциаций) и Агентством по аккредитации программ инженерного образования (АНО АПИО).
Выпускник, обучавшийся по аккредитованной программе и имеющий необходимый профессиональный опыт, может получить звание (международный сертификат) евроинженера.
Выпускники НИЯУ МИФИ востребованы в России и за рубежом. Они работают в ЦЕРНе, Брукхейвенской национальной лаборатории (BNL), Юлихском исследовательском центре (Forschungszentrum Jülich GmbH), Институте физики высоких энергий Китайской академии наук, Организации по исследованию ускорителей высоких энергий и более чем в 100 ведущих научных центрах по всему миру.
Milli Atom Araştırma Üniversitesi ‘MİFİ (МИФИ): fakülteler
НЭСПИ МИФИ создан для развития на его базе инновационного научно-образовательного центра мирового уровня в области наноэлектроники, спинтроники, фотоники, СВЧ-приборов, датчиков и генераторов терагерцовых сигналов.
Глобальные вызовы для электронной промышленности сегодня:
- Необходимость передачи и обработки больших объемов данных в режиме реального времени;
- Энергоэффективность компонентной базы;
- Увеличение степени интеграции в схемах и уменьшение активной площади транзистора.
Решения:
Использование передовых материалов в высокоскоростных компактных электронных устройствах;
Новая архитектура электронных компонентов;
Новые принципы в электронике – магнитные свойства материалов, квантовые компьютеры.
NESPI предлагает уникальные возможности стать профессионалом в области разработки и применения современной и перспективной электронной компонентной базы.
Выпускники обладают фундаментальными знаниями, владеют современными методами исследований, получают навыки изготовления и проектирования новых сложных устройств на стыке различных областей науки и техники.
Установки NESPI являются единственными в своем роде, предоставляющими передовые методы создания и изучения наноструктур и некремниевых электронных компонентов и схем, от основного материала до конечного устройства или функциональной системы.
Выпускники получают опыт практической работы с использованием передового научно-технического оборудования, хорошо разбираются в современной науке и технике, что делает их очень привлекательными на мировом рынке труда.
Работа над реальными исследовательскими проектами, изобретательскими задачами и созданием устройств уже на младших и старших курсах для бакалавров и особенно во время магистерской программы обеспечивает необходимую квалификацию, чтобы сделать карьеру в современной электронной промышленности.
Дополнительная информация —
http://nespi.
mephi.ru/index.php?lang=en.
(PDF) Кибернетические инфраструктуры количественных и качественных данных для распределенных городов
неформальная человеческая деятельность формирует процесс.Роль наблюдателя, который обрабатывает и контролирует систему,
, выбирая, фильтруя и делая выводы из своей личной субъективности. Как определяет второй закон термодинамики
, энтропия может увеличиваться с течением времени для изолированной системы, наблюдатель изолирует систему, лишая ее
формы взаимодействия и равновесия. Изолируя системы, отсутствие взаимосвязи между
официальной и неофициальной информацией обычного топографического анализа в городах способствует частичному пониманию нашей городской среды (Sassen, 2011) путем разделения социальных, экономических, физических
и испытывает геолокальные заказы.
Роль наблюдателя аналогична той, которую Джеймс Клерк Максвелл определил как своего демона (Максвелл, 1867 г.),
существо, способное действовать на молекулярном уровне, перемещать частицы и управлять глобальной системой
уменьшить энтропию, для этого он должен иметь знание и понимание локальных и глобальных масштабов
одновременно.
Первый позволяет ему точно знать, какую частицу он должен выбрать, а второй
дает ему контекст и информацию о том, где эта частица должна находиться в пространстве, наделяя его
определенным интеллектом, позволяя ему быть активным. элемент системы.
Непрерывный линейный поток информации от источника, расположенного в направлении из одной стороны в другую,
перерабатывающий входы в выходы это закрытая система, в которой контроллер играет важную роль, но не имеет
интеграции с самой системой. Регулирующая информация делает систему живой благодаря включению
обратной связи в качестве герменевтического и регенеративного процесса, нарушающего невзаимную линейность.
Модель жизнеспособной системы (VSM), разработанная британским кибернетиком Стаффордом Биром (1972 г.), представляет собой самовоспроизводящуюся
модель, способную рекурсивным образом учитывать изменения окружающей среды для непрерывной
адаптации во времени в причинно-следственной связи.
действие, учитывая действительность, возможность и потенциальность.Появление этой модели
дополнило то, как Норберт Винер определил кибернетику, включив
системы как часть среды, так что результат системы может информировать следующую итерацию и, таким образом,
далее, порождая рекурсию. В той же линии VSM кибернетика второго порядка интегрировала
наблюдателя в систему (фон Форестер, 1979), вовлекая людей и, следовательно, общество. По
позволяя наблюдателю проникнуть внутрь системы и выбирать свою собственную цель, давая ему автономию,
изменяя линейный образ мышления в западной культуре (Delanda, 2010),
Установлено как подходящее средство для снижения социальной энтропии кибернетика улучшает связь между
людьми, людьми и машинами и машинами с машинами (Wiener, 1958), позволяя открывать новые
формальные образы воображения, включая идею генеративных, рекурсивных и кибернетических систем в
измерениях искусства, государственное управление, архитектура и городской дизайн.
4. Гибридные кибернетические инфраструктуры.
В дизайнерской практике принято проектировать в контексте и пространстве, они придают масштаб и серьезность,
обеспечивая точность локальных взаимодействий в определенное время. Привязывая результат к определенному времени,
придают стабильность, замораживая любые шансы на дальнейший рост (Vivanco, 2016). Жизнь — это диссипативный
метастабильный процесс (Schenider, Sagan, 2008), где вещи находятся в непрерывном преобразовании посредством
обмена энергией, основанного на законах термодинамики.Остановка отдельных эволюционных
процессов от объектов влияет на большую экосистему, увеличивая энтропию.
Что не так нормально в практике проектирования, так это открытое проектирование путем включения этих эволюционных
принципов с учетом четвертого измерения (Fry, 2009), что означает расширение границ дизайна
и делает вещи открытыми и общедоступными, чтобы они могут находиться во владении людей (Delanda, 2010),
, фокусируя силу и потенциал объектов на расширении их раскрывающихся способностей (Domínguez
Rubio, 2015).
Для этого необходимо изменить представление о готовых объектах, понимаемых как продукты, на концепцию
прототипов, понимаемых как вмешательства. Чтобы добиться изменения, важно установить
разницу между прототипом и прототипированием.
Прототипы — это формальные представления проекций того, чем станет объект,
они передают расширенную идею, основанную на технологических, интерактивных и экономических аспектах. By
Улучшенный метод идентификации стохастической нелинейной системы с использованием авторегрессионной модели Гаммерштейна-Винера с ошибкой на выходе нечеткого типа, основанной на градиентном алгоритме, мультиинновации и методах фильтрации данных
В этой статье предлагается инновационный подход к идентификации нелинейных стохастических систем с использованием Модель Хаммерштейна-Винера (HW) с шумом авторегрессии ошибки вывода (OEA).Предлагаются две нечеткие системы для идентификации входных и выходных нелинейных блоков предлагаемой модели по заданным измерениям входных-выходных данных.
В данной работе необходимость в широко используемых допущениях, включающих известную структуру входных и/или выходных нелинейностей и/или обратимых нелинейных выходов, устраняется заменой промежуточных переменных и шума их оценками. Четыре алгоритма параметрической оценки для идентификации предложенной стохастической авторегрессионной модели HW с ошибкой вывода нечеткого типа (FSOEAHW) получены на основе алгоритма обратного распространения и мультиинновационных методов идентификации и фильтрации данных.Предлагаемые алгоритмы представляют собой улучшенный алгоритм градиента обратного распространения (IBPG), мультиинновационный алгоритм IBPG (MIIBPG), алгоритм фильтрации данных IBPG (FIBPG) и мультиинновационный алгоритм FIBPG (MIFIBPG). Исследуется сходимость алгоритмов оценивания параметров. Эффективность предложенных алгоритмов показана на приведенном имитационном примере.
1. Введение
Идентификация системы – это подход к моделированию динамической системы на основе данных наблюдений [1–9].
Он состоит в поиске подходящей математической модели, которая, насколько это возможно, аппроксимирует поведение системы, задавая соответствующую модель структуры и параметров, устанавливая связь между входными и выходными измерениями системы [10–13].
Все физические системы нелинейны, и для описания таких систем естественно использовать нелинейную модель. Поэтому в последнее время больше внимания уделяется нелинейным методам идентификации и управления, поскольку подходы, основанные на линейной идентификации и управлении, широко развиваются и становятся зрелыми.Одним из классов таких систем нелинейного моделирования являются так называемые блочно-ориентированные модели, которые могут быть представлены в различных конфигурациях, где каскадно соединены линейные динамические блоки и нелинейные статические или динамические подсистемы. Модель Хаммерштейна (H) (статический нелинейный блок, за которым следует динамический линейный блок) и система Винера (W) (линейная динамическая подсистема, за которой следует статический нелинейный блок) являются основным классом каскадных систем, которые широко используются во многих инженерные приложения в промышленной практике [14–22] и, следовательно, подходам к моделированию такого класса блочно-ориентированных моделей уделяется большое внимание в течение многих лет [23–36].
Системы Гаммерштейна и Винера объединяются вместе для создания более сложных подкатегорий, а именно модели Хаммерштейна-Винера (HW) (линейный блок каскадируется между двумя нелинейными подсистемами) и системы Винера-Гаммерштейна (WH) (нелинейный блок встроен между двумя линейные блоки). В частности, во многих случаях реальная система содержит нелинейности как исполнительного механизма, так и сенсора. Тогда уместно рассматривать входной нелинейный блок как нелинейность привода, а выходную нелинейную подсистему как датчик и/или нелинейность процесса.Модель HW имеет несколько преимуществ: (i) Она имеет физическое представление о нелинейных характеристиках реальной системы, что важно при анализе, мониторинге, диагностике и управлении системой. (ii) Динамика HW в основном создается линейной подсистемой. Затем можно было бы использовать разработанные линейные подходы. (iii) Когда выходная нелинейность имеет обратную функцию, методы линейного управления могут быть легко применены с желаемыми характеристиками.
Эта блочно-ориентированная форма модели прекрасно используется в различных областях, таких как электрические, механические, гидравлические и химические области [37–46].Следовательно, идентификация моделей HW стала активной темой исследований в настоящее время. В литературе предлагаются различные методы, которые можно условно разделить на разные категории: рекурсивные, итерационные, слепые, подпространственные, частотные, перепараметризация, методы декомпозиции и т.д. Основная идея вышеупомянутых методов состоит в том, что параметры модели аппроксимируются либо путем построения гибридной модели из нелинейной и линейной частей (например, перепараметризация, подпространство, декомпозиция и слепые методы [36, 43–46]), либо отдельными шагами, где оценки входных и выходных параметров нелинейных подсистем и динамической линейной части устанавливаются на основе шага оценивания неизмеряемых промежуточных переменных (таких как частотный, итерационный, рекурсивный, стохастический, корреляционный методы и специальный входной [35, 47– 51]).
Однако общее представление вышеупомянутых работ состоит в том, что шум процесса (т. е. шум между линейной динамической частью и нелинейным блоком) или выходные помехи (т. е. шум измерения, приведенный после нелинейного выходного блока) не учитывались, что не имеет место в практическом физическом процессе. Тогда более очевидно рассматривать некоторые стохастические возмущения. В связи с этим в литературе было предложено очень мало статей, посвященных стохастической модели HW.Например, в [43–49] авторы рассматривали конкретную структуру H-W, представляющую некоторые формы шума измерений. Для H-W с технологическим шумом некоторые работы были предложены в [49–53]. Эсмаилани и др. и Уиллс и др. [54–56] предложили методы идентификации класса систем H-W, представляющие шумы измерений и процессов.
Следует отметить, что применение вышеупомянутых подходов сильно ограничено из-за некоторых проблем. Фактически, соответствующие идеи ограничиваются полиномиальными формами входных и/или выходных нелинейных блоков или хорошо известными входными и/или выходными нелинейными характеристиками (такими как мертвая зона или люфт), но с неизвестными параметрами.
Следовательно, если нелинейность не является непрерывной или не имеет полиномиальной формы или с неизвестными характеристиками, алгоритмы не дают удовлетворительных результатов. Более того, проблема избыточности, приводящая к чрезмерному размеру матричных параметров HW, является еще одной лазейкой ранее упомянутых методов. Для компенсации этих недостатков искусственные интеллектуальные системы, такие как нейронные сети и нечеткие системы, могут быть исследованы для моделирования модели HW благодаря их свойству универсальной аппроксимации и их способности моделировать заданную нелинейную функцию с любой произвольной точностью.Учитывая, что структура HW должна быть обеспечена, проблема идентификации нейронной сети или HW нечеткого типа отличается (где требуется моделирование двух нелинейных блоков и динамической линейной части) от традиционной нейронной сети и нечеткой системы, которые фокусируется только на глобальном процессе нелинейного преобразования данных. В настоящее время сообщалось лишь о разрозненных работах по идентификации модели H-W на основе нейронных сетей и нечетких систем.
В [57, 58] предложен многоэтапный подход к созданию H-W модели рекуррентного типа нейронной сети, основанный на инициализации границы активной области, реализации собственной системы в частотной области и алгоритмах наименьших квадратов и рекурсивного рекуррентного обучения.H-W система нейро-нечеткого типа была представлена в [59] с использованием двухступенчатого входного сигнала. Для той же формы системы Jia et al. и Ли и др. [60, 61] объединили специальный входной сигнал и метод корреляции для раздельной и нерекурсивной идентификации параметров системы. Однако большинство из приведенных выше алгоритмов основаны на некоторых ограничительных условиях, особенно на предварительном знании некоторых параметров и предположении об обратимости выходной нелинейности для получения оценки промежуточной переменной, что не всегда так.Еще в [62] используется градиентный алгоритм обратного распространения для оценки совместно неизвестных параметров и промежуточных переменных системы H-W нейросетевого типа с полиномиальной формой входных и выходных нелинейных блоков.
Очевидно, что есть некоторые проблемы, которые необходимо решить при идентификации нелинейных процессов с использованием модели H-W для достижения удовлетворительных результатов. Первый заключается в том, как учитывать возмущения стохастического нелинейного процесса в описании модели H-W. Во-вторых, как идентифицировать модель H-W без каких-либо предварительных знаний о системе и с использованием только входных и выходных измерений.В-третьих, как приобрести мощную идентификационную способность модели H-W с минимальными привлекательными теоретическими предположениями. Последний заключается в определении алгоритма обучения, который можно использовать для достижения хорошей производительности.
Для решения вышеописанных проблем в этой статье представлен новый метод моделирования и идентификации параметров для идентификации нелинейного стохастического процесса, описываемого моделью H-W с авторегрессионной ошибкой на выходе нечеткого типа (FSOEAHW). Таким образом, по сравнению с существующими исследованиями, основные вклады этой статьи заключаются в следующем.
Первая оригинальность заключается в предложенной схеме H-W нечеткого типа. Фактически линейная часть рассматривается как дискретная передаточная функция, а авторегрессионная математическая модель выходной ошибки описывает возмущение процесса. Кроме того, две нечеткие модели предназначены для описания входных и выходных нелинейностей модели H-W только с знанием входных и выходных измерений. В результате предложенная модель может не только описать динамику такой нелинейной системы, работающей в стохастической среде, и избежать встречающихся входных и выходных ограничений нелинейных блоков, основанных на конкретных формах или формах базисных функций, но и исключить предположение об обратимости статической выходной части на основе на оценках внутренних переменных без проблемы завышения параметров модели.
Второе участие связано с предложенными алгоритмами оценки параметров. Основная идея состоит в том, чтобы объединить алгоритм градиента распространения с обратной связью с мультиинновационным методом и методом фильтрации данных для идентификации модели H-W нечеткого типа.
Предлагаемые алгоритмы идентификации основаны на измерении входных/выходных данных и аппроксимации всех внутренних переменных, полученных в результате предшествующих оценок соответствующих параметров. В этом случае предлагаются четыре алгоритма: алгоритм улучшенного градиента обратного распространения (IBPG), мультиинновационный алгоритм улучшенного градиента обратного распространения (MIIBPG) для повышения скорости сходимости с помощью мультиинновационного метода идентификации, алгоритм фильтрации данных IBPG (FIBPG). и мультиинновационный FIBPG (MIFIBPG).
Оставшаяся часть этого документа организована следующим образом. Рассматриваемая система описана в разделе 2. В разделе 3 разработаны алгоритмы оценивания параметров FSOEAHW, IBPG, MIIBPG, FIBPG и MIFIBPG, а также изучен анализ их сходимости. В разделе 4 представлены результаты моделирования. Некоторые выводы представлены в разделе 5.
2. Описание системы
2.1. Стохастическая авторегрессионная система Хаммерштейна-Винера с ошибками вывода (SOEAHW)
Рассмотрим стохастическую авторегрессионную систему Хаммерштейна-Винера с ошибками вывода (SOEAHW), представленную на рисунке 1.
В этой системе и являются входом и выходом системы соответственно. , , и являются внутренними переменными. Дискретная линейная передаточная функция окружена входным статическим нелинейным блоком и выходным статическим нелинейным блоком. Предполагается, что измеренный выходной сигнал содержит неизвестный компонент аддитивного шума, описываемый авторегрессионной математической моделью. представляет собой белый шум с нулевым средним значением и неизвестной дисперсией.
Первая неизмеряемая промежуточная переменная является выходом входного нелинейного блока и выражается следующим уравнением:
Линейная динамическая часть задается следующим выражением:
Вторая неизмеряемая промежуточная переменная может быть записана следующим образом:
Выход блока нелинейного вывода выражается следующим образом:
Шум определяется выражением
Имеем и .С учетом уравнений (4) и (5) выход системы выражается как
. наличие возмущения и большая сложность модели с минимумом привлекательных теоретических допущений, которые не всегда верны, особенно строгие ограничения, связанные с обратимостью нелинейного выходного блока и хорошо известными входными и/или выходными характеристиками нелинейных блоков (ii) Подходящая аппроксимация вышеописанная система, такая как сумма квадратов ошибок остаточного члена E (заданных следующим образом), которая должна быть уменьшена, насколько это возможно, с использованием адекватного алгоритма, где априори оценивается на выходе.
Для достижения вышеуказанных целей и на основе свойств универсальной аппроксимации нечетких систем мы предлагаем использовать две нечеткие модели для описания входной и выходной нелинейности.
2.2. Авторегрессионная модель Хаммерштейна-Винера со стохастической ошибкой вывода нечеткого типа (FSOEAHW)
Важнейшей задачей идентификации модели Хаммерштейна-Винера является эффективное моделирование двух статических нелинейных функций. Лучшее моделирование требует не только точной аппроксимации нелинейной функции, но и упрощения процесса идентификации.В литературе несколько исследований ограничиваются полиномиальной формой входных и/или выходных нелинейных блоков или известными входными и/или выходными нелинейными характеристиками (такими как мертвая зона или люфт), но с неизвестными параметрами [41–60, 63]. –74]. Следовательно, если нелинейность не является непрерывной или не имеет полиномиальной формы или с неизвестной характеристикой, алгоритмы не дают удовлетворительной работы.
Для компенсации вышеупомянутых недостатков, встречающихся в существующей структуре модели Гаммерштейна-Винера, в этой статье мы посвятили две нечеткие модели описанию входной и выходной нелинейностей модели H-W только со знанием входных и выходных измерений.
В этом разделе мы предлагаем разработать подход к моделированию нелинейного динамического процесса, протекающего в стохастической идентификации среды на основе нечеткой модели. Согласно предыдущему разделу, мы предлагаем новую стохастическую авторегрессионную HW-модель выходной ошибки (FSOEAHW) нечеткого типа, представленную на рисунке 2. Она состоит из двух статических нелинейных блоков, описываемых двумя независимыми нечеткими системами: динамический линейный блок и блок авторегрессионного шума. .
Тогда выход первой нечеткой системы можно сформулировать следующим образом: и представить, соответственно, соответствующий центр и ширину.является параметром вектора и является вектором входной информации.
Следует отметить, что функции принадлежности могут иметь несколько форм, таких как треугольная, трапециевидная и гауссова. Единственное условие, которое должно быть выполнено, это то, что он должен находиться в интервале [0, 1]. В литературе обычно используется форма Гаусса из-за ее простоты, гладкости и отсутствия нуля во всех точках. Она определяется всего двумя параметрами (центром и шириной) и является непрерывно дифференцируемой функцией [75–77].
Вторую неизмеримую промежуточную переменную ФСОЭАНВ можно записать так: где и – соответственно параметры вектора и вектор наблюдения линейной динамической части.
Выход второй нечеткой системы выражается где , где и являются центром и шириной m th функции принадлежности . и являются, соответственно, параметром вектора и вектором наблюдения выходного нелинейного блока. является нечетким правилом следствия m th и является соответствующим общим номером правила.
Шум выражается формулой (5).
Таким образом, выход системы можно переписать какили, что то же самое, записать в следующей матричной форме:
Следовательно, вектор параметров равен , а вектор наблюдения равен .
Обратите внимание, что все параметры вектора и векторы наблюдений (, , и ) неизвестны. Затем проблема состоит в разработке нового алгоритма идентификации, оценивающего неизвестные параметры и переменные с использованием входного измерения и выходного измерения и учитывающего цели, указанные в предыдущем абзаце.На основе оцененных параметров модели может быть построена математическая модель, идентифицирующая данную практическую стохастическую нелинейную динамическую систему.
3. Оценка параметров FSOEAHW
В этом разделе мы предлагаем использовать градиентный алгоритм обратного распространения для оценки неизвестных параметров и неизмеряемой переменной.
Градиентный алгоритм является важным инструментом в линейных и нелинейных задачах, в которых модификация оценок параметров достигается с помощью отрицательного направления градиента целевой функции.
На сегодняшний день и в области идентификации и управления предлагаются различные рекурсивные и итерационные градиентные алгоритмы [16, 17, 78–84]. Алгоритм стохастического градиента является базовым алгоритмом рекурсивной идентификации, который используется для изучения различных типов систем, таких как многомерные системы [85, 86] и нелинейные блочно-ориентированные системы [16, 17, 26, 87]. В [88] была представлена итерационная оценка параметра градиента для авторегрессионных систем с ошибкой на выходе с использованием иерархического принципа.Ю и др. [31] использовали алгоритм обратного распространения на основе градиента для идентификации системы типа нейронной сети Хаммерштейна. Равный алгоритм был расширен [62] для идентификации системы H-W типа нейронной сети.
Слабость градиентных методов заключается в том, что точность оценки недостаточна для целей контроля точности, а скорость сходимости очень низкая. Для устранения этих недостатков в литературе были предложены различные подходы.
Среди них мультиинновационный метод является одним из самых популярных методов, которые могут улучшить качество оценки параметров [89].Он состоит из оценки параметров, основанной не только на текущих данных, но и на предыдущих конечных данных на каждой итерации. В литературе представлены различные статьи для идентификации различных классов систем, таких как билинейные по параметру системы [90], многомерные линейные системы [91, 92], блочно-ориентированные системы [93–95] и т. д. .
Другим важным способом улучшения оценки параметров является использование мощного метода фильтрации данных. Основная идея, основанная на алгоритме идентификации, состоит в том, чтобы генерировать оценки параметров системы с использованием специального фильтра для фильтрации данных измерений, а затем идентифицировать отфильтрованную модель системы и отфильтрованную модель шума.В связи с этим структура системы идентификации будет изменена без устранения шума из данных или изменения взаимосвязи между переменными.
Этот метод показал свою эффективность при идентификации различных типов возмущенных систем, таких как рассмотренные в [70, 92, 96–104].
Далее мы представляем четыре алгоритма оценки, чтобы получить неизвестные параметры предлагаемой модели FSOEAHW. Первый алгоритм — это улучшенный градиент обратного распространения (IBPG), в котором используется алгоритм градиента на основе обратного распространения.Второй алгоритм, а именно MIIBPG, использует мультиинновационный метод и алгоритм IBPG для улучшения скорости сходимости посредством мультиинновационного метода идентификации. Наконец, с той же целью предлагаются алгоритм IBPG на основе фильтрации данных (FIBPG) и алгоритм FIBPG на основе мультиинноваций (MIFIBPG).
3.1. Алгоритм улучшенного градиента обратного распространения (IBPG)
Пусть , , и будут оцененными переменными, соответственно, промежуточных переменных , , и на шаге итерации t следующим образом: где оцененные параметры вектора на рекурсивном шаге t равны .
Предсказанные векторы наблюдения , , и с и в которых , , и , , , и оценки центра и ширины, соответственно, n th и m th параметров функций принадлежности и , и .
В результате априорная оценка выходного сигнала может быть выражена с помощью следующей эквивалентной регулируемой модели: где , , и где — оценка выходного шума, которая может быть выражена из уравнения (6) как .
Чтобы дать , заменяется его оценкой , что приводит к следующему выражению:
Используя уравнение (16), мы можем определить член ошибки оценки как
Используя градиентный алгоритм обратного распространения, каждый неизвестный параметр в модели FSOEHW обновляется в соответствии с формулой корректировки, полученной путем минимизации следующей функции квадратичной ошибки по отношению к этому параметру:
Путем рекурсивного применения цепного правила все неизмеряемые переменные должны быть сначала рассчитаны на основе значений параметра FSOEHW перед корректировкой (т..jpg)
е., параметры, полученные в результате предыдущего шага регулировки t-1 ). Затем каждый неизвестный параметр корректируется в соответствии со следующим выражением: где скорость обучения обновлений параметров. Параметры и – соответственно значения параметра после и до каждого шага настройки. представляет собой один из наборов параметров настройки FSOEAHW с .
Применяя алгоритм IBPG, уравнения настройки параметров первой нечеткой модели записываются следующим образом: где
Параметры линейной динамической части настраиваются в соответствии с уравнениями (28) и (29):
Наконец, уравнения настройки параметров вторая нечеткая система и аддитивный шум могут быть получены по следующим формулам: , (30) и (31), которые опущены в случае BPG.Фактически, наш алгоритм вдохновлен [15, 24]. Неизмеряемые переменные , , и пересчитываются на каждом рекурсивном шаге t на основе , , , , и , полученных в результате только что предыдущего рекурсивного шага, поскольку рассматриваемая система предполагается инвариантной, а линейная часть является динамической.
Затем рекомендуется рассмотреть вышеприведенные условия.
Ниже приводится сводка процедуры идентификации IBPG модели FSOEAHW: Шаг 1: случайным образом инициализируйте параметры FSOEAHW. Зафиксировать скорость обучения; .На каждой итерации t и для каждой выборки k повторите следующие шаги: Шаг 2: для входных данных вычислите, используя уравнение (13). Шаг 3: вычислить , , и соответственно на основе уравнений (14)–(16) и (18). Шаг 4: настроить параметры FSOEAHW с помощью уравнений (21)–(35). Шаг 5: рассчитать оценку шума по уравнению (17). Шаг 6: если критерии остановки E , заданные (7), и изменения параметров () меньше фиксированных малых значений, то остановитесь; в противном случае перейдите к шагу 2; .
3.1.1. Анализ сходимости алгоритма IBPG
Процедуры настройки параметров FSOEAHW основаны на выборе скорости обучения (). Слишком маленькое значение гарантирует сходимость, но с низкой скоростью обучения, тогда как слишком большое приводит к параметрическому расхождению.
В этом разделе теорема 1 дает подход к выбору удобного .
Теорема 1. Асимптотическая сходимость алгоритма IBPG гарантируется, если каждая скорость обучения каждого соответствующего регулируемого параметра выбрана так, чтобы удовлетворять где .
Доказательство. См. Приложение А.
3.2. Многоинновационный алгоритм улучшенного градиента обратного распространения ошибки (MIIBPG)
Мультиинновационный метод является эффективным инструментом для повышения скорости сходимости методов оценки. Вот почему он объединяется с различными алгоритмами оценивания, такими как градиентный алгоритм и метод наименьших квадратов в его рекурсивной и итерационной форме [33, 105–113]. В частности, хорошо известно, что алгоритм рекурсивного градиента имеет низкую скорость сходимости по сравнению с другими подходами к оценке [113].Этому недостатку способствуют многие факторы, в основном его зависимость только от текущих данных. По сути, на каждом шаге рекурсии градиентный алгоритм не использует предыдущие данные.
Он не имеет возможности использовать доступные данные на том же шаге.
Чтобы преодолеть эту проблему, в этом разделе мы предлагаем использовать многоинновационный алгоритм IBPG (MIIBPG), основанный на предыдущих конечных данных; то есть алгоритм MIIBPG использует текущие и предыдущие данные на каждой итерации t , что может повысить точность оценки параметра.
Элементарная идея состоит в том, чтобы расширить член ошибки, заданный (8) и обозначаемый скалярной инновацией, до инновационного вектора (называемого мультиинновацией) [109, 111, 113].
Определить вектор инноваций как где положительное целое число, обозначающее длину инновации, и l th скалярный член ошибки во времени, выраженный как
Этот метод предоставляет набор уравнений для обновления параметров, перечисленных ниже:где
Алгоритм идентификации MIIBPG может быть реализован на основе следующих шагов: Шаг 1: инициализировать параметры линейных динамических частей двух нечетких систем и выходного шума.
случайно.Зафиксируйте скорость обучения и длину инновации L ; . На каждой итерации t и для каждой выборки k повторите следующие шаги: Шаг 2: для , и для данного входа вычислите , , , , и используя уравнения (13)–(16) и (18) заменив к с кл . Шаг 3: настроить параметры FSOEAHW с помощью уравнений (40)–(53). Шаг 4: рассчитайте оценку шума по уравнению (17), заменив k на k-l . Шаг 5: если критерии остановки E , заданные (7), и изменения параметров () меньше фиксированных малых значений, то остановитесь; в противном случае перейдите к шагу 2; .
3.2.1. Анализ сходимости алгоритма MIIBPG
В этом разделе предполагается анализ сходимости алгоритма MIIBPG, который может применяться для оценки нелинейной стохастической системы, которую можно проиллюстрировать предложенной моделью FSOEAHW. Свойства сходимости алгоритма MIIBPG вводятся следующей теоремой.
Теорема 2. Асимптотическая сходимость алгоритма MIIBPG гарантируется, если скорость обучения соответствующего регулируемого параметра выбрана удовлетворяющей где .
Доказательство. См. Приложение B.
3.3. Алгоритм улучшенного градиента обратного распространения (FIBPG) на основе фильтрации данных
Метод фильтрации данных при идентификации системы используется для решения проблем оценки параметров систем, нарушаемых цветными шумами. В частности, элементарная идея состоит в том, чтобы использовать линейный фильтр для фильтрации данных ввода-вывода, чтобы исходные системы с цветными шумами преобразовывались в новые с белыми шумами. Затем структура системы преобразуется для упрощения без изменения соотношения между входами и выходами системы.Благодаря преимуществам метода фильтрации данных он широко применяется для идентификации различных систем и оценки параметров. Например, каждый из рекурсивных, итерационных и иерархических алгоритмов наименьших квадратов сочетается с методом фильтрации данных в задаче идентификации авторегрессионных линейных систем с ошибкой на выходе [114], управляемых линейных систем авторегрессии со скользящим средним с двумя входами и одним выходом [115].
], системы Хаммерштейна с конечной импульсной характеристикой со скользящим средним выходным шумом [116] и многопараметрическая бокс-подобная система Дженкинса [117].Точно так же градиентный алгоритм в его рекурсивной и итеративной форме используется с методом фильтрации данных для идентификации некоторых классов линейных и нелинейных систем, таких как линейная многопараметрическая авторегрессионная система скользящего среднего [101], линейная система в пространстве состояний в ее наблюдаемой канонической форме. возмущенный цветным шумом [118], и блочно-ориентированная система, такая как система с конечной импульсной характеристикой Хаммерштейна со скользящим средним выходным шумом [119].
Воодушевленные приведенным выше описанием, мы предлагаем в этом разделе объединить алгоритм IBPG (данный в Разделе 3.1) с методом фильтрации данных для повышения точности алгоритма IBPG. В нашем случае мы предлагаем ввести линейный фильтр для фильтрации данных измерений с целью оценки параметров и промежуточных переменных по двум критериям.
Определим, соответственно, отфильтрованную промежуточную переменную и отфильтрованный вывод как
У нас есть . Умножая обе части (11) на и используя (10), мы получаем
Таким образом, отфильтрованный вывод можно записать в матричной форме как
Таким образом, мы можем записать отфильтрованный вектор наблюдения следующим образом:
Следовательно, отфильтрованный вывод системы может быть определен как
Теперь цель состоит в том, чтобы разработать подход к оценке параметров FSOEAHW, основанный на градиентном алгоритме, с использованием измерения отфильтрованных данных и минимизацией отфильтрованной ошибки оценки, заданной выражением, где отфильтрованный оценочный вывод может быть выражен эквивалентным регулируемая модель: где будет выражено позже.Он представляет собой оцененный отфильтрованный вектор наблюдения, в котором оцениваемая промежуточная переменная определяется выражением (14).
Тем не менее, в уравнении (59) зависит от неизвестного параметра , . Чтобы нейтрализовать эту проблему, мы представляем двухшаговый алгоритм градиента. На первом этапе неизвестный параметр , , будет оцениваться путем минимизации критериев (заданных уравнением (62)). Впоследствии набор неизвестных параметров будет оцениваться с минимизацией критериев, заданных уравнением (66).
В действительности квадратичный критерий содержит неизмеряемый вектор выходного шума , поэтому оценка неизвестного параметра , , не может быть реализована.Тогда мы предлагаем заменить в (62) его оценку, заданную уравнением (64). После этого новые квадратичные целевые функции будут определены как где
Следовательно, уравнение оценивания параметра , , может быть получено с использованием градиентного алгоритма минимизации критериев следующим образом:
квадратичная целевая функция определяется следующим образом: где и выражаются, соответственно, где
У нас есть
Следовательно, остальные параметры настраиваются с использованием следующих уравнений с :где
Подводя итог алгоритму FIBPG, мы даем следующие шаги : Шаг 1: случайным образом инициализируйте параметры линейных динамических частей двух нечетких систем и параметры выходного шума.
Зафиксировать скорость обучения; . На каждой итерации t и для каждой выборки k повторить следующие шаги: Шаг 2: для ввода вычислить , , , и, используя, соответственно, уравнения (13)–(16), заменив k на kp . Шаг 3: расчет с использованием уравнения (64). Шаг 4: настроить параметр , , по уравнению (65). Шаг 5: вычислить , и на основе уравнений (66)–(68) соответственно. Шаг 6: обновить остальные параметры, используя уравнения (71)–(84). Шаг 7: если критерии остановки E , заданные (7), и изменения параметров () меньше фиксированных малых значений, то остановитесь; в противном случае перейдите к шагу 2; .
3.3.1. Анализ сходимости FIBPG
Этот подраздел посвящен анализу сходимости FIBPG, который может применяться для оценки параметров нелинейной системы, описываемой моделью FSEOFHW. Свойства сходимости алгоритма FIBPG определяются в следующей теореме.
Теорема 3. Асимптотическая сходимость FIBPG обеспечивается, если скорость обучения и другие параметры FSOEAHW удовлетворяют следующим условиям: где
— элемент множества параметров с .
Доказательство. См. Приложение C.
3.4. Алгоритм улучшенного градиента обратного распространения (MIFIBPG) на основе нескольких инноваций и фильтрации данных
Подобно разделу 3.2 и для повышения точности сходимости, мы можем объединить мультиинновационный подход с методом фильтрации данных, и тогда мы получим мультиинновационный алгоритм FIBPG (MIFIBPG). ) алгоритм.
Определить и следующим образом:где
Как и в предыдущем разделе и со ссылкой на алгоритм MIIBPG, первоначально параметр вектора корректируется для расчета ошибки инновационного вектора.Он обновляется по формуле (91) путем минимизации квадратичного критерия, заданного следующим уравнением:
Уравнения настройки всех остальных параметров получаются с использованием алгоритма MIFIBPG, минимизирующего функцию стоимости . Они перечислены следующим образом:гдегде
3.4.1. Исследование сходимости алгоритма MIFIBPG
Принимая во внимание упомянутые теоремы, мы можем легко продемонстрировать свойства сходимости этого алгоритма MIFIBPG для рассматриваемого FSOEAHW, что формулируется следующей теоремой.
Теорема 4. Сходимость алгоритма MIFIBPG обеспечивается, если скорости обучения и , где представляет каждый элемент множества параметров , при , удовлетворяют следующим неравенствам:где .
Доказательство теоремы аналогично приведенным в приложениях B и C для исследования сходимости алгоритмов MIIIBPG и FIBPG.
4. Пример
В этом разделе мы проведем иллюстративное моделирование, чтобы проверить производительность и эффективность разработанных алгоритмов.Поэтому мы рассматриваем нелинейную стохастическую систему, заданную математической моделью стохастической ошибки выхода Хаммерштейна-Винера, в которой ее блоки представлены следующими выражениями:
Набор из 9000 случайных значений от 0 до 4 используется в качестве входных данных представляет собой последовательность белого шума с нулевым средним значением и отношением шума к сигналу как . Вход и соответствующий выход представлены на рисунке 3.
Параметры, влияющие на предлагаемый FSOEAHW, выбираются следующим образом.
Входной нелинейный блок аппроксимируется с помощью нечеткой системы, состоящей из 8 правил, в которых последовательные части инициализируются случайным образом между 0 и 1 и параметрами функции принадлежности и инициализируются, соответственно, в интервалах и .
Начальные значения параметров , , , , и считаются соответственно как .
Выходная нелинейная часть изображается 6 нечеткими правилами, где параметры последующих частей инициализируются случайным образом между 0 и 1,5 и параметрами функции принадлежности и берутся, соответственно, в интервалах и . Численное моделирование реализовано для оценки параметров, влияющих на дискретное время FSOEAHW.
4.1. Параметрическая оценка с использованием алгоритма IBPG
Мы предлагаем оценивать параметры FSOEAHW с использованием алгоритма IBPG, описанного в разделе 3.1. Таким образом, мы демонстрируем результаты оценки, приводя кривые эволюции промежуточных переменных и оценок выхода , , , и на рисунке 4.
Кроме того, на рисунке 5 представлены кривые эволюции ошибки оценки и параметрического расстояния в котором и .
В табл. 1 представлены некоторые полученные численные значения оценок векторных параметров и соответствующая параметрическая ошибка для t = 0, 2000, 4000, 6000 и 9000. Кроме того, для оценки качества оценок в табл. ошибки оценивания (, , , , и ).
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||
0021Как отмечено в вышеупомянутых результатах моделирования, удовлетворительная оценка достигается с предлагаемым алгоритмом IBPG, несмотря на существование шум, воздействующий на выход процесса без ограничительных допущений. Кроме того, ошибки оценки параметров постепенно становятся меньше. Таким образом, оценки параметров ближе к истинным значениям, а нечеткие модели обеспечивают удовлетворительную точность оценки нелинейных входных и выходных блоков.
Для сравнения предлагаем привести результаты моделирования, в которых входная и выходная нелинейные части оцениваются двумя независимыми полиномиальными функциями, выражаемыми следующими уравнениями: где и — постоянные параметры. Тогда соответствующие системные параметры авторегрессионного HW (OEAHW) с выходной ошибкой равны , , , и .
Предлагаемый алгоритм IBPG используется для настройки параметров на основе обновленных уравнений, приведенных в Приложении D. Следует отметить, что OEAHW вдохновлен работой [24], где алгоритм IBPG используется для оценки полиномиальной модели Винера.
В этом смысле на рис. 6 показаны кривые эволюции оценок и параметрических ошибок для моделей OEAHW и FSOEAHW. В таблице 3 представлена оценка качества OEAHW.
| ||||||||||||||||||||||||||||||
Полученные результаты подтверждают, что модель FSOEAHW дает более удовлетворительную точность оценки по сравнению с моделью OEAHWM с полиномиальной формой. Благодаря способности нечетких систем обеспечивать хорошую аппроксимацию двух нелинейных частей, предложенный FSOEAHW достигает хороших результатов при сравнительно небольшом объеме вычислений, и полученная оценочная модель может правильно отражать динамику системы.
4.2. Параметрическая оценка с использованием алгоритма MIIBPG
Используя алгоритм MIIBPG для идентификации параметров FSOEAHW, оценки параметров векторов и соответствующие им параметрические ошибки приведены в таблице 4 для L = 2, 5 и 7. Кроме того, для тех же значений L , кривые эволюции и дисперсии ошибки оценки представлены, соответственно, на рисунках 7 и 8, где среднее статистическое значение ошибки оценки. Ошибки оценивания системных переменных приведены в табл. 5.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0125
2500
| ||||||||||||||||||||||||||||||||||||||||||||
4740 Изучив таблицы 4 и 5 и рисунки 7 и 8, мы можем подтвердить, что ошибки параметров и оценок постепенно уменьшаются с увеличением итерационной переменной и длины обновления.Кроме того, разработанный алгоритм MIIBPG обеспечивает более высокую производительность, чем стандартный алгоритм IBPG. Фактически оценки параметров системы сходятся к их истинным значениям, а ошибки оценивания уменьшаются до меньших значений. В этом направлении предлагаемый многоинновационный подход может эффективно оценивать параметры, а увеличение длины инновации может повысить точность оценки параметров и переменных и ускорить скорость сходимости, поскольку алгоритм использует больше информации на каждой итерации.
Следовательно, предложенный алгоритм эффективен для идентификации модели FSOEAHW.
4.3. Параметрическая оценка с использованием алгоритма FIBPG
В этом разделе эффективность алгоритма FIBPG по сравнению с алгоритмом IBPG хорошо видна путем визуализации кривых эволюции дисперсии ошибки оценки и параметрической ошибки, представленных соответственно на рисунках 9 и 10. фактически обеспечивается плавная и более точная параметрическая сходимость. Это более подтверждается изучением таблиц 6 и 7, которые показывают точность оценки модели FSOEAHW.
+
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2634
| |||||||||||||||||||||||||||||||
4.
4. Параметрическая оценка с использованием алгоритма MIFIBPGВ этой части мы используем алгоритм MIFIBPG для оценки параметров FSOEAHW. Таким образом, в таблицах 8 и 9 представлены оценки параметров и ошибки их оценки для L = 2, 5 и 7. Для одинаковых значений инновационной длины на рисунках 11 и 12 приведены дисперсия ошибки оценки и параметрическое расстояние .
предлагаемый мульти-инновационный подход в сочетании с данными фильтрации метод может эффективно и плавно оценить параметры и увеличивая длину инноваций дает хороший параметр точности оценки и ускоряет скорость сходимости, а затем устраняет недостатки градиентного алгоритма. 5. Заключение В данной статье рассматривается моделирование и идентификация систем SOEAHW на основе технологии искусственного интеллекта. Для идентификации входного и выходного нелинейных блоков используются две нечеткие модели с настраиваемыми параметрами. Выходная нелинейность может быть необратимой. ПриложениеA: Доказательство сходимости алгоритма IBPGРассмотрим функцию Ляпунова дискретного типа как [15, 51] Для простоты записи индекс t будет опущен.Изменение функции Ляпунова из-за процесса обучения, следовательно, разница ошибок может быть вычислена как Обозначим вектор параметров, подлежащий настройке на основе алгоритма IBPG и соответствующей ему скорости обучения, где Тогда можно вычислить как где обозначает изменение вектора параметров, сформулированное с помощью уравнений (20) и (П.3) как где Функция Ляпунова (П.1) является стационарной положительно определенной функцией. Таким образом, из (П.3)–(П.8) уравнение (П.2) будет выражаться в виде, где Теперь очевидно, что сходимость FOEAHW гарантирована, если . Тогда мы получаем условия теоремы 1. Это завершает доказательство. B: Доказательство сходимости алгоритма MIIBPGВ этом случае мы определяем функцию Ляпунова как выражено где Используя уравнения (Б.3)–(B.6), уравнение (B.2) переформулируется следующим образом: где Чтобы гарантировать, что достаточно иметь условия, описанные в теореме 2. сходимости, мы определяем кандидата Ляпунова V , который является положительно определенным и выражается в соответствии со следующим уравнением: где функция Ляпунова первого дискретного типа может быть определена как Изменение функции Ляпунова из-за процесса обучения отсюда Как и в приложении А, у нас есть следующее выражение:где Для того, чтобы уравнение (В.5) должно выполняться: где Вторая часть разности равна По тем же соображениям альтернирование функции Ляпунова выражается формулой где . Таким образом, за все время k , значит , где Следовательно, общая разница . Это подразумевает сходимость алгоритма FIBPG. На этом доказательство теоремы 3 завершено. эта учеба. Конфликт интересовАвторы заявляют об отсутствии конфликта интересов. Использование онтологий для улучшения поиска и навигации в электронной версии «Большой украинской энциклопедии» | РогушинаСемантическая МедиаВики. — https://www.semantic-mediawiki.org/wiki/Semantic_MediaWiki Гуарино Н. Формальная онтология в информационных системах. Формальная онтология в информационных системах. проц. ФОИС’98. 3-15. 1998. Ушольд М., Грюнингер М. Онтологии: принципы, методы и приложения. Обзор инженерных знаний. 1996. Том. 11, N 2. Ссылка .Асунсьон Г. Онтологическая инженерия: с примерами из областей управления знаниями, электронной коммерции и семантической сети (расширенная обработка информации и знаний). — http://www.amazon.com/gp/reader/1852335513/ref=sib_rdr_toc/. Рогушина Ю. Семантические ресурсы Wiki и их использование для построения персонализированных онтологий. Рогушина Ю.В. (2018) Теоретические средства использования онтологий для семантизации веб-ресурсов. Проблемы в программировании. № 2-3. С. 197-203. [на украинском] CrossRef Семантическая веб-активность W3C. -http://www.w3.org/2001/sw/Activity/. Рогушина Ю.В., Прийма С.М., Строкань О.В. (2017) Создание и использование ресурсов Semantic Wiki: учебник. Мелитополь, ФОП Одинорог Т.В. 169 с.[на украинском] Квиллиан М.Р. Семантическая память. В Мински, М. (ред.), Семантическая обработка информации. MIT Press, Кембридж, Массачусетс, 1968. .Коллинз, А., Лофтус, Э. Теория активации распространения семантической обработки. Психологический обзор. 1975. 82. С. 407-428. Перекрёстная ссылка Рада Р., Мили Х., Бикнел Э., Блеттнер М. Разработка и применение метрики в семантических сетях. IEEE Transaction on Systems, Man, and Cybernetics.1989. 19(1). С. 17-30. Перекрёстная ссылка Ричардсон Р. Ли Дж. Х., Ким М. Х., Ли Й. Дж. Поиск информации на основе концептуальной дистанции в иерархиях IS-A. Журнал документации. 1993. 49(2).С. 188-207. Перекрёстная ссылка Рада Р., Бикнелл Э. Ранжирование документов с тезаурусом. ЯСИС. 1989. 10(5). С. 304-310. Перекрёстная ссылка Ликок С., Ходоров М. WordNet: электронная лексическая база данных. Кембридж. 1998. С. 265. .Миллер Г. WordNet: интерактивная лексическая база данных. Международный журнал лексикографии, 3(4). (Специальный выпуск). 1990. Перекрёстная ссылка . Ву З., Палмер М. Семантика глаголов и лексический отбор.проц. 32-е ежегодное собрание Ассоциации вычислительной техники. Лингвистика. Лас-Крусес. 1994. Резник П. Семантическое сходство в таксономии: мера, основанная на информации, и ее применение к проблемам двусмысленности в естественном языке. Журнал исследований искусственного интеллекта. 1999. 11. С. 95-130. Перекрёстная ссылка Крюков К.В., Панкова К.В., Пронина В.А., Шипилина Л.Б. (2010) Меры семантической близости в онтологиях. Материалы МИФИ-2010, Том.5. Информационно-телекоммуникационные системы. Проблемы информационной безопасности. С. 75-78. [на русском] Тверской А. Признаки сходства. Психологический Rev. 1977. Vol. 84. С. 327. CrossRef .Бульсков Х., Кнаппе Р., Андреасен Т. Об измерении подобия для концептуальных запросов. проц. 5-й междунар. Конф. FQAS. LNCS. V. 2522. Берлин: Springer. 2002. С. 100. Ссылка .Левенштейн И.В. Двоичные коды, способные исправлять удаления, вставки и обращения.Кибернетика и теория управления. 1966. Том. 10. С. 707. Методические рекомендации по подготовке, редактированию и оформлению статей для Большой Украинской Энциклопедии (2015) / Под ред. Рогушина Ю.В. (2017) Использование онтологических знаний для семантического поиска сложных информационных объектов // Тр. ОСТИС-2017. С. 127-132. Рогушина Ю.В. (2017) Использование семантических свойств ресурсов Wiki для расширения функциональных возможностей «Большой украинской энциклопедии».Энциклопедии в современном информационном пространстве: коллективная монография / Под ред. Киридон А.М., Киев. С. 104-115. [на украинском] Гришанова И.Ю., Рогушина Ю.В. (2018) Адаптация технологических средств Semantic Mediawiki для нужд онлайн-версии Большой Украинской Энциклопедии // Энциклопедии в Украине: люди, идеи, шаги: коллективная монография / Под ред. Киридон А.М., Киев. С. 240-253. [на украинском] ПРОПОРЦИИ И НОРМЫ ХОЗЯЙСТВЕННОЙ ДЕЯТЕЛЬНОСТИ КАК ФАКТОР МАКСИМИЗАЦИИ ВАЛОВОЙ ДОБАВЛЕННОЙ СТОИМОСТИ В ПЕРЕХОДНОЙ ЭКОНОМИКЕ | ВЫКЛЮК Акбари, Р., Зиарати, К., 2011. Многоуровневый эволюционный алгоритм оптимизации числовых функций. Атенсия, М., Джойя, Г., Сандовал, Ф., 2005. Нейронные сети Хопфилда для параметрической идентификации динамических систем. Письма о нейронной обработке, 21, стр. 143-152. Балакришнан, С., Каннан, П.С., Аравиндан, К., Субатра, П., 2003. Выбросы в режиме онлайн и диспетчеризация экономической нагрузки с использованием адаптивной нейронной сети Хопфилда.Applied Soft Computing, 2(4), февраль, стр. 297-305. Коэн, М.А., Гроссберг, С.Г., 1983. Абсолютная стабильность формирования глобальных паттернов и параллельного хранения памяти конкурентными нейронными сетями». IEEE Transactions on Systems, Man and Cybernetics, 13(5), стр. 15-26. Дачин А., Бурча Ф.К., 2013 г. Структурные изменения и производительность в кризисный период в Румынии. Дело отрасли. Теоретическая и прикладная экономика, ХХ, 6(583), стр. 139-148. Гарг, Э.М., Сингх, Э.М., Гирдер, Э.В., 2012. Сравнительное исследование распределения экономической нагрузки (ELD) с использованием модифицированной нейронной сети Хопфилда. Гедзь М., 2014. Регулирование структурных изменений в экономике Украины. Российский академический журнал, 29(3), с.35-38. Хопфилд, Дж. Дж., 1982. Нейронные сети и физические системы с возникающими коллективными вычислительными способностями.Труды Национальной академии наук, 79, стр. 2554-2558. Katsikatsou, M., Moustaki, I., Yang-Wallentin, F., Jöreskog, K., 2012. Парная оценка правдоподобия для моделей факторного анализа с порядковыми данными. Вычислительная статистика и анализ данных, 56, стр. 4243-4258. Лабайе, Э., Шотил, П.Е., Богдан, В., Новак, Дж., Мишке, Дж., Фрук, М., Ионуциу, О., 2013. Новый рассвет: возобновление роста в Центральной и Восточной Европе, McKinsey Глобальный институт. Ли, К.Ю., Соде-Йоме А., Парк Дж. Х., 1998. Адаптивные нейронные сети Хопфилда для распределения экономической нагрузки. Максимов Ю.А., Филиповская Е.А., 1982. Алгоритмы решения задач нелинейного программирования, МИФИ, Москва, 52с. Мишра, С.К., Мишра, С.К., 2015. Сравнительное исследование решения проблемы экономичного распределения нагрузки в энергосистемах с экологической точки зрения. Procedia Computer Science, Международная конференция по компьютерам, коммуникациям и конвергенции (ICCC 2015), 48, стр.96-100 Мур, Дж. Х., Уэзерфорд, Л. Р., 2004. Моделирование решений в Microsoft Excel, 6-е изд., Издательство Вильямс, Москва, 1024 с. Pavelescu, F.M., 2012. Колебания экономической активности, отраслевое распределение валовой добавленной стоимости и величина обратного мультипликатора в Румынии за период 1989-2009 гг. Румынский журнал экономики, 35, 2(44), стр. 88-112. Пирог О.В., 2014. Структурные изменения в модели национальной экономики Украины под влиянием информатизации общества.Эффективная экономика, 7. Russu, C., 2015. Структурные изменения, произошедшие в обрабатывающей промышленности Румынии за последние два десятилетия. Procedia Economics and Finance, 2-я Международная конференция «Научные экономические исследования — теоретические, эмпирические и практические подходы», ESPERA 2014, 13-14 ноября 2014 г., Бухарест, Румыния Скрибане И., Екабсоне С., 2013. Структурные изменения в экономике Латвии после ее вступления в Европейский Союз.Интеллектуальная экономика, 7(1), стр. 29-41. Выклюк Ю.В., Ротарь А.В., Евдокименко В.В., 2013. Формирование стратегии воспроизводства моделей экономической деятельности в регионах на основе Soft Computing в условиях ускорения роста валового регионального продукта. Сборник научных статей. Экономические науки, 9, с. 99-116 Выклюк Ю.В., Евдокименко В.В., 2013. Развитие методов Soft Computing для оптимизации формирования стратегии воспроизводства моделей экономической деятельности в регионах. Выклюк Ю., Евдокименко В., 2014. Новые методы Soft Computing в формировании стратегии регионального развития. Журнал МЭСТ, 26(2), стр. 274-284. Wan-Liang, W., Xin-Li, X., Qi-Di, W., 2003. Подход нейронных сетей Хопфилда к задачам планирования рабочих мест, Интеллектуальное управление. В интеллектуальном управлении. 2003 Международный симпозиум IEEE по (стр.935-940). IEEE. Евдокименко В., 2013. Особенности управления воспроизводством социально-экономических процессов региона в современных условиях. Черновцы: Технодрук, 270 с. Чжан, Дж., Чанг, Х., Ло, В.Л., 2007. Вероятность адаптивного кроссовера и мутации на основе кластеризации для генетических алгоритмов. IEEE Transactions на Evolutionary. Вычисление, 11(3), стр. 326-335. конкурсных списков Обнинского института атомной энергии. Обнинское отделение нияу мифи (иате) (235). Отрывок, характеризующий Обнинский институт атомной энергии НИАУ Мифи1 / 5 ИАТЭ организует и проводит международные конференции по безопасности и подготовке кадров для атомной энергетики, по материаловедению и др. ИсторияОбнинский филиал МИФИ (1953-1985)Лаборатории «Б» МВД СССР — предприятию а/я 276 (далее) Министерства среднего машиностроения СССР требуются специалисты в области атомной энергетики.В 1950 году директор ФЭИ Д. И. Блохинцев подписал приказ об образовании на предприятии почтового ящика 276 заочных отделений Московского механического института (впоследствии преобразованного в филиал МИФИ) и МГУ. Организация этих отделов была возложена на заведующего лабораторией п/я 276 В. Н. Глазанова. В новом учебном заведении не было штатных преподавателей и учебной базы, но воспитательная работа велась удовлетворительно.В 1952 году учебное заведение преобразовано Министерством высшего и среднего специального образования СССР (приказ от 24 октября 1952 года) в вечернее отделение № 5 МИФИ. Проблема нехватки учебных помещений решена за счет части здания школы им. Шацкого и подвалов общежитий и помещений отдела кадров ФЭИ. Лабораторные работы проводились в соответствующих лабораториях ФЭИ с участием сотрудников этих лабораторий.Формально учебное заведение являлось филиалом МИФИ, фактически – филиалом ФЭИ. Для того, чтобы учебное заведение получило собственное здание, В.Н. Глазанов, будучи заместителем директора ФЭИ по науке, пошел на подлог, построив новое здание площадью 400 квадратных метров. м по документам на кафедру ФЭИ и передачу ее в 1959 году в филиал МИФИ. К началу 1960-х годов был сформирован коллектив преподавателей, учебно-вспомогательного персонала, созданы учебно-исследовательские лаборатории, мастерские, кабинеты, полностью оснащенные современным оборудованием и приборами.Лабораториями руководили первые сотрудники: Л.М. Мирошниченко, Т. В 1962 году на первый курс дневного отделения поступило 50 человек. В 1963 году был введен институт кураторов, работающих на общественных началах. Также на общественных началах начала работать воспитательная комиссия во главе со студентами, в обязанности которой входил контроль за успеваемостью студентов. Организация обучения включала УИР (учебно-научная работа) два дня в неделю, начиная с 4 курса, на базе ФЭИ, затем преддипломную практику и, наконец, диплом как завершающий этап два предыдущих вида обучения.Дипломы в результате были в основном высокого уровня. За двадцать лет существования филиала МИФИ количество штатных преподавателей выросло с трех в 1954 г. до ста четырех в 1974 г. Выпускники Обнинского филиала МИФИ уже в начале 1960-х гг. , а у профессорско-преподавательского состава возникла идея создания на базе филиала самостоятельного института для подготовки физиков в области биологии, радиологии, геологии и метеорологии. Команде преподавателей удалось убедить руководство Министерства среднего машиностроения не разбрасывать образовавшееся уникальное учебное заведение. В 1970 году филиал возглавил Г.А. Середы, при котором был построен учебный корпус, кафедры были частично оснащены современным оборудованием и приборами, новый институт получил хорошо подготовленные учебно-методические кадры. В 1985 году на базе филиала МИФИ был создан новый Институт атомной энергии (ИАТЭ), который возглавил Обнинский институт атомной энергии, организованный в 1985 году на базе филиала Московского инженерно-физического института, ныне — Обнинский институт атомной энергии — филиал Федерального государственного автономного образовательного учреждения высшего профессионального образования «Национальный исследовательский ядерный университет» МИФИ» — единственный специализированный вуз в России и СНГ, осуществляющий подготовку специалистов в области высоких технологий для предприятий и организаций атомной энергетики, науки и техники. В ИАТЭ обучается около 100 аспирантов, действуют 2 специализированных Совета по защите кандидатских диссертаций.Профессорско-преподавательский состав ИАТЭ принимает активное участие в научных исследованиях в области ядерной физики и ядерных реакций, физико-технических проблем атомной энергетики, надежности и безопасности объектов атомной энергетики и промышленности, построения математических моделей различных процессов и установок, компьютерные технологии, математика и информатика, исследования в области диагностики, физики металлов, теплофизики и др. Из Википедии, свободной энциклопедии
(ИАТЭ) – высшее учебное заведение в г. Обнинске, основанное в 1985 году на базе Обнинского филиала. До 2002 года он назывался Обнинский институт атомной энергии . В 2002 году он получил статус государственного технического университета и был переименован в Обнинский государственный технический университет атомной энергетики .29 апреля 2009 года приказом Федерального агентства по образованию № 491 Обнинский государственный технический университет атомной энергии реорганизован в форме присоединения к НИЯУ МИФИ с наименованием «Обнинский институт атомной энергии» — филиал федерального государственного бюджетного образовательного учреждение высшего профессионального образования «Национальный исследовательский ядерный университет «МИФИ». ИАТЭ – единственное высшее учебное заведение в России, осуществляющее подготовку специалистов в области высоких технологий для организаций атомной энергетики, науки и техники. Структура университета
Специальность
Научная деятельностьИАТЭ организует и проводит международные конференции по безопасности и подготовке кадров для атомной энергетики, по материаловедению и др. ИсторияОбнинский филиал МИФИ (1953-1985)Лаборатории «Б» МВД СССР — предприятию п/я 276 (далее) Министерства среднего машиностроения СССР требуются специалисты в области атомной энергетики.В 1950 году директор ФЭИ Д. И. Блохинцев подписал приказ об образовании на предприятии заочных кафедр Московского механического института (впоследствии преобразованного в филиал МИФИ) и МГУ. Организация этих отделов была возложена на заведующего лабораторией п/я 276 В.Н. Глазанов. В новом учебном заведении не было штатных преподавателей и учебной базы, но воспитательная работа велась удовлетворительно.В 1952 году учебное заведение преобразовано Министерством высшего и среднего специального образования СССР (приказ от 24 октября 1952 года) в вечернее отделение № 5 МИФИ. Проблема нехватки учебных помещений решена за счет части здания Шацкой школы и подвалов общежитий и помещений отдела кадров ФЭИ. Лабораторные работы проводились в соответствующих лабораториях ФЭИ с участием сотрудников этих лабораторий.Формально учебное заведение являлось филиалом МИФИ, фактически – филиалом ФЭИ. Для того, чтобы учебное заведение получило собственное здание, В.Н. Глазанов, будучи заместителем директора ФЭИ по науке, пошел на подлог, построив новое здание площадью 400 квадратных метров. м по документам на кафедру ФЭИ и передачу ее в 1959 году в филиал МИФИ. К началу 1960-х годов был сформирован коллектив преподавателей, учебно-вспомогательного персонала, созданы учебно-исследовательские лаборатории, мастерские, кабинеты, полностью оснащенные современным оборудованием и приборами.Лабораториями руководили первые сотрудники: Л.М. Мирошниченко, Т. В 1962 году на первый курс дневного отделения поступило 50 человек. В 1963 году был введен институт кураторов, работающих на общественных началах. Также на общественных началах начала работать воспитательная комиссия во главе со студентами, в обязанности которой входил контроль за успеваемостью студентов. Организация обучения включала УИР (учебно-научная работа) два дня в неделю, начиная с 4 курса, на базе ФЭИ, затем преддипломную практику и, наконец, диплом как завершающий этап два предыдущих вида обучения.Дипломы в результате были в основном высокого уровня. За двадцать лет существования филиала МИФИ количество штатных преподавателей выросло с трех в 1954 г. до ста четырех в 1974 г. Выпускники Обнинского филиала МИФИ уже в начале 1960-х гг. , а у профессорско-преподавательского состава возникла идея создания на базе филиала самостоятельного института для подготовки физиков в области биологии, радиологии, геологии и метеорологии. Команде преподавателей удалось убедить руководство Министерства среднего машиностроения не разбрасывать образовавшееся уникальное учебное заведение. директоров и ректоров
Известные учителяИзвестные выпускники и студентыБиблиография
Написать отзыв о статье «Обнинский институт атомной энергии Национальный исследовательский ядерный университет МИФИ»ПримечанияссылокОтрывок, характеризующий Обнинский институт атомной энергии Национальный исследовательский ядерный университет МИФИВ Николин день, в именины князя, вся Москва была у подъезда его дома, но он велел никого не принимать; но лишь некоторых, список которых он передал княжне Марье, велел позвать к обеду.Метивье, приехавший утром с поздравлениями, как врач, счел приличным de forcer la consigne [нарушить запрет], как он сказал княжне Марье, и вошел к князю. Случилось так, что в это утро дня рождения старый князь был в одном из своих худших настроений.  Он все утро ходил по дому, придираясь ко всем и делая вид, что он не понимает того, что ему говорят, и что его не понимают. Княжна Марья твердо знала это состояние тихой и озабоченной ворчливости, разрешавшееся обыкновенно взрывом ярости, и, как перед заряженным, взведенным ружьем, ходила все это утро, ожидая неизбежного выстрела.Утро перед приездом доктора прошло хорошо. Соскучившись по доктору, княжна Марья села с книгой в гостиной у двери, откуда ей было слышно все, что делалось в кабинете. Сначала она услышала голос одного Метивье, потом голос отца, потом оба голоса заговорили вместе, дверь распахнулась, и на пороге показалась испуганная красивая фигура Метивье с черным гребнем и фигура принца в шапке. и халат с изуродованным яростью лицом и опущенными зрачками глаз. — Вы не понимаете? — закричал князь, — но я понимаю! Французский шпион, Бонапарт-раб, шпион, вон из моего дома, — вон, говорю, — и он захлопнул дверь. Метивье, пожав плечами, подошел к мадемуазель Бурьен, прибежавшей на крик из соседней комнаты.  «Принц не совсем здоров», la bile et le transport au cerveau. Tranquillisez vous, je repasserai demain, [желчь и приливы к мозгу. Успокойся, я завтра приду,] — сказал Метивье и, приложив палец к губам, поспешно удалился. За дверью послышались шаги в ботинках и крики: «Шпионы, предатели, везде предатели! В твоем доме нет ни минуты покоя!» После отъезда Метивье старый князь позвал к себе дочь и вся сила его гнева обрушилась на нее. Это ее вина, что к нему допустили шпиона. .Ведь, сказал он, он велел ей составить список, а тех, кого нет в списке, не пускать. Зачем они отпустили эту сволочь! Она была причиной всего.С ней он не мог иметь ни минуты покоя, он не мог спокойно умереть, сказал он. — Нет, матушка, расходитесь, расходитесь, знаете ли, знаете ли! Я больше не могу, — сказал он и вышел из комнаты. И как бы боясь, что она не сможет как-то утешиться, вернулся к ней и, стараясь принять спокойный вид, добавил: — И не надо. Не думайте, что я сказал вам это в минуту сердечной, но я спокоен, и я обдумал это; и будет — расходитесь, ищите себе место!.  .. — Но он не выдержал. , и с тем гневом, который может быть только у человека любящего, он, видимо, страдая сам, потряс кулаками и крикнул ей: «А хоть бы какой-нибудь дурак женился на ней!» — Он хлопнул дверью, подозвал к себе m-lle Bourienne и замолчал в кабинете. В два часа избранные шесть человек собрались на ужин. Гости — знаменитый граф Ростопчин, князь Лопухин с племянником, генерал Чатров, старый, товарищ князя, и молодые Пьер и Борис Друбецкие — ждали его в гостиной. На днях Борис, приехавший в Москву на каникулы, пожелал быть представленным князю Николаю Андреевичу и сумел завоевать его благосклонность до такой степени, что князь сделал для него исключение из всех неженатых молодых людей, которых он не принимать. Княжеский дом был не то, что называется «светлым», а то был такой маленький кружок, который хотя и не был слышен в городе, но в котором было лестнее всего быть принятым. Борис понял это неделю назад, когда в его присутствии Ростопчин сказал главнокомандующему, позвавшему графа отобедать в Николин день, что его быть не может: — В этот день я всегда иду приложиться к мощам Князь Николай Андреевич.  — О да, да, — ответил главнокомандующий. — Что он?.. Маленькое общество, собравшееся в старинной, высокой, со старой мебелью, гостиной перед обедом, выглядело как торжественное заседание придворного совета. Все молчали, а если и говорили, то тихо. Князь Николай Андреевич вышел серьезный и молчаливый. Княжна Марья казалась еще более тихой и робкой, чем обычно. Гости неохотно обращались к ней, так как видели, что ей не до их разговоров. Один граф Ростопчин держал нить разговора, рассказывая о последних городских или политических новостях. В разговоре изредка принимали участие Лопухин и старый генерал. Князь Николай Андреевич слушал, как верховный судья слушал доносившийся ему доклад, лишь изредка заявляя молчанием или кратким словом, что он принял к сведению докладываемое ему. Тон разговора был таков, что было понятно, что никто не одобряет то, что делается в политическом мире. События были изложены, по-видимому, подтверждая, что дела шли все хуже и хуже; но в каждом рассказе и суде удивительно, как рассказчик останавливался или останавливался каждый раз на той границе, где суд мог относиться к лику Императора.  За обедом разговор зашел о последних политических известиях, о захвате Наполеоном владений герцога Ольденбургского и о враждебной Наполеону русской ноте, разосланной всем европейским дворам. — Бонапарт обращается с Европой, как с пиратом на завоеванном корабле, — сказал граф Ростопчин, повторяя уже несколько раз сказанную им фразу. — Вы только удивляетесь терпению или слепоте государей. Теперь дело доходит до папы, и Бонапарт уже не медлит свергнуть главу католической религии, и все молчат! Один наш государь протестовал против захвата владений герцога Ольденбургского.А потом… — Граф Ростопчин замолчал, чувствуя, что стоит на том месте, где осуждать уже нельзя. «Предложили вместо герцогства Ольденбургского другие владения, — сказал князь Николай Андреевич. — Как я крестьян с Лысых гор переселил в Богучарово и Рязань, так и он князей. — Le duc d»Oldenbourg supporte son malheur avec une force de caractere et une resignation admirable, [Герцог Ольденбургский переносит свое несчастье с недюжинной силой воли и покорностью судьбе, — сказал Борис, почтительно вступая в разговор.  Он сказал это потому, что проездом из Петербурга имел честь представиться герцогу. Князь Николай Андреевич посмотрел на молодого человека, как будто хотел сказать ему что-то об этом, но передумал, посчитав его слишком молодым для этого. № — Прочитал наш протест по делу Ольденбургских и удивился дурной формулировке этой записки, — сказал граф Ростопчин небрежным тоном человека, судящего хорошо знакомое ему дело. Пьер посмотрел на Растопчина с наивным удивлением, не понимая, почему его беспокоит скверная формулировка записки. – А не все ли равно, как написана записка, граф? — сказал он, — если его содержание сильное. — Mon cher, avec nos 500 mille hommes de troupes, il serait facile d’avoir un beau style, [Дорогой мой, с нашим 500-тысячным войском кажется легко выразиться в хорошем стиле] — сказал граф Ростопчин. Пьер понял отчего граф Ростопчин беспокоился о редакционной записке. — Кажется, писака совсем развелась, — сказал старый князь, — там в Петербурге все пишется, не только записки, но и новые законы пишутся.  Мой Андрюша написал там целый том законов для России. Все пишется! И он неестественно засмеялся. С минуту разговор был тихим; старый генерал обратил внимание с кашлем. — О последнем событии на смотре в Питере изволили узнать? как показал себя новый французский посланник! — Что? Да, я что-то слышал; он сказал что-то неловко перед Его Величеством. «Его величество обратил внимание на гренадерскую дивизию и на торжественный марш, — продолжал генерал, — и как будто посланник не обратил никакого внимания и как будто позволил себе сказать, что мы во Франции не обращаем внимания к таким мелочам.Государь ничего не соизволил сказать. При очередном смотре, говорят, государь так и не соизволил к нему обратиться. Все замолчали: нельзя судить об этом факте, который относился лично к государю. — Дерзайте! — сказал князь. Вы знаете Метивье? Я выгнал его сегодня. Он был здесь, меня впустили, как я ни просил никого не впускать, — сказал князь, сердито глядя на дочь. И он рассказал весь свой разговор с французским доктором и причины, по которым он был убежден, что Метивье — шпион.  Хотя эти причины были очень недостаточными и неясными, никто не возражал. К жаркому подавали шампанское. Гости встали с мест, поздравляя старого князя. Княжна Марья тоже подошла к нему. Он посмотрел на нее холодным, сердитым взглядом и подставил морщинистую, выбритую щеку. Все выражение его лица говорило ей, что он не забыл утреннего разговора, что решение его осталось в прежней силе и что только благодаря присутствию гостей он не сказал ей этого теперь. Когда они пошли в гостиную пить кофе, старики сели вместе. Князь Николай Андреевич оживился и высказал свое мнение о предстоящей войне. Он сказал, что наши войны с Бонапартом будут несчастны, пока мы будем искать союзов с немцами и вмешиваться в европейские дела, в которые нас втянул Тильзитский мир. Нам не нужно было воевать за Австрию или против Австрии. Наша политика вся на востоке, а по отношению к Бонапарту только одно — вооружение на границе и твердость в политике, и он никогда не посмеет перейти русскую границу, как на седьмом году.  — А куда нам, князь, с французами воевать! — сказал граф Ростопчин. — Можем ли мы поднять оружие против наших учителей и богов? Посмотрите на нашу молодежь, посмотрите на наших дам. Наши боги — французы, наше царство небесное — Париж. Он стал говорить громче, очевидно, чтобы все его слышали. «Французские костюмы, французские мысли, французские чувства!» Вы выгнали Метивье в шею, потому что он француз и негодяй, а наши барышни за ним ползают. Вчера был на вечере, так из пяти дам три католички и с разрешения папы в воскресенье шьют холст.А сами сидят почти голые, как вывески торговых бань, если можно так сказать. Эх, посмотри на нашу молодость, князь, взял бы из Кунсткамеры старую дубину Петра Великого, да по-русски борта отломил бы, всякая ерунда соскочила бы! Все замолчали. Старый князь посмотрел на Растопчина с улыбкой на лице и одобрительно покачал головой. — Ну, прощайте, ваше превосходительство, не болейте, — сказал Растопчин, вставая обычными своими быстрыми движениями и протягивая руку князю.  — Прощай, милый, — арфа, я всегда буду его слушать! — сказал старый князь, взяв его за руку и предлагая поцеловать в щеку. Другие поднялись с Ростопчиным. Княжна Марья, сидя в гостиной и прислушиваясь к этим разговорам и сплетням стариков, ничего не поняла из услышанного; она думала только о том, все ли гости заметили враждебное отношение отца к ней. Она даже не заметила того особого внимания и любезностей, которые Друбецкой, побывавший у них в доме в третий раз, оказывал ей в течение всего этого обеда. Все вузы Колумбийский университет Новиконтский морской колледж Хакасский технический институт им. Н.Ф.Катанова (филиал СФУ) Каспийский государственный технологический университет им. Есенова Актюбинский региональный государственный университет им. К. Жубанова Западно-Казахстанский государственный медицинский университет. М. Оспанова Алматинский университет управления Алматинский государственный колледж энергетики и электронных технологий Алматинский технологический университет Алматинский университет энергетики и связи Казахская академия транспорта и коммуникаций.М. Тынышпаева Казахская Головная Архитектурно-Строительная Академия Казахская Национальная Академия Искусств. 2019. Все права защищены. Карта сайта | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0058
1984
0005
Нечеткая модель, имеющая в качестве входных данных оценку линейного динамического выхода, аппроксимирует ее. Четыре заданных алгоритма оценки параметров (IBPG, MIIBPG, FIBPG и MIFIBPG) основаны на алгоритме рекурсивного градиента, многоинновационном методе и подходе к фильтрации данных.Они обладают свойством конвергенции и валидностью для онлайн-реализации. Результаты моделирования подтверждают эффективность предложенных алгоритмов. Однако недостатки предложенных алгоритмов заключаются, в частности, в обновленной инициализации параметров и выборе скорости обучения. На самом деле, хорошо известно, что уравнения настройки, основанные на градиентном алгоритме, напрямую зависят от выбора этих параметров, и они оказывают решающее влияние на сходимость и точность. Работа, представленная в этой статье, может быть распространена на другие классы стохастических нелинейных многомерных систем с цветным шумом.Кроме того, мы можем предложить адаптивное нечеткое управление нелинейным производственным процессом (например, практическим гидравлическим процессом) на основе представленной модели SOEAHW.
Наконец, можно предложить более подходящий подход к исследованию соответствующей скорости обучения и другим методам оптимизации, чтобы повысить производительность.
Материалы семинара CEUR 1631. 2016. С. 188-195.
, Смитон А.Ф., Мерфи Дж. Использование WordNet в качестве базы знаний для измерения семантического сходства между словами. Рабочий документ CA-1294, Дублинский городской университет, Школа компьютерных приложений, Дублин, 1994. ftp://ftp.compapp. dcu.ie/pub/w-papers/1994/CA1294.ps.Z
С. 133-138. Перекрёстная ссылка
Киридон А.М., Киев, Киев, 120 с. [на украинском]
Международный журнал промышленных инженерных вычислений, 2, стр. 419-430.
International Journal of Computing & Business Research, Proceedings of I-Society 2012, доступно по адресу: http://www.researchmanuscripts.com/isociety2012/43.pdf
IEEE Transactions on Power Systems, 13(2), май, стр. 519-526.
Режим доступа: http://www.economy.nayka.com.ua/?op=1&z=3170
Материалы Международной научной конференции «Информационные технологии, экономика и право». Состояние и тенденции развития, Черновцы.
Этот заказ был запущен почти через два года, в августе 1954 года, без штатного расписания и финансирования.
Е. Прокурат, М.В. Борисов, Г.М. Назарова, Ю.В. А. Федоров.
Учебные планы, разработанные институтом, были согласованы с соответствующими министерствами. В 1963 году появился приказ Министерства высшего и среднего образования СССР об организации на базе филиала самостоятельного института с приемом 275 человек при финансировании Министерства среднего машиностроения СССР для строительство учебного корпуса и общежития для студентов. Был разработан проект учебного корпуса, строительство которого было завершено в 1964 году до 1 этажа.Однако в том же году, после смерти шестидесятишестилетнего В.Н. Глазанов, генеральный подрядчик ФЭИ, передал здание Центральному институту повышения квалификации (ЦИПК). Само существование отделения было поставлено под сомнение. В 1966 году вышел приказ министра высшего образования СССР В.П. Елютин и министр среднего машиностроения СССР Е.П. Славского закрыть очное отделение в связи с нецелесообразностью параллелизма в подготовке физиков в Обнинском филиале и самом МИФИ.
Три года (1968, 1969, 1970) институт существовал полулегально. Был дневной отдел, который согласно приказу был ликвидирован. В 1969-1970 годах профессорско-преподавательский состав при поддержке всех научных институтов Обнинска добивался открытия филиала. В 1970 году вышел приказ об открытии в Обнинске филиала МИФИ для подготовки специалистов по автоматизированным системам управления (АСУ) и вычислительной технике.
ИАТЭ имеет лицензию Министерства образования Российской Федерации на право ведения образовательной деятельности в сфере среднего, высшего, послевузовского и дополнительного образования. 
ИАТЭ организует и проводит международные конференции по безопасности и подготовке кадров для атомной энергетики, по материаловедению и др.
Обнинск, Калужская область
Бакалавр техники и технологий.
Инженер.
Психолог, преподаватель психологии.
Этот заказ был запущен почти через два года, в августе 1954 года, без штатного расписания и финансирования.
Е. Прокурат, М.В. Борисов, Г.М. Назарова, Ю.В. А. Федоров.
Учебные планы, разработанные институтом, были согласованы с соответствующими министерствами. В 1963 году появился приказ Министерства высшего и среднего образования СССР об организации на базе филиала самостоятельного института с приемом 275 человек при финансировании Министерства среднего машиностроения СССР для строительство учебного корпуса и общежития для студентов. Был разработан проект учебного корпуса, строительство которого было завершено в 1964 году до 1 этажа.Однако в том же году, после смерти шестидесятишестилетнего В.Н. Глазанов, генеральный подрядчик ФЭИ, передал здание Центральному институту повышения квалификации (ЦИПК). Само существование отделения было поставлено под сомнение. В 1966 году вышел приказ министра высшего образования СССР В.П. Елютин и министр среднего машиностроения СССР Е.П. Славского закрыть очное отделение в связи с нецелесообразностью параллелизма в подготовке физиков в Обнинском филиале и самом МИФИ.
Три года (1968, 1969, 1970) институт существовал полулегально. Был дневной отдел, который согласно приказу был ликвидирован. В 1969-1970 годах профессорско-преподавательский состав при поддержке всех научных учреждений Обнинска добивался открытия филиала. В 1970 году вышел приказ об открытии в Обнинске филиала МИФИ для подготовки специалистов по автоматизированным системам управления (АСУ) и вычислительной технике.
— 2003. — № 4 (87), ноябрь.
E il est tres melancolique aupres de m lle Karagin [надо быть меланхоликом. И он очень меланхоличен с m elle Карагиной,] — сказал Пьер. .jpg)
Не слушай меня, забудь, что я тебе говорил. 
Т. Жургенова Казахский национальный аграрный университет Казахский национальный медицинский университет им. С.Д. Асфендиярова Казахский национальный педагогический университет им. Казахский национальный технический университет имени Абая Аль-Фараби Казахский национальный университет имени К. И. Сатпаева им. Казахский университет имени аль-Фараби международные отношения и мировые языки. Абылай хана Казахстанский институт управления, экономики и прогнозирования Казахстанско-Британский Технический Университет Казахстанско-Немецкий Университет Казахстанско-Российский Медицинский Университет Международный Университет Информационных Технологий Новый Экономический Университет им.Т. Рыскулова Университет международного бизнеса Университет Туран Донбасский государственный технический университет Альметьевский государственный нефтяной институт Арзамасский государственный педагогический институт им. А. П. Гайдара Арзамасский политехнический институт (филиал НГТУ) Армавирская государственная педагогическая академия Армавирский лингвистический университет Северный (Арктический) федеральный университет им.
М.В. Ломоносова Северный государственный медицинский университет Северный институт предпринимательства Евразийского национального университета им. Л.Н. Гумилева Казахский агротехнический университет.С. Сейфуллина Казахский гуманитарно-юридический университет Казахский университет технологии и бизнеса Медицинский университет Астана Астраханский государственный архитектурно-строительный университет Астраханский государственный медицинский университет Астраханский государственный технический университет Ачинский колледж промышленных технологий и бизнеса Азербайджанский медицинский университет Балаковский технологический институт и управления Барановичский государственный университет Алтайская академия экономики и права Алтайская государственная академия культуры и искусств Алтайский государственный аграрный университет Алтайский государственный медицинский университет Алтайский государственный педагогический университет Алтайский государственный технический университет им.И.И. Ползунова Алтайский государственный университет Алтайский филиал РАНХиГС (СибАГС АФ) Алтайский институт экономики и права Колледж 103 Белоцерковский национальный аграрный университет Белгородская государственная сельскохозяйственная академия.
В.Я. Горина Белгородский государственный институт искусств и культуры Белгородский государственный национальный исследовательский университет Белгородский государственный технологический университет им. В.Г. Шухова Белгородский университет кооперации, экономики и права Белгородский юридический институт МВД России Бердянский государственный педагогический университет им.Осипенко Бердянский университет управления и бизнеса Бийский технологический институт (филиал АГТУ им. Ползунова) Кыргызская государственная медицинская академия им. И.К. Ахунбаева Кыргызский государственный университет имени И. Арабаева Кыргызский государственный университет строительства, транспорта и архитектуры Кыргызский национальный университет им. ж. Баласагына Кыргызско-Российская академия образования Кыргызско-Российский Славянский Университет. Ельцина Амурская государственная медицинская академия Амурский государственный университет Дальневосточный государственный аграрный университет Бокситогорский институт (филиал Ленинградского государственного университета имени А.
С. Пушкина) Братский государственный университет Брестский государственный технический университет Брестский государственный университет имени А.С. В ВИДЕ. Пушкина Брянская государственная инженерно-технологическая академия Брянский государственный аграрный университет Брянский государственный технический университет Брянский государственный университет им. академик И.Г. Петровского Брянский институт управления и бизнеса Брянский филиал РАНХиГС (ОРАГС БФ) Бухарский инженерно-технологический институт Великолукская государственная академия физической культуры и спорта Великолукская государственная сельскохозяйственная академия Винницкий государственный педагогический университет им.М. Коцюбинского Винницкий национальный аграрный университет Винницкий национальный медицинский университет им. Н.И. Пирогова Винницкий национальный технический университет Винницкий торгово-экономический институт (филиал КНТЭУ) Винницкий финансово-экономический университет Витебская государственная академия ветеринарной медицины Витебский государственный медицинский университет Витебский государственный технологический университет Витебский государственный университет им.
П. М. Машерова Владивостокский государственный университет экономики и сервиса Дальневосточный государственный технический рыбохозяйственный университет Дальневосточный государственный технический университет Дальневосточный федеральный университет Морской государственный университет им.адмирал Г.И. Невельского Тихоокеанский государственный медицинский университет Горский государственный аграрный университет Северо-Кавказский горно-металлургический технологический университет (СКГМИ) Северо-Осетинская государственная медицинская академия Северо-Осетинский государственный университет им. К. Хетагуров Владимирский государственный университет Столетовы Владимирский филиал РАНХиГС (РАГС ВФ) Волгоградская государственная академия физической культуры Волгоградский государственный аграрный университет Волгоградский государственный архитектурно-строительный университет Волгоградский государственный институт искусств и культуры Волгоградский государственный медицинский университет Волгоградский государственный социально-педагогический Университет Волгоградский государственный технический университет Волгоградский государственный университет Волгоградский институт бизнеса Волгоградский филиал РАНХиГС (ВАГС) Волгодонский инженерно-технический институт Национального исследовательского ядерного университета МИФИ Волжский политехнический институт (филиал ВолгГТУ) Волковысский педагогический колледж им.
Купара ГрГУ Вологодская государственная молочная академия. Н. В. Верещагина Вологодский государственный университет Вологодский институт права и экономики ФСИН России Педагогический институт ВГУ Воронежская государственная лесотехническая академия Воронежская государственная медицинская академия. Н.Н. Бурденко Воронежский государственный аграрный университет. Императора Петра I Воронежский государственный архитектурно-строительный университет Воронежский государственный институт физической культуры Воронежский государственный медицинский университет им.ГОСТИНИЦА. Бурденко Воронежский государственный педагогический университет Воронежский государственный технический университет Воронежский государственный университет Воронежский государственный университет инженерных технологий Воронежский институт высоких технологий Воронежский институт МВД России Воронежский институт экономики и права Институт управления, маркетинга и финансов Международный институт Компьютерные технологии Государственный институт экономики, финансов, права и технологий Глазовский государственный педагогический институт.
В.Г. Короленко Глуховский национальный педагогический университет им. А. Довженко Белорусский государственный университет транспорта Белорусский торгово-экономический университет потребительской кооперации Гомельский государственный аграрно-экономический колледж Гомельский государственный медицинский университет Гомельский государственный технический университет им. НА. Сухого Гомельский государственный университет им. Франциска Скорины Белорусская государственная сельскохозяйственная академия Горловский государственный педагогический институт иностранных языков ДГПУ Горно-Алтайский государственный университет Гродненский государственный аграрный университет Гродненский государственный медицинский университет Гродненский государственный университет им.Я. Купала Чеченский государственный университет Днепропетровская государственная финансовая академия Днепропетровская медицинская академия МЗ Украины Днепропетровский государственный аграрно-экономический университет Днепропетровский государственный университет внутренних дел Днепропетровский национальный университет железнодорожного транспорта им.
Академика В. Лазаряна Днепропетровский национальный университет им. Олеся Гончара Днепропетровский университет им. А. Нобеля Национальная металлургическая академия Украины Национальный горный университет Приднепровская государственная академия строительства и архитектуры Украинский государственный химико-технологический университет Московский государственный физико-технический университет (МФТИ) Академия гражданской защиты МЧС ДНР Донбасская юридическая академия Донецкий институт железнодорожного транспорта Донецкий национальный медицинский университет.М. Горького Донецкий национальный университет Донецкий национальный университет экономики и торговли. М. Туган-Барановского Донецкий колледж промышленной автоматизации Донецкий юридический институт МВД Украины Дрогобычский государственный педагогический университет им. И. Франко Авиценна Таджикский государственный медицинский университет Абуали ибн Сино (Авиценна) Таджикский государственный педагогический университет имени Садриддина Айни Таджикский технический университет им.
М. Осими Евпаторийский институт общественных наук (филиал КФУ) Екатеринбургский государственный театральный институт Институт международных отношений Колледж железнодорожного транспорта Российский государственный профессионально-педагогический университет Уральская государственная архитектурно-художественная академия Уральская государственная консерватория.член парламента Мусоргского Уральский государственный аграрный университет Уральский государственный горный университет Уральский государственный лесотехнический университет Уральский государственный медицинский университет Уральский государственный педагогический университет Уральский государственный университет путей сообщения Уральский государственный экономический университет Уральский государственный юридический университет Уральский институт бизнеса. И.А. Ильина Уральский институт государственной противопожарной службы МЧС России Уральский институт коммерции и права Уральский институт РАНХиГС (УрАГС) Уральский институт экономики, управления и права Уральский техникум автомобильного транспорта и сервиса Уральский технический институт связи и информатики (филиал СибГУТИ) Уральский федеральный университет им.
Б.Н. Ельцина «УПИ» Уральский финансово-правовой институт Елабужский институт Казанского (Приволжского) федерального университета (бывший ЕГПУ) Елецкий государственный университет им. Я. Бунина Ереванский государственный университет Житомирский государственный технологический университет Житомирский государственный университет им. Ивана Франко Житомирский институт сестринского дела Житомирский национальный агроэкологический университет Заволжский автомобильный колледж Запорожская государственная инженерная академия Запорожский государственный медицинский университет Запорожский институт экономики и информационных технологий Запорожский национальный технический университет Запорожский национальный университет Институт искусств и информационных технологий Московский филиал Ивано-Франковский национальный медицинский университет Ивано-Франковский национальный технический университет нефти и газа В.Стефаника Ивановская государственная архитектурно-строительная академия Ивановская государственная медицинская академия Ивановская государственная сельскохозяйственная академия Ивановский государственный университет Ивановский государственный химико-технологический университет Ивановский государственный энергетический университет им.
В И. Ленина Текстильный институт ИвГПУ Московский областной институт управления и права Ижевская государственная медицинская академия Ижевская государственная сельскохозяйственная академия Ижевский государственный технический университет им. М. Т. Калашникова Камский институт гуманитарных и инженерных технологий Удмуртский государственный университет Удмуртский республиканский социально-педагогический колледж Измаильский техникум механизации и электроэнергетики сельского хозяйства Байкальский государственный университет Иркутский государственный аграрный университет им.А.А. Ежевского Иркутский государственный лингвистический университет Иркутский государственный медицинский университет Иркутский государственный университет Иркутский государственный университет путей сообщения Иркутский национальный исследовательский технический университет Педагогический институт (филиал ИГУ) Сибирская академия права, экономики и управления Юридический институт (филиал ИГУ) Национальный университет государственной налоговой службы Служба Украины Марийский государственный университет Межрегиональный открытый социальный институт Межрегиональный центр «Непрерывное профессиональное образование» Поволжский государственный технологический университет Академия социального образования Институт социально-гуманитарных знаний Институт экономики и финансов КФУ Институт экономики, управления и права Казанская государственная академия ветеринарной медицины .
Н.Э. Баумана Казанская государственная консерватория (академия) Н.Г. Жиганова Казанский государственный аграрный университет Казанский государственный архитектурно-строительный университет Казанский государственный медицинский университет Казанский государственный университет культуры и искусств Казанский государственный энергетический университет Казанский кооперативный институт (филиал РУК) Казанский национальный исследовательский Технический университет. А. Н. Туполева Казанский национальный исследовательский технологический университет Казанский федеральный университет Приволжская государственная академия физической культуры, спорта и туризма Татарский государственный гуманитарно-педагогический университет Университет управления ТИСБИ Калачеевский аграрный колледж Балтийская государственная академия рыбного флота Балтийский информационный колледж Балтийский федеральный университет им.И. Канта Калининградский государственный технический университет Санкт-Петербургский университет сервиса и экономики (Калининградский филиал) Калужский государственный университет им.
К. Э. Циолковского Калужский филиал РАНХиГС Каменец-Подольский национальный университет. И. Огиенко Подольский государственный аграрно-технический университет Камышинский технологический институт (филиал ВолгГТУ) Карагандинский государственный медицинский университет Карагандинский государственный технический университет Карагандинский государственный университет им. Е.А. Букетова Карагандинский университет Болашак Карагандинский экономический университет имени Сулеймана Демиреля Кемеровский государственный медицинский университет (бывший КемГМА) Кемеровский государственный сельскохозяйственный институт Кемеровский государственный университет Кемеровский государственный университет культуры и искусств Кемеровский технологический институт пищевой промышленности Кузбасский государственный технический университет Кузбасский институт экономики и права Керчь Государственный морской технологический университет Государственный университет телекоммуникаций Государственный экономико-технологический университет транспорта Европейский университет финансов, информационных систем, управления и бизнеса Киевская государственная академия водного транспорта им.
Конашевича-Сагайдачного Киевский медицинский университет УАНМ Киевский национальный лингвистический университет Киевский национальный торгово-экономический университет Киевский национальный университет им. Т. Шевченко Киевский национальный университет культуры и искусств Киевский национальный университет строительства и архитектуры Киевский национальный университет театра, кино и телевидения им. И.К. Карпенко-Карого Киевский национальный университет технологий и дизайна Киевский национальный экономический университет. В. Гетьмана Киевский славянский университет Киевский университет. Б.Гринченко Киевский юридический университет Национальной академии наук Украины Киевский университет туризма, экономики и права Международный научно-технический университет. Ю. Бугая Межрегиональная академия управления персоналом Национальная академия внутренних дел Украины Национальная академия руководящих кадров культуры и искусств Национальная академия статистики, учета и аудита Национальная академия управления Национальная музыкальная академия Украины.
Национальный авиационный университет им. П. И. Чайковского Национальный медицинский университет им.А.А. Богомольца, Национальный педагогический университет им. член парламента Драгоманова Национальный технический университет Украины «Киевский политехнический институт» Национальный транспортный университет Национальный университет «Киево-Могилянская академия» Национальный университет биоресурсов и природопользования Национальный университет пищевых технологий Национальный университет физической культуры и спорта Украины Открытый международный университет развития человека Украина Украинский государственный университет финансов и международной торговли Самарская государственная сельскохозяйственная академия Волго-Вятский институт (филиал МГЮА) Вятская государственная сельскохозяйственная академия Вятский государственный гуманитарный университет Вятский государственный университет Вятский социально-экономический институт Московский финансово-юридический университет Кировский филиал Кировоградский Летная академия Национального авиационного университета Кировоградский государственный педагогический университет им.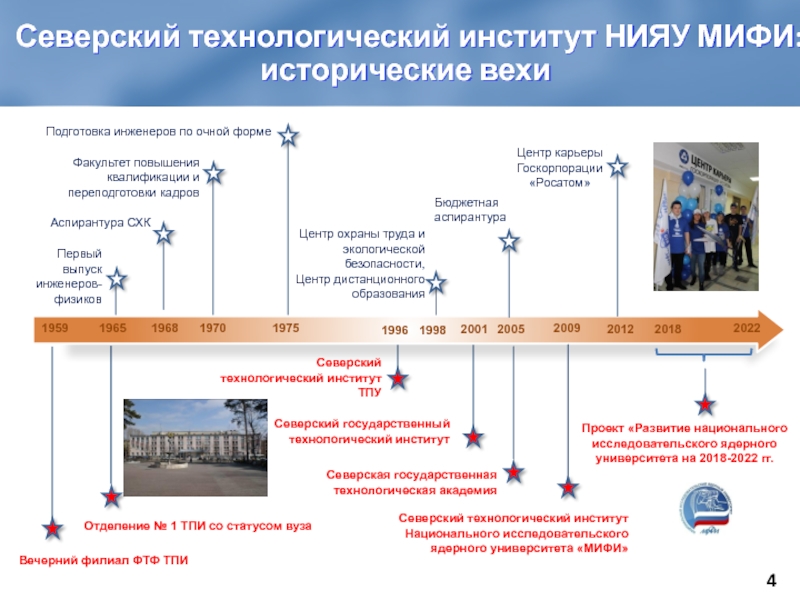
Винниченко Кировоградский институт регионального управления и экономики Кировоградский национальный технический университет Государственный аграрный университет Молдовы Государственный университет медицины и фармакологии. Николае Тестемицану Международный Независимый Университет Молдовы Ковровская Государственная Технологическая Академия. В.А. Дегтярева Коломенский институт-филиал Московского государственного медицинского университета Московский государственный областной социально-гуманитарный институт Амурский гуманитарно-педагогический государственный университет Комсомольский-на-Амуре государственный технический университет Конотопский институт СумГУ Финансово-технологическая академия Костанайский государственный университет им.Ахмет Байтурсынов Костромской государственный технологический университет Костромской государственный университет им. НА. Некрасова Донбасская государственная инженерная академия Донбасская национальная академия строительства и архитектуры Донецкий национальный технический университет Красноармейский индустриальный институт ДонНТУ Краснодарский государственный университет культуры и искусств Кубанский государственный аграрный университет Кубанский государственный медицинский университет Кубанский государственный технологический университет Кубанский государственный университет Кубанский государственный университет физической культуры, Спорт и туризм Кубанский социально-экономический институт Современная академия гуманитарных наук Гуманитарный институт СФУ Инженерно-строительный институт СФУ Институт архитектуры и дизайна СФУ Институт горного дела, геологии и геотехнологии СФУ Естественно-гуманитарный институт СФУ Институт технической физики и радиоэлектроники СФУ Институт космических и информационных технологий СФУ Институт нефти и газа СФУ Институт педагогики, психологии и социологии СФУ Институт управления бизнес-процессами и экономики СФУ Институт филологии d Языковое общение СФУ Институт фундаментальной биологии и биотехнологии СФУ Институт цветных металлов и материаловедения СФУ Институт экономики, менеджмента и природопользования СФУ Красноярская государственная академия музыки и театра Красноярская государственная архитектурно-строительная академия СибФУ Красноярский государственный аграрный университет Красноярский государственный Медицинский университет.
В.Ф. Войно-Ясенецкого Красноярский государственный педагогический университет. В.П. Астафьева Красноярский институт железнодорожного транспорта, филиал ИрГУПС Политехнический институт Сибирского федерального университета Сибирский государственный технологический университет Сибирский государственный университет науки и технологий. академик М.Ф. Решетнева Сибирский институт бизнеса, управления и психологии Сибирский межрегиональный учебный центр Сибирский федеральный университет Торгово-экономический институт СФУ Юридический институт СибФУ Кременчугский национальный университет им.М. Остроградского Криворожский государственный педагогический университет Криворожский национальный университет Криворожский экономический институт КНЭУ. В. Гетьмана авиационно-технический колледж Курганская государственная сельскохозяйственная академия. Т. С. Мальцева Курганский государственный университет Курская государственная сельскохозяйственная академия. пр. И.И. Иванова Курский государственный медицинский университет Курский институт социального образования Региональный финансово-экономический институт Юго-Западный государственный университет Тувинский государственный университет Лесосибирский педагогический институт (филиал Сибирского федерального университета) Липецкий государственный педагогический университет Липецкий государственный технический университет Лужский институт (филиал Ленинградского государственного университета им.
.С. Пушкина) Луганская государственная академия культуры и искусств Луганский государственный медицинский университет Луганский государственный университет внутренних дел. Э.А. Дидоренко Луганский государственный университет. Владимир Даль Луганский национальный аграрный университет Луганский национальный университет им. Восточно-Европейский национальный университет имени Тараса Шевченко. Леси Украинки Луцкий национальный технический университет Львовская коммерческая академия Львовская национальная академия искусств Львовский государственный университет внутренних дел Львовский государственный университет физической культуры Львовский институт экономики и туризма Львовский национальный аграрный университет Львовский национальный медицинский университет им.Львовский национальный университет ветеринарной медицины и биотехнологии им. Д. Галицкого. С.З. Львовский национальный университет имени Гжицкого. И. Франко Львовская политехническая Российская таможенная академия Северо-Восточный государственный университет Ингушский государственный университет Магнитогорский государственный технический университет им.
Г.И. Носова Магнитогорский медицинский колледж им. ПФ. Надеждина Азовский морской институт Одесской национальной морской академии Донецкий государственный университет управления Мариупольский государственный университет Приазовский государственный технический университет Дагестанская государственная медицинская академия Дагестанский государственный педагогический университет Дагестанский государственный технический университет Дагестанский государственный университет Мелитопольский государственный педагогический университет им.Б. Хмельницкого Таврический государственный агротехнологический университет Белорусская государственная академия искусств Белорусская государственная академия музыки Белорусская государственная академия связи Белорусский государственный аграрно-технический университет Белорусский государственный медицинский университет Белорусский государственный педагогический университет им. М. Танка Белорусский государственный технологический университет Белорусский государственный университет Белорусский государственный университет информатики и радиоэлектроники Белорусский государственный университет культуры и искусств Белорусский государственный университет физической культуры Белорусский государственный экономический университет Белорусский национальный технический университет Институт информационных технологий БГУИР Институт пограничной службы Республика Беларусь Институт Современные знания им.
ЯВЛЯЮСЬ. Международный государственный экологический университет имени Широкова. Международный университет им. А. Д. Сахарова МИТСО Минский государственный высший радиотехнический колледж Минский государственный политехнический колледж Минский инновационный университет Минусинский колледж культуры и искусства им. А. Мерзлова Белорусско-Российский университет Могилевский государственный университет им. А. А. Кулешова Могилевский государственный университет продовольствия Мозырский государственный педагогический университет. И.П. Шамякина [Файлы без вуза] Академический Международный Институт Академический Юридический Институт Академия ГПС МЧС России Академия Стандартизации, Метрологии и Сертификации Академия Труда и Социальных Отношений Федерации Независимых Профсоюзов России Инженерная Академия Военно-Воздушных Сил.пр. Н.Э. Жуковского Всероссийская академия внешней торговли Министерства экономического развития РФ Всероссийский государственный университет кинематографии. С.А. Герасимова «ВГИК» Высшее театральное училище (институт) им.
Щепкина М.С. ГАПОУ Колледж предпринимательства № 11 Государственная академия славянской культуры Государственная классическая академия им. Государственный академический гуманитарный университет им. Маймонида Государственный институт русского языка. В ВИДЕ. А. С. Пушкина Государственный университет землеустройства Государственный университет управления Гуманитарный институт телевидения и радиовещания.М.А. Литовчина Институт восстановительной медицины Институт гуманитарного образования и информационных технологий Институт журналистики и литературного творчества Институт международного права и экономики им. А.С. Грибоедова рыночная экономика, социальная политика и право Институт текстильной и легкой промышленности МГУТУ Институт туризма и гостеприимства Институт управления и права Институт экономики и культуры Колледж градостроительства и сервиса № 38 Колледж многоуровневого профессионального образования РАНХиГС Литературный институт им.ЯВЛЯЮСЬ. Горького Медицинский институт повышения квалификации Медицинский колледж № 1 Международная академия бизнеса и управления Международный институт экономики и права Международный юридический институт МИРЭА — Российский технологический университет Московская академия астрологии Московская академия предпринимательства при Правительстве Москвы Московская академия экономики и права Московская государственная академия ветеринарной медицины и биотехнологии.
К.И. Скрябина Московская государственная академия водного транспорта Московская государственная академия коммунального хозяйства и строительства Московская государственная академия физической культуры Московская государственная консерватория.Московская государственная художественно-промышленная академия имени П. И. Чайковского. С.Г. Строганова Московская гуманитарно-техническая академия Московская финансово-юридическая академия Московский авиационный институт (национальный исследовательский университет) Московский автомобильно-дорожный государственный технический университет Московский архитектурно-строительный институт Московский архитектурный институт (государственная академия) Московский банковский институт Московский горный институт (филиал НИТУ «МИСиС») Московский городской педагогический университет Московский городской психолого-педагогический университет Московский городской университет управления Правительства Москвы Московский государственный агроинженерный университет им.В.П.
Горячкина Московский государственный гуманитарно-экономический университет Московский государственный гуманитарный университет им. Московский государственный индустриальный университет им. М.А. Шолохова Московский государственный институт индустрии туризма. Ю.А. Сенкевича Московский государственный институт электроники и математики (технический университет) Московский государственный колледж информационных технологий Московский государственный лингвистический университет Московский государственный инженерный университет «МАМИ» Московский государственный медико-стоматологический университет им. А.И. Евдокимова Московский государственный областной университет имени М.В. Ломоносова Московский государственный открытый университет имени В.С. Черномырдин Московский государственный строительный университет Московский государственный технический университет гражданской авиации Московский государственный технический университет им. Н.Э. Баумана Московский государственный технологический университет «Станкин» Московский государственный университет геодезии и картографии Московский государственный университет дизайна и технологий Московский государственный университет им.
М.В. Ломоносова Московский государственный университет инженерной экологии Московский государственный университет международных отношений Министерства иностранных дел России (МГИМО) Московский государственный университет полиграфии.И. Федорова Московский государственный университет пищевых производств Московский государственный университет приборостроения и информатики Московский государственный университет прикладных биотехнологий Московский государственный университет инженерной экологии Московский государственный университет путей сообщения Московский государственный университет технологий и управления им. КГ. Разумовского Московский государственный университет тонких химических технологий. М.В. Ломоносова Московский государственный университет экономики, статистики и информатики (МЭСИ) Московский государственный юридический университет им.О.Э. Кутафин Московский гуманитарно-экономический институт Московский гуманитарный институт им. Е. Р. Дашкова Московский гуманитарный университет Московский издательско-полиграфический техникум.
И. Федорова Московский институт государственного регулирования и права Московский институт предпринимательства и права Московский институт телевидения и радиовещания «Останкино» Московский международный университет Московский новый юридический институт Московский образовательный комплекс им. В. Талалихина Московский государственный педагогический университет Московский психолого-социальный университет Московский социально-экономический институт Московский технический университет связи и информатики Московский технологический институт «ВТУ» Московский университет им.С.Ю. Витте (бывший Московский институт экономики, управления и права) Московский университет МВД РФ. В.Я. Кикотя Московский финансово-промышленный университет Синергия Московский художественно-промышленный институт Московский экономический институт Музыкально-педагогический государственный институт им. мм. Ипполитова-Иванова Национальный институт бизнеса Национальный исследовательский технологический университет «МИСиС» Национальный исследовательский университет «Высшая школа экономики» Национальный исследовательский университет «МИЭТ» Национальный исследовательский университет «МЭИ» Национальный исследовательский ядерный университет (МИФИ) Открытый университет Израиля в СНГ Педагогический Институт физической культуры и спорта МГПУ Первый МГМУ им.
ИХ. Сеченовского политехнического колледжа имени П.А. Овчинникова Православный Свято-Тихоновский гуманитарный университет Российская академия музыки. Гнесиных Российская академия народного хозяйства и государственной службы при Президенте Российской Федерации Российская международная академия туризма Российская открытая академия транспорта МИИТ Российский государственный аграрный университет Московская сельскохозяйственная академия им. Тимирязева Российский государственный геологоразведочный университет. С. Орджоникидзе Российский государственный гуманитарный университет Российский государственный социальный университет Российский государственный технологический университет.К.Э. Циолковского (МАТИ) Российский государственный торгово-экономический университет Российский государственный университет имени А.Н. Косыгина Российский государственный университет инновационных технологий и предпринимательства Российский государственный университет нефти и газа. ИХ. Губкина Российский государственный университет юстиции Российский государственный университет туризма и сервиса Российский государственный университет физической культуры, спорта, молодежи и туризма (ГЦОЛИФК) Российский национальный исследовательский медицинский университет имени Н.
И. Пирогова Российский новый университет Российский университет дружбы народов Российский театральный университет Искусств Российский химико-технологический университет им.Д.И. Менделеева, Российский экономический университет. Г.В. Плеханова Столичная финансово-гуманитарная академия Театральный институт им. Б. В. Щукина в Государственном академическом театре. Е. Вахтангова Университет Российского инновационного образования Университет Российской академии образования Федеральный институт повышения квалификации и переподготовки кадров Финансовый университет при Правительстве Российской Федерации Школа-студия (институт) им. Вл. И. Немировича-Данченко во МХАТе. А. П.Чехова Мукачевский государственный университет Международный институт бизнес-образования Мурманский государственный гуманитарный университет Московский государственный университет леса Московский кооперативный колледж Альтшуля Российский университет кооперации Камская государственная инженерно-экономическая академия Набережночелнинский государственный торгово-технологический институт Набережночелнинский институт КФУ Набережные Челны Институт социально-педагогических технологий и ресурсов Кабардино-Балкарского государственного университета.
Х. Бербекова Нанкинский университет науки и технологии Нежинский государственный университет им.Н. Гоголя Немешаевский агротехнический колледж Нижневартовский государственный университет Нижнекамский химико-технологический институт Казанского государственного технологического университета Волжская государственная академия водного транспорта Нижегородская государственная консерватория им. М.И. Глинки Нижегородская государственная сельскохозяйственная академия Нижегородская юридическая академия Нижегородский государственный архитектурно-строительный университет Нижегородский государственный инженерно-экономический университет Нижегородский государственный лингвистический университет им. НА.Добролюбов Нижегородский государственный педагогический университет им. К. Минина Нижегородский государственный технический университет. Р.Э. Алексеева Нижегородский государственный университет. Н.И. Лобачевского Нижегородский институт управления и бизнеса Нижегородский институт управления РАНХиГС (ВВАГС) Приволжский исследовательский медицинский университет (бывший НижГМА) Нижнетагильский государственный социально-педагогический институт (филиал РГППУ) Нижегородский технологический институт (филиал УрФУ) Национальный университет им.
Судостроение.адм. Макарова Николаевский национальный аграрный университет Николаевский национальный университет им. В.А. Сухомлинского Черноморского государственного университета. Петра Могилы Новгородский государственный университет имени Ярослава Мудрого Нововолынский электромеханический техникум Новокузнецкий институт (филиал КемГУ) Сибирский государственный индустриальный университет Государственный морской университет им. Институт катализа им. адмирала Ф. Ф. Ушакова. Г.К. Боресков Новосибирская государственная консерватория. М.И. Глинки Новосибирский государственный аграрный университет Новосибирский государственный архитектурно-строительный университет Новосибирский государственный медицинский университет Новосибирский государственный педагогический университет Новосибирский государственный технический университет Новосибирский государственный университет Новосибирский государственный университет архитектуры, дизайна и искусств (бывший НГАХА) Новосибирский государственный университет экономики и управления Новосибирский медицинский Колледж Новосибирский юридический колледж Институт (филиал ТГУ) Сибирская академия финансов и банковского дела Сибирский государственный университет водного транспорта Сибирский государственный университет геосистем и технологий Сибирский государственный университет связи Сибирский государственный университет телекоммуникаций и информатики Сибирский институт управления РАНХиГС (СибАГС) Сибирский Университет потребительской кооперации Южно-Российский государственный университет Технический университет (Новочеркасский политехнический институт) (ЮРГТУ (НПИ)) Обнинский гуманитарный институт Обнинский институт атомной энергии НИЯУ МИФИ Курский колледж культуры Национального университета Одесская морская академия (бывш.
ОНМА) Национальный университет Одесская юридическая академия Одесская государственная академия строительства и архитектуры Одесская национальная академия пищевых технологий Одесская национальная академия связи. В ВИДЕ. Попов Одесский государственный аграрный университет Одесский государственный экологический университет Одесский государственный экономический университет Одесский корпоративный компьютерный колледж Одесский национальный медицинский университет Одесский национальный морской университет Одесский национальный политехнический университет Одесский национальный университет им. И.И. Мечникова Одесское областное базовое медицинское училище Южноукраинский национальный педагогический университет им.К.Д. Ушинского Озерский технологический институт Омская академия МВД России Омский государственный аграрный университет. П. А. Столыпина Омский государственный институт сервиса Омский государственный медицинский университет Омский государственный педагогический университет Омский государственный технический университет Омский государственный университет им.
Ф.М. Достоевского Омский государственный университет путей сообщения Омский экономический институт Омский юридический институт Сибирская государственная автомобильно-дорожная академия Сибирский государственный университет физической культуры и спорта Орловский государственный технический университет) Медицинский институт Орловского государственного университета Орловский государственный институт искусств и культуры Орловский государственный институт экономики и торговли Орловский филиал РАНХиГС Оренбургский государственный аграрный университет Оренбургский государственный институт управления Оренбургский государственный медицинский университет Оренбургский государственный педагогический университет Оренбургский государственный университет Оренбургский институт (филиал МГЮА им. Кутафина) Орский гуманитарно-технологический институт (филиал ОГУ) Орский медицинский колледж ГБПОУ Осташков Колледж Ошского технологического университета.акад. мм. Адышева Инновационный Евразийский университет Павлодарский государственный педагогический университет Павлодарский государственный университет им.
С. Торайгырова Педагогический институт им. В.Г. Белинский Пензенский государственный университет Пензенская государственная сельскохозяйственная академия Пензенский государственный технологический университет Пензенский государственный университет Пензенский государственный архитектурно-строительный университет Переяслав-Хмельницкий государственный педагогический университет им. Сковороды Г. С. Западно-Уральский институт экономики и права Пермская государственная академия искусств и культуры Пермская государственная сельскохозяйственная академия.Д. Н. Прянишникова Пермский государственный университет Фармацевтическая академия Пермский государственный гуманитарно-педагогический университет Пермский государственный медицинский университет. ак. Э.А. Вагнера Пермский государственный национальный исследовательский университет Пермский гуманитарно-технический институт Пермский институт экономики и финансов Пермский национальный исследовательский политехнический университет Карельская государственная педагогическая академия Петрозаводская государственная консерватория им.
А.К. Глазунов Петрозаводский государственный университет Северо-Казахстанский государственный университет им. М. Козыбаева Камчатский государственный технический университет Пинский государственный профессионально-технический колледж машиностроения Полесский государственный университет Полтавская государственная аграрная академия Полтавский национальный педагогический университет им.Козыбаева В.Г. Полтавский национальный технический университет имени Короленко. Ю. Кондратюк Полтавский университет экономики и торговли Украинская медицинская стоматологическая академия Псковский сельскохозяйственный колледж Псковский государственный университет Ленинградский государственный университет им. В ВИДЕ. Пушкина Санкт-Петербургский государственный аграрный университет Пятигорский государственный лингвистический университет Пятигорский государственный технологический университет Пятигорский медико-фармацевтический институт (филиал ВолгГМУ) Северо-Кавказский институт РАНХиГС (СКАГС) Режевский политехнический университет Международный экономико-гуманитарный университет им.
С. Демьянчука Национальный университет водного хозяйства и природопользования Ровенский государственный гуманитарный университет Рогачевский государственный педагогический колледж Академия архитектуры и искусств Южного федерального университета Донской государственный аграрный университет Донской государственный технический университет Институт сервиса и туризма (филиал ДГТУ) Институт кафедры менеджмента, бизнеса и права Ростовской государственной консерватории им. С. В. Рахманинова Ростовский государственный медицинский университет Ростовский государственный университет путей сообщения Ростовский государственный экономический университет «РИНХ» Ростовский институт защиты предпринимательства Ростовский юридический институт (филиал РПА МЮ) Южный федеральный университет Рыбинский государственный авиационный технический университет им.П. А. Соловьева Рыбинское речное училище. В И. Калашникова Рыбницкий филиал Приднестровского государственного университета. Рязанский государственный агротехнологический университет им.
Т.Г.Шевченко. П.А. Костычев Рязанский государственный медицинский университет. акад. И.П. Павлова Рязанский государственный радиотехнический университет Рязанский государственный университет им. С.А. Есенина Медицинский университет «РЕАВИЗ» Поволжская государственная социально-гуманитарная академия Поволжский государственный университет связи и информатики Самарская академия государственного и муниципального управления Самарская государственная академия культуры и искусств Самарская гуманитарная академия Самарский государственный архитектурно-строительный университет Самарский государственный медицинский университет Университет Самарский государственный технический университет Самарский государственный университет путей сообщения Самарский государственный экономический университет Самарский институт — аспирантура факультета приватизации и предпринимательства Самарского национального исследовательского университета им.ак. С.П. Королева (бывший СГАУ, СамГУ) Самаркандский государственный медицинский институт Академия русского балета.
И. Ваганова Академия управления городской средой, градостроительства и полиграфии Балтийская академия туризма и предпринимательства Балтийский государственный технический университет «ВОЕНМЕХ» им. Д.Ф. Устинова Балтийский гуманитарный институт Балтийский институт экологии, политики и права Военная академия связи им. СМ. Военно-космическая академия имени Буденного. Военно-медицинская академия им. А.Ф. Можайского.СМ. Кировский Восточно-Европейский институт психоанализа Государственная полярная академия Государственный университет морского и речного флота. ТАК. Макарова Институт специальной педагогики и психологии. Р. Валленберг Институт телевидения, бизнеса и дизайна Международный институт психологии и менеджмента Национальный государственный университет физической культуры, спорта и здоровья. ПФ. Лесгафта Национальный минерально-сырьевой университет «Горный» Национальный открытый институт России Первый Санкт-Петербургский государственный медицинский университет им.И. И. П. Павлова Санкт-Петербургский государственный университет путей сообщения им.
Императора Александра I Российский государственный гидрометеорологический университет Российский государственный педагогический университет. А.И. Герцена Российская христианская гуманитарная академия Санкт-Петербургская государственная академия ветеринарной медицины Санкт-Петербургская государственная академия театрального искусства Санкт-Петербургская государственная консерватория им. НА. Римского-Корсакова Санкт-Петербургская государственная медицинская академия. И.И. Мечникова Санкт-Петербургская государственная химико-фармацевтическая академияПетербургская государственная художественно-промышленная академия им. А.Л. Штиглица Санкт-Петербургский государственный архитектурно-строительный университет Санкт-Петербургский государственный институт психологии и социальной работы Санкт-Петербургский государственный лесотехнический университет им. В.И. СМ. Кирова Санкт-Петербургский государственный морской технический университет Санкт-Петербургский государственный педиатрический медицинский университет Санкт-Петербургский государственный политехнический университет Машиностроительный институт Санкт-Петербургский государственный технологический институт (технический университет) Санкт-ПетербургСанкт-Петербургский государственный технологический университет растительных полимеров Санкт-Петербургский государственный торгово-экономический университет Санкт-Петербургский государственный университет Санкт-Петербургский государственный университет аэрокосмического приборостроения Санкт-Петербургский государственный университет гражданской авиации Санкт-Петербургский государственный университет информационных технологий, механики и Оптика Санкт-Петербургский государственный университет кино и телевидения Санкт-Петербургский государственный университет культуры и искусств Санкт-Петербургский государственный университет низкотемпературных и пищевых технологий Санкт-ПетербургСанкт-Петербургский государственный университет сервиса и экономики Санкт-Петербургский государственный университет связи.
проф. М.А. Бонч-Бруевич Санкт-Петербургский государственный университет технологий и дизайна Санкт-Петербургский государственный экономический университет (бывший ФИНЭК, ИНЖЭКОН) Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» Санкт-Петербургский гуманитарный университет профсоюзов Санкт-Петербургский институт внешнеэкономической деятельности Отношения, экономика и право Санкт-Петербургский институт гостеприимства Санкт-Петербургский институт управления и права Санкт-ПетербургСанкт-Петербургский политехнический университет Петра Великого (бывший Санкт-Петербургский государственный политехнический университет) Санкт-Петербургский университет Государственной противопожарной службы МЧС России Санкт-Петербургский университет МВД России Санкт-Петербургский университет им. Управление и экономика Санкт-Петербургский юридический институт Академии Генеральной прокуратуры Российской Федерации Санкт-Петербургский институт гуманитарного образования Северо-Западный государственный заочный технический университет Северо-Западный государственный медицинский университет им.
И.И. Мечникова Северо-Западный институт управления РАНХиГС (СЗАГС) Смольный институт Российской академии образования Мордовский государственный педагогический институт им. М.Е. Евсевьева Мордовский государственный университет имени А.И. Н. П. Огарёва Поволжский институт их управления. П.А. Столыпина РАНХиГС (ПАГС) Саратовская государственная консерватория. Л. В. Собинова Саратовская государственная юридическая академия Саратовский государственный аграрный университет. Н.И. Саратовский государственный медицинский университет имени Вавилова. В И. Разумовский Саратовский государственный технический университет.Ю.А. Гагарина в Саратовском государственном университете. Н.Г. Чернышевского Саратовский социально-экономический институт РЭУ им. Плеханова (бывший СГЭУ) Саровский государственный физико-технический институт Сахалинский государственный университет Севастопольский городской гуманитарный университет Севастопольский государственный университет Севастопольский национальный университет атомной энергии и промышленности Институт судостроения и морской арктической техники (Севмашвтуз) (филиал САФУ) Восточноукраинский национальный университет им.
В. Даля Северский Технологический институт НИЯУ МИФИ им. Шакарима Государственный университет г. Семей Казахский гуманитарно-правовой инновационный университет Московская Духовная академия Академия биоресурсов и природопользования Академия строительства и архитектуры (филиал КФУ) Гуманитарно-педагогическая академия (филиал КФУ) Крымский инженерно-педагогический Университет Крымский университет культуры, искусств и туризма Крымский федеральный университет им.В И. Медицинская академия Вернадского. С.И. Георгиевского Симферопольский университет экономики и управления Таврическая академия (филиал КФУ) Таврический национальный университет им. В И. Вернадского Донбасский государственный педагогический университет Смоленская государственная сельскохозяйственная академия Смоленский государственный институт искусств Смоленский государственный медицинский университет Смоленский государственный университет Смоленский гуманитарный университет Сосновский сельскохозяйственный колледж Сочинский государственный университет Сочинский институт Российский университет дружбы народов Северо-Кавказский гуманитарно-технический институт Северо-Кавказский федеральный университет Ставропольский государственный аграрный университет Университет Ставропольский государственный медицинский университет Ставропольский государственный педагогический институт Старооскольский технологический институт (филиал НИТУ «МИСиС») Стахановский учебно-научный институт горных и образовательных технологий Стерлитамакская государственная педагогическая академия Муромцевский лесотехнический техникум Сумской государственный педагогический университет им.
Макаренко Сумской государственный университет Сумской национальный аграрный университет Украинская академия банковского дела Национального банка Украины Сургутский государственный педагогический университет Сургутский государственный университет Сургутский институт нефти и газа (филиал Тюменского индустриального университета) Коми республиканская академия государственной службы и управления Сыктывкарская государственная Университет. Питирим Сорокина Сыктывкарский лесотехнический институт (филиал СПбГЛТА) Инженерно-технологическая академия ЮФУ Таганрогский институт им. Тамбовский государственный технический университет им. А.П. Чехова Тамбовский государственный университет им.Г.Р. Державин Тамбовский колледж экономики и предпринимательства Тамбовский филиал РАНХиГС (ПАГС им. Столыпина) Таразский государственный университет им. М.Х. Институт биоорганической химии им. Дулати. А. Садыкова Ташкентский государственный стоматологический институт Ташкентский университет информационных технологий Ташкентский химико-технологический институт Тверская государственная сельскохозяйственная академия Тверской государственный медицинский университет Тверской государственный технический университет Тверской государственный университет Тверской институт экологии и права Тверской медицинский колледж Тернопольский государственный медицинский университет им.
И. И. Горбачевского Тернопольский национальный педагогический университет им. В. Гнатюк Тернопольский национальный технический университет имени В.И. И. Пулюй Тернопольский национальный экономический университет Приднестровский государственный университет им. Т.Г. Шевченко Тобольский государственный педагогический институт. Д.И. Менделеева Поволжский университет. В.Н. Татищева Поволжский государственный университет сервиса Тольяттинский государственный университет Сибирский государственный медицинский университет Томский государственный архитектурно-строительный университет Томский государственный педагогический университет Томский государственный университет Томский государственный университет систем управления и радиоэлектроники Томский институт бизнеса Томский политехнический университет Южно-Уральский институт ветеринарной медицины Государственный аграрный университет (бывш.УГАВМ) Тульский государственный педагогический университет. Л.Н. Толстой Тульский государственный университет Международный казахско-турецкий университет им.
Х. А. Яссави Государственный аграрный университет Северного Зауралья Тюменская государственная академия культуры, искусств и социальных технологий Тюменская государственная академия мировой экономики, управления и права Тюменский государственный архитектурно-строительный университет Тюменский государственный медицинский университет Тюменский государственный нефтегазовый университет Тюменский государственный университет Закарпатский государственный университет Ужгородский национальный университет Восточно-Сибирская государственная академия культуры и искусств Восточно-Сибирский государственный университет технологий и управления Институт авиационной техники и управления (филиал УлГТУ) Ульяновская государственная сельскохозяйственная академия.П.А. Столыпина Ульяновский государственный педагогический университет им. Ульянова Ульяновский государственный технический университет Ульяновский государственный университет Ульяновский институт гражданской авиации имени Главного маршала авиации Б.
П. Бугаев Ульяновское высшее авиационное училище гражданской авиации Уманский государственный педагогический университет им. П. Тычина Уманский национальный университет садоводства Западно-Казахстанский аграрно-технический университет им. Западно-Казахстанский государственный университет имени Жангир хана. М. Утемисова Усинский политехнический колледж Приморская государственная сельскохозяйственная академия Уссурийский колледж технологий и менеджмента педагогического факультета ДВФУ Восточно-Казахстанский государственный технический университет им.Восточно-Казахстанский государственный университет им. Д. Серикбаева. С. Аманжолова Башкирская академия государственной службы и управления при Президенте Республики Башкортостан Башкирский государственный аграрный университет Башкирский государственный медицинский университет Башкирский государственный педагогический университет им. М. Акмулла Башкирский государственный университет Восточная экономико-правовая гуманитарная академия Уфимская государственная академия искусств им.
З. Исмагилова Уфимский государственный авиационный технический университет Уфимский государственный нефтяной технический университет Уфимский государственный университет экономики и сервиса Ухтинский государственный технический университет Тюменский государственный индустриальный университет Дальневосточный государственный гуманитарный университет Дальневосточный государственный медицинский университет Дальневосточный государственный университет путей сообщения Дальневосточный институт управления РАНХиГС ( ДВАГС) Дальневосточный юридический институт МВД России Тихоокеанский государственный университет Хабаровский государственный институт искусств и культуры Хабаровский государственный университет экономики и права Хабаровский институт инфокоммуникаций (филиал СибГУТИ) Ханты-Мансийская государственная медицинская академия Югорский государственный университет Национальный Аэрокосмический университет имени Н.Е. Жуковского Национальный технический университет Харьковский политехнический институт итут Национальный университет гражданской защиты Украины Национальный фармацевтический университет Национальный юридический университет им.
Ярослава Мудрого Украинская государственная академия железнодорожного транспорта Украинская инженерно-педагогическая академия Харьковская государственная академия дизайна и искусств Харьковская государственная академия культуры Харьковская государственная академия физической культуры Харьковская государственная ветеринарная академия Харьковская гуманитарно-педагогическая академия Харьковский государственный университет питания и торговли Харьковский гуманитарный университет Украинская народная академия Харьковский институт банковского дела УБД НБУ Харьковский финансовый институт (филиал УГУФМТ) Харьковский национальный автомобильно-дорожный университет Харьковский национальный аграрный университет им.В.В. Докучаева Харьковский национальный медицинский университет Харьковский национальный педагогический университет им. Сковороды Г. С. Харьковский национальный технический университет сельского хозяйства. П. Василенко Харьковский национальный университет внутренних дел Харьковский национальный университет городского хозяйства им.
А.Н. Бекетова Харьковский национальный университет. Харьковский национальный университет искусств имени В. Н. Каразина. И.П. Котляревского Харьковский национальный университет радиоэлектроники Харьковский национальный университет строительства и архитектуры Харьковский национальный экономический университет им.С. Кузнеца Харьковский патентно-компьютерный колледж Харьковский торгово-экономический институт (филиал КНТЭУ) Херсонская государственная морская академия Херсонский государственный аграрный университет Херсонский государственный университет Херсонский национальный технический университет юридический Худжандский государственный университет Чайковский государственный институт физической культуры Чайковский технологический институт (филиал ИжГТУ) Чебоксарский кооперативный институт (филиал РУК) Чувашская государственная сельскохозяйственная академия Чувашский государственный педагогический университет им. И. Яковлев Чувашский государственный университет им.В. Ульянова Российско-Британский институт менеджмента Уральский государственный университет физической культуры Уральский социально-экономический институт Академии труда и социальных отношений ФНПР Челябинская государственная агроинженерная академия Челябинская государственная академия культуры и искусств Челябинский государственный педагогический университет Челябинский государственный университет Челябинский институт экономики и Закон.
М.В. Ладошина Челябинский филиал РАНХиГС (УРАГС ЧФ) Челябинский юридический институт МВД России Южно-Уральский государственный медицинский университет Минздрава России (бывший ЧелГМА) Южно-Уральский государственный университет Южно-Уральский институт управления и экономики Южно-Уральский профессиональный институт Саяно-Шушенский филиал Сибирского федерального университета Черемховский медицинский колледж Институт управления и информационных технологий (филиал Санкт-Петербургского государственного университета им.Санкт-Петербургский государственный политехнический университет) Череповецкий государственный университет Черкасский государственный технологический университет Черкасский институт пожарной безопасности имени Героев Чернобыля Черкасский национальный университет им. Б. Хмельницкого Черниговский государственный институт экономики и управления Черниговский национальный педагогический университет им. Т.Г. Шевченко Черниговский национальный технологический университет Буковинский государственный медицинский университет Черновицкий национальный университет им.
Ю. Федьковича Чистопольский филиал «Восток» Казанского национального исследовательского технического университета имени А.Н. Туполева — КАИ Забайкальский аграрный институт (филиал ИрГСХА) Забайкальский государственный университет Забайкальский институт железнодорожного транспорта, филиал ИрГУПС Читинская государственная медицинская академия Читинский институт Байкальского государственного университета экономики и права Шадринский государственный педагогический институт Институт сервиса и предпринимательства ДГТУ Юг Российский гуманитарный институт Университет Мирас Южно-Казахстанская медицинская академия Южно-Казахстанский государственный университет им. М. Ауэзов Калмыцкий государственный университет Энгельсский технологический институт Юргинский технологический институт Томского политехнического университета Северо-Восточный федеральный университет им.М.К. Аммосова Международный университет бизнеса и новых технологий Ярославская государственная сельскохозяйственная академия Ярославский государственный медицинский университет Ярославский государственный педагогический университет им.