Квантовый компьютер и биткоин – Опасен ли квантовый компьютер для Биткойна? |

Опасен ли квантовый компьютер для Биткойна? |

Благодаря недавней утечке от Сноудена, мы узнали, что Агентство Национальной Безопасности (АНБ) строит квантовый компьютер. Газета «Вашингтон Пост» опубликовала историю под довольно сенсационным заголовком — «АНБ ищет возможности построить квантовый компьютер, который сможет взломать большинство типов шифрования».

Естественно, это вызвало большой интерес на основных биткойн-форумах, а также в посвященных Биткойну группах на Reddit и Facebook. На самом же деле, мы не узнали ничего особо нового. О соответствующем проекте АНБ было известно давно, различные виды квантовых вычислений интересуют их изначально. Мы знаем, что на этот проект был выделен бюджет в 79.7 миллиона долларов США, но реальные достижения по-прежнему очень малы. И, как правильно заметил один из комментаторов:  «Никогда не поверю, что АНБ уже получила в своё распоряжение нечто подобное, и никто в мире об этом не узнал».

Что это за кубиты такие?

Тем не менее, воспользуемся случаем и обсудим перспективы квантовых вычислений применительно к Биткойну. Позвольте мне привести маленький пример для тех, кто не особенно в курсе квантовых вычислений и недоумевает: о чем, собственно, речь? Современные компьютеры имеют дело с информацией в виде битов — бинарных цифр, только «0» или «1». Эти биты обычно хранятся на жёстких дисках ваших компьютеров. В этом случае они представляют собой полярность намагничивания крошечных частиц магнитного диска.  Если же данные хранятся в оперативной памяти или флеш-памяти, они кодируются двумя различными уровнями заряда мини-конденсатора.

Строка битов может нести информационное наполнение, полезное для человека. Например, 01000001 соответствует букве «A» в расширенной таблице ASCII. При любых расчетах с битами делается одна операция за раз.

Основанные на фотонах квантовые компьютеры используют различные состояния квантовых частиц, чтобы получить так называемые «квантовые биты» (кубиты). Например, фотон, который вращается по вертикальной оси, может обозначать «1», а при вращении по горизонтальной оси фотон будет обозначать «0». В отличие от обычных битов, которые могут представлять лишь значения «0» или «1», но не то или другое сразу, кубиты обладают одним довольно странным свойством, которое называется  «суперпозиция». Оно означает, что лежащий в основе кубита фотон может вращаться по всем осям —

одновременно. То есть кубит может в моменте представлять значение и 0, и 1, и любое их сочетание. Не спрашивайте меня, как именно, это может объяснить разве что профессор квантовой физики, да и то не каждый день.

Это свойство приводит к коренным различиям между обычными и квантовыми вычислениями. Обычный компьютер может выполнить всего одну операцию за один раз. А квантовый компьютер (теоретически) за то же время выполнит миллионы вычислений. То есть при переходе к квантовым вычислениям вычислительная мощность должна существенно возрасти. Однако квантовые вычисления также имеют свои ограничения.

Когда журналисты пишут нечто вроде: «В этом помещении металлические ящики размером с комнату гасят все электромагнитные колебания. Именно здесь Агентство Национальной Безопасности  ускоренно строит свой компьютер. Против него — ничто все шифры, которые используются в медицине, страховании, бизнесе, финансах, разведке и военном деле», это заставляет людей думать, что не за горами конец криптографии, какой мы её знаем. Но, к счастью, это не соответствует действительности.

Атака перебором: силенок не хватит

Рассмотрим атаку, которая приходит на ум большинству людей при упоминании квантовых компьютеров — атаку путём простого перебора (bruteforce). Это значит, что вы раз за разом пробуете все возможные ключи, пока не получите правильный. Если у вас есть достаточно времени, вы можете подобрать любой пароль. Проблема состоит в том, что при обычных вычислениях потребуются многие миллиарды, нет, триллионы лет вычислений самого новейшего суперкомпьютера, чтобы получить нужный ключ путём перебора. Но, может быть, квантовый компьютер сделает это быстрее?

Обратимся к книге известного эксперта Брюса Шнайера «Прикладная Криптография»:

Одно из следствий из второго закона термодинамики состоит в том, что для представления единицы информации нужно определённое количество энергии.
Запись единичного бита путём изменения состояния системы потребует энергии не менее чем kT, где «T» это абсолютная температура системы и «k» это константа Больцмана.

При постоянной k = 1.38×10^-16 эрга/°Кельвин, и средней температуре во Вселенной в 3.2° Кельвина, наш идеальный компьютер будет работать при 3.2°K. При этом он будет потреблять 4.4×10

-16 эрга каждый раз, когда он изменит состояние одного бита. Запуск компьютера при температурах более низких потребует дополнительного расхода энергии для теплового насоса.

Годовая энергия, излучаемая Солнцем, равняется 1.21×10⁴¹ эрга. Этого достаточно, чтобы обеспечить 2.7×10⁵⁶ переключений бита идеального компьютера; то есть, этого достаточно для перебора 187-битного шифрования за год. Хорошо. Предположим, мы построим сферу Дайсона вокруг Солнца и будем улавливать и копить ВСЮ солнечную энергию 32 года подряд, без каких любо потерь. В этом случае, мы сможем обеспечить энергией компьютер, который позволит нам досчитать до 2

192. Заметим, что это мы просто перебираем биты. У нас не останется энергии ни на что другое, чтобы совершать с этими битами хоть какие-либо полезные вычисления.

Предположим, мы не ограничимся и нашим Солнцем. Обычная сверхновая дает что-то вроде  10⁵¹ эрг (при этом в сотни раз большее количество энергии выделяется в виде нейтрино, её мы не учитываем из-за практических сложностей конвертации этой энергии). Если вся эта энергия пойдёт на одну сверхбольшую вычислительную оргию, мы сможем перебрать 219-битный ключ полностью, от начала и до конца.

Эти цифры не имеют ничего общего с технологией реальных устройств; это просто максимум перебора при идеальной эффективности, которую позволяют нам законы термодинамики. Они показывают нам, что атака перебором на  256-битный ключ неосуществима, пока компьютеры делаются из обычной материи и находятся в нашем пространстве.

Таким образом, если даже нам удастся собрать всю без остатка энергию, которая выделяется при взрыве Сверхновой, и всю без остатка направить её в наш идеальный компьютер — нам не удастся получить подбор даже одного обычного 256-битного ключа шифрования.

Речь, однако, не идет о простом переборе — атака на коммерческие алгоритмы шифрования подразумевает атаку на лежащую в их основе математику.

Подрываем основы математики

Сегодня большинство алгоритмов шифрования с открытым ключом опираются на алгоритм «целочисленной факторизации» (RSA) или «дискретные логарифмы» (DSA, а также криптография на эллиптических кривых). В 1994 математик Питер Шор продемонстрировал эффективный квантовый алгоритм для решения задач факторизации и вычисления дискретных логарифмов. Этот алгоритм позволит довольно эффективно раскрывать шифрование с открытым ключом при использовании квантового компьютера. Но это не относится ко всем видам криптографии. Скажем, криптография с симметричным ключом, а также криптографические функции хэширования находятся вне зоны действия квантовых алгоритмов поиска.

Биткойн использует сразу несколько криптографических алгоритмов: алгоритм цифровой подписи на эллиптической кривой (ECDSA) для подписи транзакций и две хэширующие функции —  SHA-256 и RIPEMD160. Если АНБ в итоге преуспеет в создании применимого для нужд криптографии квантового компьтера, ECDSA будет скомпрометирован, в то время как  SHA-256 и RIPEMD160 по-прежнему сохранят свои защитные функции.

Хорошие новости состоят в том, что ECDSA, если он будет скомпрометирован, можно сравнительно легко заменить чем-то другим. Гораздо хуже, если удастся подобрать ключ к SHA-256. Напомним, что согласно устройству сети Биткойн, именно SHA-256 используется в процессе Биткойн-майнинга.

На сегодняшний день, миллиарды долларов вложены в чипы, которые не делают ничего, кроме вычислений SHA-256. Если SHA-256 потеряет актуальность, такие востребованные сейчас чипы и основанные на них ASIC-майнеры станут просто никому не нужным железом. Катастрофические последствия возникнут, если это произойдёт внезапно, и ни у кого не будет времени подготовиться. Ведь безопасность сети Биткойн полагается на сложность и дороговизну проведения атаки, позволяющей захватить 51% вычислительной мощности сети. Внезапная замена хэш-функции (скажем, на Scrypt, или что-то другое) приведет к серьезному падению безопасности сети на время переходного периода.

Но хотя (теоретически) какие-то угрозы для SHA-256 и могут существовать, применение квантовых компьютеров, к счастью, к ним совершенно не относится.

Шеф, усё пропало?

Давайте вернёмся к ECDSA, который может быть теоретически взломан достаточно мощными квантовыми компьютерами. Этот алгоритм генерирует пару ключей:  закрытый/открытый ключ.

Пользуясь Биткойном, вы держите свой закрытый ключ в секрете и используете его только для подписи своих транзакций. Эта подпись свидетельствует для биткойн-сети, что биткойны пытается перевести именно законный владелец данного биткойн-адреса. Сеть проверяет вашу подпись, сравнивая её с открытым ключом.  Работающий мощный квантовый компьютер теоретически позволит АНБ получить ваш закрытый ключ из открытого ключа. Так что же — это значит, что АНБ может добраться до наших биткойнов?!

Не совсем так.

В случае Биткойна, ваш «открытый ключ» изначально не является таким уж открытым. Вместо него используется так называемый «биткойн-адрес», который представляет собой лишь хэш открытого ключа. Предоставляя свой биткойн-адрес другим людям, чтобы они вам отправили средства, вы даёте им только хэш вашего открытого ключа, но не сам ключ. Хэш — это результат работы криптографической функции хэширования. Данная функция является односторонней и не может быть взломана квантовым компьютером.

Мы называем эту функцию односторонней, так как она не дает возможность получить исходную информацию на основе выходной. Нечто вроде шифрования чего-либо, после чего ключ от шифра теряется. Чтобы показать это, давайте подсчитаем хэш RIPEMD160 фразы «Привет Мир”.

Привет Мир ==> a830d7beb04eb7549ce990fb7dc962e499a27230

Адрес биткойна рассчитывается путем пропускания вашего открытого ключа сразу через несколько криптографических функций хеширования:

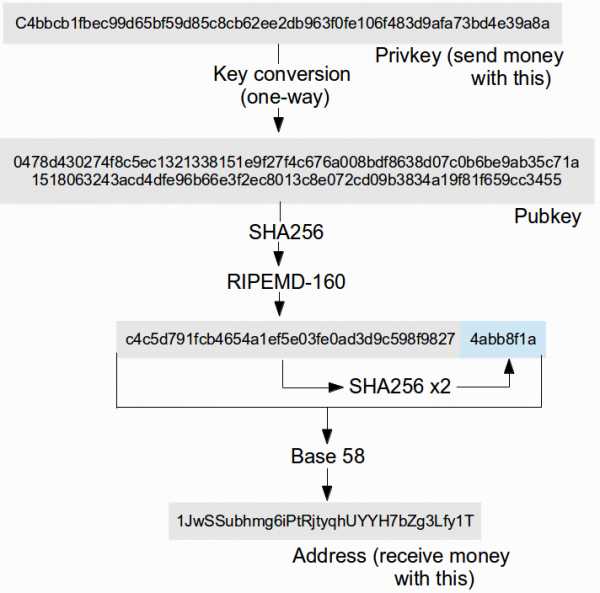
Проще говоря, атакующий с мощным квантовым компьютером может получить закрытый ключ из открытого ключа, но не может получить сам открытый ключ из биткойн-адреса. Ведь биткойн-адрес проходит через несколько однонаправленных хэш функций, устойчивых против квантовых вычислений.

Однако вы все же должны однажды транслировать ваш открытый ключ в сеть — когда вы подписываете транзакцию. Иначе сеть не сможет подтвердить сделку, ведь нет никакого другого способа проверить вашу подпись. Это, однако, не конец света — это говорит лишь о том, что гипотетический квантовый компьютер АНБ превращает все биткойн-адреса в одноразовые.
Всякий раз при совершении транзакции вам придётся отправлять все оставшиеся биткойны на новый адрес, ведь открытый ключ старого становится при транзакции известен, и теоретически может быть взломан.

Если вы не переместите баланс с этого прежнего адреса, АНБ может при помощи квантового компьютера подобрать к нему секретный ключ и украсть всё, что на нём есть. Хотя это и будет не совсем удобно для пользователей, биткойн-разработчики в любом случае получат достаточно времени, чтобы заменить ECDSA на одну из устойчивых к квантовым расчётам схем цифровой подписи, например, подпись Лэмпорта.

Морально Квантово устойчивые подписи

В этом разделе немало технических подробностей. Надеюсь, они не будут слишком сложны для начинающих. Существует несколько различных типов устойчивого к квантовым расчётам шифрования с открытым ключом: на основе матрицы, на основе кода, многомерные квадратичные функции, и функции хэширования. Как я уже упоминал, предполагается, что функции хэширования окажутся квантово устойчивыми. Это дает нам возможность построить устойчивую к квантовым вычислениям замену для  ECDSA с использованием только функций хэширования. Поскольку эти функции близки и привычны любому биткойн-майнеру, давайте взглянем для начала на основанные на хэшировании системы. Это интересно ещё и тем, что их сравнительно легко понять, а описанные ниже функции хэширования широко используются на практике.

Схема одноразовой подписи Лэмпорта (LOTSS)

Для начала мы возьмем хэширующую функцию длиной  в 160-бит, чтобы обеспечить должную безопасность. RIPEMD160 или SHA-1 вполне подойдут. Чтобы получить пары открытый/закрытый ключ, мы создадим 160 пар случайных чисел (320 чисел всего). Этот набор случайных чисел будет служить нашим секретным ключом.

Пара#	Закрытый ключ
1	e9e515b332cf1ce01299497e9e94b7df353ff022 ce56dcfdb7038e6ab0b37c383dbfda8cb45d60ea
2	811f71c5cf7639a40df7b9b187bf768016791cf8 1094b13455a133d2d11898cfa30916e12be3e0ab
…	…
159	bc6a1eb98148850dd2b32ae632005f5472c06a70 c10f4ac3d645d891d9b5dc0fa0b7294ad14ac3df
160	585801c9da7ce0d562f375338b456ba9f10be3f6 3c3363ed7273f1ef9c1aed3fc5a7433002b668f8

Теперь, генерируем открытый ключ. Для этого мы возьмём хэш RIPEMD160 каждой из 320 случайных чисел (я сократил их наполовину так, чтобы они поместились в таблице).

Пара#	Закрытый ключ	Открытый ключ
1	e9e515b332cf1ce01299 ce56dcfdb7038e6ab0b3	d7c3e127380fbbbe37b9 4ddf29fb200aa0fd90b1
2	811f71c5cf7639a40df7 1094b13455a133d2d118	f84a8e5a0dce682e48c5 4a88310f694329b9ab97
…	…	…
159	bc6a1eb98148850dd2b3 c10f4ac3d645d891d9b5	7d5c0e19c4dc9077be6c ffbbe97612e581f073b6
160	585801c9da7ce0d562f3 3c3363ed7273f1ef9c1a	38ed36c30ee72c95c598 a546f885e8210c61767d

А сейчас мы подпишем некий текст подписью Лэмпорта. Для этого мы сначала создадим дайджест этого текста, хэшировав его с помощью RIPEMD160 (в Биткойне используется этот же алгоритм для хэширования транзакции), и транслируем полученный результат в двоичный код. Мы и в этот раз используем «Привет Мир» в качестве примера.

Привет Мир ==> a830d7beb04eb7549ce990fb7dc962e499a27230 ==> 1010100000110000110101111011111010110000010011101011011101010100100111001110100110010000111110110111110111001001011000101110010010011001101000100111001000110000

Далее мы последовательно сопоставим двоичные цифры полученного кода с парами чисел из закрытого ключа (предыдущая таблица). Если бит равен 0, мы добавим первое число к цифровой подписи, а если он равен 1, то второе.

Пара#	Дайджест	Открытый ключ	Подпись
1	1	e9e515b332cf1ce01299 ce56dcfdb7038e6ab0b3	ce56dcfdb7038e6ab0b3
2	0	811f71c5cf7639a40df7 1094b13455a133d2d118	811f71c5cf7639a40df7
…	…	…	…
159	0	bc6a1eb98148850dd2b3 c10f4ac3d645d891d9b5	bc6a1eb98148850dd2b3
160	0	585801c9da7ce0d562f3 3c3363ed7273f1ef9c1a	585801c9da7ce0d562f3

Наконец, чтобы проверить действительность подписи, мы сначала создадим дайджест текста, используя описанную выше процедуру. После этого надо взять хэш каждого из 160 чисел в цифровой подписи при помощи RIPEMD160. Наконец, достаточно сравнить эти хэши с соответствующими числами из открытого ключа — если они совпадают, то цифровая подпись правильная.

Пара#	Хэш подписи	Дайджест	Открытый ключ
1	4ddf29fb200aa0fd90b1	1	d7c3e127380fbbbe37b9 4ddf29fb200aa0fd90b1
2	f84a8e5a0dce682e48c5	0	f84a8e5a0dce682e48c5 4a88310f694329b9ab97
…	…	…	…
159	7d5c0e19c4dc9077be6c	0	7d5c0e19c4dc9077be6c ffbbe97612e581f073b6
160	38ed36c30ee72c95c598	0	38ed36c30ee72c95c598 a546f885e8210c61767d

Вот мы и добились желаемого — получили схему цифровой подписи, устойчивую к квантовым вычислениям. При этом мы использовали только хэш-функции.

Только тот, у кого есть доступ ко всем 320 случайным цифрам приватного ключа, сможет генерировать цифровую подпись, хэши которой совпадут с числами из открытого ключа, определяемыми дайджестом текста. Правда, на практике использование этой схемы сталкивается с проблемами. Во-первых, как следует из названия, схема одноразовой подписи Лэмпорта может использоваться только один раз. Причина этого в том, что вы по сути теряете половину секретного ключа с каждой подписью. Если вы подпишете несколько сообщений одним ключом, то полностью скомпрометируете свою подпись. Так как мы рассматриваем этот алгоритм применительно к Биткойну, то каждый биткойн-адрес можно будет использовать только один раз, увы.

Не меньшей проблемой является то, что размеры ключей и подписи крайне велики. И закрытый, и открытый ключ занимают аж по 6400 байтов. Сравните — 32 и 64 байта для закрытого и открытого ключей ECDSA. И подпись занимает 3200 байтов, а не 71-73 байта. Биткойн уже и так имеет проблемы с масштабируемостью. Повышение размеров ключа и подписи только усугубит эту проблему.

Правда, приватный ключ Лэмпорта можно значительно уменьшить в размере, используя генерацию случайных цифр из одного набора. Для этого мы используем RIPEMD160 (размер набора + n), где n первоначально установлено в 1 и последовательно увеличивается до 320.

К сожалению, размер закрытого ключа не настолько важен, как размер открытого ключа и подписи. Существует ещё одна подобная схема одноразовой подписи под названием «подпись Винтерница». Она имеет потенциал для снижения размера ключа, но не за счёт снижения сложности хэширующих операций. К счастью, это ещё не всё, что у нас есть.

Схема подписи Мёркле (MSS)

Схема подписи Мёркле объединяет в себе схему одноразовой подписи (неважно, схему Лампорта или Винтерница) с деревом Мёркле (также известным как дерево хэшей). Это позволяет нам подписать одним открытым ключом несколько сообщений, не создавая ущерба их безопасности. Давайте посмотрим, как это работает.

Мы начнём с создания пар ключей Лампорта. Количество ключей, которые нам понадобится, будет равно числу подписей, которые мы хотим получить из одного открытого ключа. Давайте, например, возьмём восемь подписей. Затем мы вычислим дерево Мёркле с помощью каждого из восьми открытых ключей Лампорта. Чтобы сделать это, объединим открытые ключи попарно. Затем полученные хэши перемешиваются и хэшируются снова. Этот процесс чем-то похож на определение победителя футбольного чемпионата.

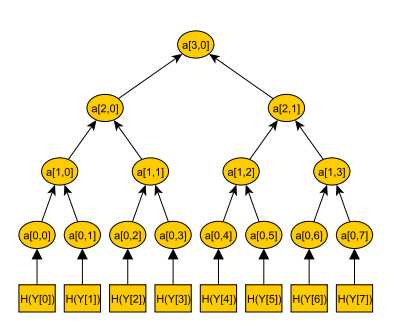Хэш находится на самом верху дерева (дерева Мёркле), в то время как корнем дерева является открытый ключ Мёркле. Это заметно сокращает размер открытого ключа — с 6400 байтов, необходимых для подписи Лампорта до длины одного RIPEMD160 хэша — 20 байт.

Для расчёта подписи, вам нужно выбрать пару ключей Лампорта и подписать послание дайджестом, так же, как и раньше. На этот раз, сопоставляя подпись Лампорта с одним из листьев дерева Мёркле, мы доберемся до открытого ключа, то есть до корня дерева.

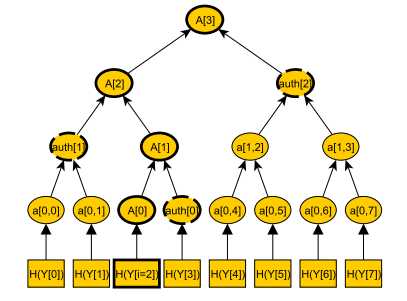Для схемы, приведённой выше, подписью будет:

sig′||H(Y[i=2])||A[0]||auth[0]||A[1]||auth[1]||A[2]||auth[2]||A[3]

Для проверки подписи Мёркле достаточно просто проверить подпись Лампорта, а затем убедиться, что хэш листьев дерева Мёркле соответствует хэшу публичного ключа. Если это так, подпись действительна.

У данной схемы есть ряд преимуществ по сравнению с LOTSS. И открытый, и закрытый ключи сокращены с 6400 байт до 20 байт. Таким образом, вы можете создать несколько подписей для одного открытого ключа.

Но есть небольшая и важная поправка. Чем больше сообщений вы хотите подписать вашим открытым ключом, тем большее дерево Мёркле вам нужно. Чем больше размер дерева, тем больше размер подписи. В конце концов, подпись станет непрактично большой. Особенно это актуально в случае использования для  Биткойна. Это приводит нас к финальной версии криптографии, устойчивой к квантовым расчётам. Давайте, наконец, обсудим её.

Святой Грааль криптографии: CMSS/GMSS

Устойчивая к квантовым расчётам криптография MSS известна уже более 30 лет. Она, по сути, осталась невредимой, несмотря на интенсивный криптоанализ. Однако большинство улучшений этой схемы произошли в последние пять лет. Наиболее перспективно выглядят две схемы парной подписи, разработанные группой Дахмена, Клицевич и Бахмана.

Эти схемы — улучшенная схема подписи Мёркле (CMSS) и обобщённая схема подписи Мёркле  (GMSS).

Поскольку эти исследования криптографов довольно новые, в популярной литературе и на Википедии они пока толком не освещены. Для особо упорных, ссылки на академические исследования вы можете найти здесь и здесь. Двое из криптографов, разрабатывавших эти схемы подписи, являются авторами учебника по криптографии, устойчивой к квантовым расчётам.

Как CMSS, так и GMSS имеют расширенную устойчивость подписи в сочетании с разумным временем проверки и разумной длиной подписи. GMSS предлагает схему с 280 подписями, зато имеет более низкую производительность в сравнении с CMSS. Задача решается разбиванием на отдельные деревья Мёркле с 2ⁿ листьев. Подпись из корня дерева используется для подписи открытого ключа, а ключ используется для создания по тому же принципу следующих деревьев.

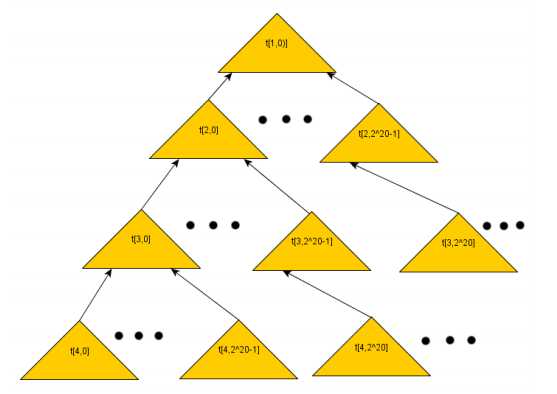Мне кажется, что любая их вышеприведенных схем в состоянии заменить ECDSA в мире, где уже есть полностью функциональный квантовый компьютер. Но почему бы не пойти дальше — мы можем реализовать это прямо сейчас и не ждать, пока АНБ приготовит нам сюрприз?

Будут ли данные схемы практичными в использовании? Давайте сделаем небольшое сравнение. Взглянем на время (t) и требования к памяти (m) для каждого алгоритма. CMSS имеет варианты 2²⁰, 2³⁰, и 2⁴⁰ , а вот GMSS может обеспечить длину подписи в 2⁴⁰ и 2⁸⁰.

Я бы предложил 2⁴⁰ и даже 2³⁰, этого будет вполне достаточно для Биткойн. Просто не могу представить кого -либо, кому понадобится совершать миллиарды и даже триллионы транзакций с одного биткойн-адреса. Также GMSS можно оптимизировать для ускорения времени верификации, правда, это на 25% увеличит размер подписи.

	mPrivKey	mPubKey	mSig	tKeygen	tSign	tVerify
ECDSA	32 байт	64 байт	71-73 байт	9.6 миллисекунд	100 миллисекунд	8.53 миллисекунд
CMSS20	1900 байт	46 байт	2128 байт	4.1 секунд	12.5 миллисекунд	2.0 миллисекунд
CMSS30	2788 байт	46 байт	2328 байт	2 минут	17.0 миллисекунд	2.0 миллисекунд
CMSS40	3668 байт	46 байт	2528 байт	62.3 минут	21.7 миллисекунд	2.0 миллисекунд
GMSS40	1640 байт	20 байт	1860 байт	723 минут	26.0 миллисекунд	19.6 миллисекунд
GMSS40′	1680 байт	20 байт	2340 байт	390 минут	10.7 миллисекунд	10.7 миллисекунд

Таким образом, мы видим из таблицы, что CMSS и GMSS обеспечивают лучшую производительность, чем ECDSA по таким параметрам как размер публичного ключа и время подписи. Тем не менее, те критичные для нас переменные, которые влияют на масштабируемость системы и размер подписи, не работают так хорошо, как нам хотелось бы. Время проверки у CMSS заметно лучше, чем у ECDSA. Похожие показатели времени проверки и оптимизированного варианта GMSS. Это реально может улучшить масштабируемость. А вот размер подписи у обеих определённо вызывает вопросы. Рассмотрим некоторые очень грубые оценки: в то время как размер транзакции сейчас — около 500 байт, CMSS или GMSS будет занимать около 4000 байт. Это означает, что для нас все новые транзакции блокчейна увеличатся на 700%. Блокчейн на сегодняшний день и так уже занимает 12.7 гигабайт.

Выдержит ли Биткойн такое большое счастье?

Если бы Биткойн использовал эти схемы с самого начала, его база прямо сейчас весила бы аж 100 гигабайт. При этом размер подписи и размер ключа примерно одинаковы у всех квантово-устойчивых схем, так что нам не удастся много выиграть, прибегнув к альтернативам алгоритмам хэширования.

Прошу заметить также, насколько велико при использовании GMSS время генерации кошельков. Полностью загрузите компьютер на целых 24 часа и вам удастся генерировать только 3 биткойн адреса. И это в случае использования оптимизированного варианта алгоритма, с увеличенными подписями!

Однако в этом есть и положительная сторона — подобного рода схема будет крайне устойчива к bruteforce-атакам (подбору ключей). Думаю, ускорить эти операции нам сможет помочь специальное ASIC-оборудование. А вот у CMSS показатели генерации кошельков не настолько уж плохи.

Так что, другими словами, Биткойн не может начать прямо сейчас использовать одну из этих схем цифровой подписи, если мы не хотим серьезно проиграть в производительности и масштабируемости системы. Потребуется дополнительная работа по оптимизации этих схем специально по объему цифровой подписи. Впрочем, возможно, что ко времени появления действительно полноценно работающих квантовых компьютеров закон Мура ещё во много раз удешевит стоимость хранения и обработки компьютерной информации, и пугающие нас сотни гигабайтов блокчейна будут помещаться на спичечной головке. Благодаря этому CMSS, GMSS и другие типы криптографии, устойчивой против квантового компьютера, удастся легко внедрить в  Биткойн. Ну а до тех пор —  нам не стоит слишком уж беспокоиться о действиях АНБ.

Источник: bitcoinnotbombs.com Автор: Chris

Поделиться ссылкой:

Related

bitnovosti.com

Квантовый компьютер как потенциальная угроза блокчейн

Биткоин использует две криптографические функции — SHA-256 для хеширования и ECDSA для общедоступных и закрытых ключей. Квантовый компьютер в основном представляет угрозу как объект, атакующий системы государственных сетей или секретные ключи и пароли. Внутри системы биткоин и других криптовалют открытые или закрытые ключи отображаются лишь во время транзакции.

Это означает, что биткоин находится в опасности от момента создания операции и до момента добавления её в цепочку.

Попытка взлома потребует крайне быстрого квантового компьютера, но он нескоро появится.

Квантовый компьютер: исходные вероятности

Пока рано беспокоиться, ведь программное обеспечение майнеров настроено на сохранение предстоящих блоков в течение закрытого периода времени: один блок каждые 10 минут для биткоинов и один блок в 2 минуты для некоторых версий.

Сейчас, с криптографическим алгоритмом SHA-256 в самом ядре конструкции блокчейна шансы угадывания правильной комбинации закрытых ключей оцениваются как один из 115 квадриллионов ещё и в степени.

То есть единица и 77 нулей за ней!

Согласитесь, это невероятно большое число, где количество комбинаций с частными ключами больше, чем существует песчинок на нашей планете. Поэтому шанс подобрать ключ без квантового компьютера к криптовалютному кошельку стремится к нулю.

В настоящее время для взлома потребуется около 0,65 миллиарда миллиардов лет. С квантовычислениями это резко изменится. Но насколько велик реальный риск?

Квантовый компьютер: потенциал

Скоростные компьютеры производят вычислительные процессы, основанные на квантовых свойствах, включая суперпозиции и запутанность. В будущем от этих машин ждут высокую производительность. Вначале рост составит несколько порядков. Затем новый уровень производительности обеспечит прорыв в смежных областях:

• системах искусственного интеллекта;
• симуляторов всевозможных процессов;
• прогнозирования вероятностей.

Квантовый компьютер обладает невероятной мощностью. Учитывая потенциальную силу, он может стать очень опасен и изменить мнение о надёжности сети блокчейн.

Шанс угрозы операциям блокчейн

Такое предположение как-то было выдвинуто на конференции, проходящей в Сиднее и посвящённой блокчейну. На техническом брифинге было высказано предположение, что с помощью квантового компьютера можно взломать один из 14 возможных биткоинов. Это примерно шанс в 7%. Со взломом протокола — цена цифровых валют резко упадёт — до тех пор, пока на слабое место не будет установлена защита, а доверие не начнёт возвращаться практически с нуля.

Учитывая, что Сатоши Накамото зарезервировал 1 миллион биткоинов, которые остаются нетронутыми, а сам протокол доказывает долговечность и безопасность с 2009 года, вероятно, средства будут направлены на дальнейшее совершенствование протокола.

1. Это поможет протоколу преодолеть потенциальный риск взлома, связанный с квантовыми компьютерами и вычислениями на новых скоростях.
2. Несомненно, в мировом масштабе найдутся команды программистов, рассматривающие разработку защиты от квантового компьютера, как выгодный вариант.
3. Наверняка есть и люди, убеждённые в перспективе блокчейн. Они также будут стремиться усовершенствовать базовый протокол.

Вероятно, игра «кошки-мышки» с квантовым компьютером будет продолжаться долгое время — до запуска новой машины и после. Не будем забывать о том, что открывающиеся возможности с удовольствием используют и команды криптосистем.

А как вы оцениваете надежность блокчейн с приходом квантовых машин? Напишите об этом в комментариях к статье.

Хотите больше новостей? Смотрите здесь и в Telegram. Следите за нами в соц. сетях: Twitter, Youtube, Google+, Instagram, Facebook, VK, OK. Подписывайтесь. Понравилась статья поделитесь с друзьями, на форумах, в соц. сетях — Вам не сложно 🙂 и Вы очень поможете нам развивать проект быстрее.

mining-bitcoin.ru

Квантовый компьютер может убить майнинг?

Специалист по квантовым компьютерам из Google считает угрозу майнингу нереальной

Угроза квантовых вычислений состоит в возможности дискредитировать шифрование и цифровые подписи RSA

Недавно руководитель лаборатории квантовых вычислений Джон Мартинес из компании Google отверг идею о том, что квантовые вычисления могут представлять прямую угрозу блокчейн системам и криптовалютам в ближайшем будущем. Выступая в Калифорнийском университете Санта-Барбара в рамках мероприятия Crypto 2017, Мартинес сообщил, что по его мнению, процесс создания квантовых компьютеров продлится не менее десятилетия. А практическая реализация эффективных квантовых вычислений займет еще больше времени. Он также заявил, что создание квантовых устройств «действительно проблематично и намного сложнее, чем создание классического компьютера».

Предполагаемая угроза от квантовых вычислений, заключается в том, что быстродействующие квантовые компьютеры, теоретически могут создать проблемы процессам шифрования RSA и цифровым подписям. «Это означает, что сверхскоростные вычисления позволили бы подделывать контракты и красть монеты», — заявил Бернардо Дэвид, эксперт по криптографии из Токийского технологического института. Мартин Томлинсон профессор Исследовательского центра безопасности, коммуникаций и сетевых технологий в Плимутском университете, в 2016 году, в своем интервью MSN, высказал гипотетическую угрозу, которую квантовые вычисления могут представлять для биткойна. Он выразил свою мысль следующим образом:

Если у вас есть квантовый компьютер, вы сможете просто вычислить закрытый ключ из открытого ключа … это займет минуту или две

А изучив все секретные ключи с помощью сверхскоростных вычислений на квантовом компьютере, вы сможете получить доступ ко всем доступном адресам сети биткойн.

Многие разработчики криптовалюты активно изучают угрозы, исходящие от будущих квантовых компьютеров

Опровергая угрозу, Мартинес указал на нестабильность квантовых бит (кубитов) — которые являются аналогами бит в классических вычислениях. Мартинес описывает кубиты как трехмерную версию битов, которые вместо строгих двух состояний 1 или 0 (как в случае с битами), могут одновременно представлять оба значения в динамическом массиве «суперпозиций». Таким образом, Мартинес утверждает, что популярное восприятие того, что конкурирующие исследовательские лаборатории квантовых вычислений участвуют в технологической гонке с целью генерации большего количества кубитов, является неточным, потому что не менее важное значение имеет цель уменьшения количества генерируемых при этом ошибок.

Несмотря на отдаленную гипотетическую перспективу угрозы, создаваемой квантовыми вычислениями, многие разработчики криптовалют активно стремятся заранее решить возможные в будущем проблемы. Так например, QRL или Quantum Resistant Ledger — это альткоин, который был разработан с возможностью уклоняться от квантовых вычислений и вооружен криптовалютной утилитой защиты. РКЦ России также заявил о своем намерении расширить исследования в области защиты от квантовых вычислений в системах блокчейн. Эти факты указывают на то, что криптовалютное сообщество серьезно воспринимает потенциальную угрозу, задолго до того, как квантовые вычисления станут реальностью.

Считаете ли вы, что квантовые вычисления представляют угрозу для блокчейн технологий и криптовалют? Или вы думаете, что разработчики найдут способы уклоняться от будущих угроз, исходящих от квантовых компьютеров? Поделитесь пожалуйста своими мыслями в разделе комментариев ниже!

crypinfo.ru

АНБ, квантовый компьютер и Биткоин

На днях благодаря очередному рассекреченному Эдвардом Сноуденом документу стало известно, что АНБ работает над созданием квантового компьютера.| Газета Washington Post осветила эту историю с довольно сенсационным заголовком: «АНБ стремится построить квантовый компьютер, способный взламывать большинство типов шифрования».

Естественно, это вызвало большое беспокойство среди новых поклонников Биткоин на Реддите и в Фейсбуке. На самом деле там не так уж много оказалось раскрыто, чего люди не знали или не ожидали. Общеизвестно, что АНБ и ранее спонсировало проекты создания квантовых компьютеров. Сам факт того, что внутри Агентства проект называется «Проникновение в труднодоступные цели» (Penetrating Hard Targets), новый, но не неожиданный. Мы узнали, что проект имеет бюджет в 79,7$ млн, но если честно, это не так уж много и, как заметила газета, документы не раскрывают, насколько далеко АНБ продвинулось в своих исследованиях. «Кажется маловероятным, чтобы АНБ существенно опережало в этом деле весь остальной мир, и никто об этом ничего не знал», — констатировали в Вашигтон Пост.

Тем не менее похоже, что сейчас самое подходящее время обсудить последствия внедрения квантовых вычислений в преломлении к будущему Биткоин.

Давайте начнем с маленького примера для тех, кто не знаком с квантовыми вычислениями. Современные компьютеры кодируют информацию в битах — бинарных числах 0 или 1. Эти биты обычно хранятся на жестком диске вашего компьютера. Их запись происходит путем изменения полярности намагниченности крошечных участков магнитного диска. Также биты хранятся в оперативной памяти или во флеш-памяти, где они представляют собой два различных уровня заряда в конденсаторе. Строки битов могут быть объединены для получения данных, которые могут быть прочитаны человеком. Например, строка 01000001 представляет собой букву «А» в расширенной таблице ASCII. Любые расчеты с битами выполняются последовательно, один за другим.

Фотонно-квантовые компьютеры используют различные состояния квантовых частиц, представляющих собой квантовые биты, сокращенно кубиты. Например, фотон, вращающийся в вертикальной плоскости, может быть 1, а в горизонтальной плоскости — 0. Наряду с этим фотоны могут существовать в довольно странном состоянии, называемом суперпозицией. То есть наряду с тем, что они могут вращаться в вертикальной, горизонтальной и диагональных плоскостях по отдельности, они также могут вращаться во всех этих направлениях одновременно. Даже не спрашивайте, как это возможно, это магия мира квантовой механики.

С практической точки зрения это означает, что в один момент времени обычный компьютер выполняет всего одно вычисление, в то время как квантовый может совершать миллионы калькуляций, повышая таким образом компьютерную производительность в миллионы раз.

Теперь когда журналисты пишут нечто вроде: «В металлических ящиках размером с комнату, защищенных от электромагнитных утечек, АНБ строит компьютер, который сможет взломать почти любой тип шифрования, используемый для защиты банковских, медицинских и правительственных данных по всему миру», — это, естественно, заставляет людей думать, что той криптографии, какой мы ее знаем сегодня, пришел конец. Но это не наш случай.

Давайте рассмотрим тот тип атаки, который приходит на ум большинству людей, когда они слышат о квантовых компьютерах — брутфорс. Это когда вы последовательно перебираете все ключи, пока не найдете нужный. Обладая достаточным количеством времени, вы можете подобрать любой ключ. Проблема в том, что для взлома достаточно длинного ключа шифрования обычному компьютеру потребуются миллиарды, а то и триллионы лет. Но, конечно, квантовые компьютеры могут с этим справиться, верно? Цитата из книги Брюса Шнейера «Прикладная криптография», написанной в 1996 году:

Один из выводов из второго закона термодинамики таков: для представления информации нужно определенное количество энергии. Для записи одного бита путем смены состояния системы требуется энергии не меньше, чем kT, где Т есть абсолютная температура системы, а k — постоянная Больцмана (не расходитесь, урок физики почти закончился).

Учитывая, что k = 1.38×10^(-16) эрг/° Кельвина, а температура вселенной равна 3.2° Кельвина, идеальный компьютер, работающий при температуре 3.2°K будет потреблять 4.4×10^(-16) эрг каждый раз при смене бита. Для того, чтобы компьютер работал при температуре холоднее, чем космическая радиация, потребуется дополнительная энергия для запуска теплового насоса.

Далее, годовой объем энергии, выделяемой нашим Солнцем, примерно составляет 1.21×10^41 эрг. Этого достаточно для 2.7×10^56 изменений битов в нашем идеальном компьютере, то есть для того, чтобы прокрутить 187-разрядный счетчик от нуля до максимума. Если бы мы построили сферу Дайсона вокруг Солнца и удерживали бы всю его энергию без потерь в течение 32 лет, наш компьютер досчитал бы до 2^192. Правда, при этом на выполнение каких-либо более полезных операций энергии бы уже не осталось.

Но это только одна звезда, причем далеко не самая массивная. Типичная сверхновая излучает порядка 10^51 эрг. В форме нейтрино излучение в сотню раз больше, но мы их не трогаем, пусть себе летят. Если бы вся эта энергия могла бы быть собрана воедино в неистовой вычислительной оргии, мы бы смогли прокрутить от начала до конца 219-битный счетчик.

Эти цифры не имеют ничего общего с технологией устройств, просто это тот максимум, который позволяет достичь термодинамика. Кроме того, они означают, что брутфорс, направленный на 256-битные ключи, невозможен, пока компьютеры не построены из чего-то другого, чем материя, и не занимают нечто иное, чем пространство.

Повторим еще раз. Даже если вы соберете всю энергию от сверхновой воедино и направите ее в идеальный компьютер, вы все равно не сможете взломать простым перебором обычный ключ шифрования. Следовательно, если вы собираетесь взламывать коммерческие коды, вы должны атаковать математику, лежащую в основе алгоритма шифрования.

Сегодня большинство алгоритмов шифрования с открытым ключом опираются либо на трудности целочисленной факторизации (RSA), либо на задачи дискретных логарифмов (DSA/El Gamal и криптография эллиптических кривых). В 1994 году математик Питер Шор (Peter Shor) продемонстрировал эффективный квантовый алгоритм для факторинга и вычисления дискретных логарифмов, который мог бы взламывать шифры с открытыми ключами, если бы использовался на квантовом компьютере. Правда, он может взломать далеко не все типы кодирования. Традиционная криптография с симметричным ключом и криптографические хеш-функции все равно будут лежать далеко за пределами поля зрения квантовых алгоритмов.

Влияние на Биткоин

В Биткоин используется несколько алгоритмов шифрования: алгоритм цифровой подписи эллиптических кривых (ECDSA) для подписи транзакций и хеш-функции SHA-256 и RIPEMD160. Если АНБ сможет разработать квантовый компьютер, пригодный для взлома шифров, то ему удастся преодолеть ECDSA, однако SHA-256 и RIPEMD160 устоят.

Хорошая новость в том, что в случае признаков взлома ECDSA его достаточно легко заменить на другой тип шифрования. Было бы гораздо хуже, если бы в опасности оказался SHA-256. Если вы не знакомы с механикой Биткоин, напомним, что SHA-256 используется при майнинге. На данный момент миллиарды долларов были потрачены на компьютерные чипы, которые не выполняют ничего другого, кроме вычислений SHA-256. В случае уязвимости алгоритма SHA-256 всё это железо превратится в дорогое пресс-папье. Если бы такое произошло внезапно (в отличие от плавного перехода на другую хеш-функцию), это стало бы катастрофой. Безопасность сети Биткоин опирается на тот факт, что контролировать 51% вычислительных мощностей сети слишком сложно и дорого для злоумышленника. Внезапный переход на другую хеш-функцию создаст значительную угрозу безопасности и, скорее всего, вызовет обвал цен на биткоины. Но как уже говорилось, майнеры могут спать спокойно: квантовые компьютеры алгоритму SHA-256 не страшны. Хотя это не означает, что никто не сможет найти брешь для атаки в будущем.

Вернемся к ECDSA. Этот алгоритм генерирует пару ключей, один из которых открытый, а другой — закрытый. В Биткоин вы храните приватный ключ у себя и используете его для подписи транзакций, доказывая сети, что у вас есть биткоины, связанные с определенным адресом. Сеть проверяет вашу подпись, используя соответствующий открытый ключ. Работающий квантовый компьютер позволит АНБ отделить закрытый ключ от открытого. Значит ли это, что АНБ сможет украсть биткоины у каждого? Не совсем так.

Дело в том, что в Биткоин ваш открытый ключ (изначально) не является открытым. Пока вы не делитесь адресом вашего кошелька с другими, чтобы они смогли прислать вам монетки, ваш адрес — это только хеш-функция открытого ключа, а не сам ключ. Другими словами, хеш-функция — это односторонняя криптографическая функция, которая берет данные на входе и возвращает их в зашифрованном виде на выходе. Обратный процесс невозможен. Под односторонней функцией понимается то, что после операции хеширования вы уже не сможете отделить входные данные от того, что получилось на выходе. Так же, как если бы вы что-то зашифровали, а потом потеряли ключ. Для демонстрации давайте посчитаем RIPEMD160 хеш-функцию фразы «Hello World».

Hello World ==> a830d7beb04eb7549ce990fb7dc962e499a27230

Адрес кошелька Биткоин высчитывается из вашего открытого ключа путем запуска нескольких хеш-функций подряд вот таким образом:

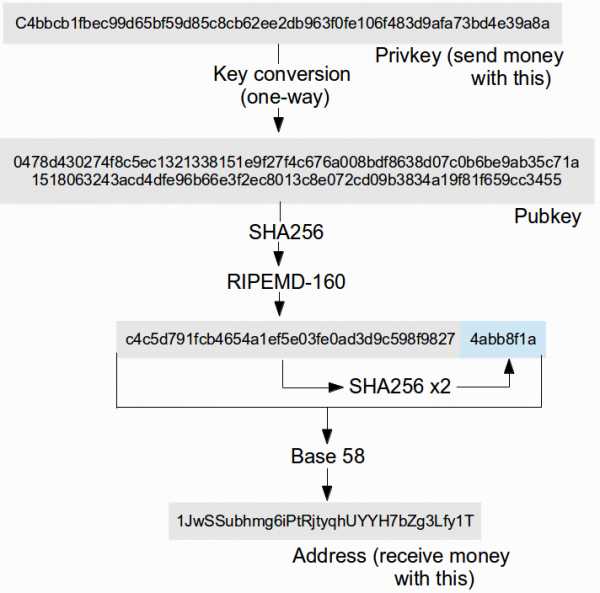
Все написанное здесь — замысловатый способ показать вам, что злоумышленник с квантовым компьютером, даже отделив закрытый ключ от открытого, не сможет получить открытый ключ из адреса биткоин-кошелька, потому что он пропущен через несколько односторонних квантовоустойчивых хеш-функций.

Тем не менее для совершения транзакции вы должны транслировать в сеть свой открытый ключ — нет другого способа проверить вашу подпись. Это означает, что в страхе перед квантовым компьютером АНБ все Биткоин-адреса должны являться одноразовыми. Всякий раз,  проводя транзакцию, вы должны переслать все лишние биткоины на вновь созданный адрес. Если вы не удалите весь баланс с вашего адреса, АНБ сможет украсть остаток. Это неудобно, но даст разработчикам достаточно времени, чтобы поменять ECDSA на квантовоустойчивую схему цифровой подписи.

Постквантовые цифровые подписи

Этот раздел будет немного техническим, но не особо сложным даже для начинающих. Существует несколько типов постквантовых систем шифрования с открытыми ключами: на основе теории решеток, кодов исправления ошибок, многомерных квадратичных схем и хеш-функций. Как уже упоминалось, криптографические хеш-функции предполагаются квантовоустойчивыми. При этом условии возможноа замена схемы цифровой подписи для ECDSA с использованием только хеш-функций. Давайте посмотрим на эти хеш-системы, так как они просты для понимания и основаны на уже широко использующихся хеш-функциях.

Схема одноразовой подписи Лэмпорта (LOTSS)

Для начала, чтобы обеспечить адекватную защиту, мы должны использовать хеш-функцию с как минимум 160-битным выходом. RIPEMD160 или SHA-1 должны подойти для этого. Чтобы сгенерировать пару открытый/закрытый ключ, мы начнем с генерации 160 пар случайных чисел. Этот набор случайных чисел будет закрытым ключом.

Пара №	Открытый ключ
1	e9e515b332cf1ce01299497e9e94b7df353ff022 ce56dcfdb7038e6ab0b37c383dbfda8cb45d60ea
2	811f71c5cf7639a40df7b9b187bf768016791cf8 1094b13455a133d2d11898cfa30916e12be3e0ab
…
159	bc6a1eb98148850dd2b32ae632005f5472c06a70 c10f4ac3d645d891d9b5dc0fa0b7294ad14ac3df
160	585801c9da7ce0d562f375338b456ba9f10be3f6 3c3363ed7273f1ef9c1aed3fc5a7433002b668f8

Для генерации открытого ключа мы возьмем хеш-функцию RIPEMD160 каждого из 320 чисел.

Пара №	Закрытый ключ	Открытый ключ
1	e9e515b332cf1ce01299 ce56dcfdb7038e6ab0b3	d7c3e127380fbbbe37b9 4ddf29fb200aa0fd90b1
2	811f71c5cf7639a40df7 1094b13455a133d2d118	f84a8e5a0dce682e48c5 4a88310f694329b9ab97
…
159	bc6a1eb98148850dd2b3 c10f4ac3d645d891d9b5	7d5c0e19c4dc9077be6c ffbbe97612e581f073b6
160	585801c9da7ce0d562f3 3c3363ed7273f1ef9c1a	38ed36c30ee72c95c598 a546f885e8210c61767d

Теперь, чтобы подписать сообщение подписью Лэмпорта, мы сперва сделаем каталог сообщений путем их хеширования с помощью RIPEMD160 (в Биткоине мы бы хешировали транзакцию), а потом сконвертируем то, что вышло, в бинарный вид. Попробуем в качестве примера опять использовать фразу «Hello World»:

Hello World ==> a830d7beb04eb7549ce990fb7dc962e499a27230 ==> 101010000011000011010111101111101011000001001110101101110101
01001001110011101001100100001111101101111101110010010110
00101110010010011001101000100111001000110000

Далее мы сопоставим каждую двоичную цифру с каждой парой нашего закрытого ключа. Если бит 0 — мы добавляем первое число пары к нашей подписи, если 1 — второе число.

Пара №	Каталог	Закрытый ключ	Подпись
1	1	e9e515b332cf1ce01299 ce56dcfdb7038e6ab0b3	ce56dcfdb7038e6ab0b3
2	0	811f71c5cf7639a40df7 1094b13455a133d2d118	811f71c5cf7639a40df7
…
159	0	bc6a1eb98148850dd2b3 c10f4ac3d645d891d9b5	bc6a1eb98148850dd2b3
160	0	585801c9da7ce0d562f3 3c3363ed7273f1ef9c1a	585801c9da7ce0d562f3

Наконец, чтобы проверить, является ли подпись действительной, мы опять сперва создаем каталог сообщений, используя описанный выше процесс, затем хешируем каждое из 160 чисел в подписи с помощью RIPEMD160 и, наконец, проверяем, совпадают ли эти хеши с хешами открытого ключа, представленными в каталоге сообщений.

Пара №	Хеш подписи	Каталог	Открытый ключ
1	4ddf29fb200aa0fd90b1	1	d7c3e127380fbbbe37b9 4ddf29fb200aa0fd90b1
2	f84a8e5a0dce682e48c5	0	f84a8e5a0dce682e48c5 4a88310f694329b9ab97
…
159	7d5c0e19c4dc9077be6c	0	7d5c0e19c4dc9077be6c ffbbe97612e581f073b6
160	38ed36c30ee72c95c598	0	38ed36c30ee72c95c598 a546f885e8210c61767d

Вот и получили, что хотели — квантовоустойчивую схему цифровой подписи, используя только хеш-функции. Только лицо, владеющее всеми 320 числами в закрытом ключе, сможет сгенерировать подпись, которая хеширует открытый ключ при сравнении с каталогом. Однако хотя эта схема фактически рабочая, она не без проблем. Во-первых, как следует из названия, подпись по методу LOTSS можно использовать только один раз. Причина в том, что вы в каждой подписи выкладываете по сути половину своего закрытого ключа. При таком раскладе, если подписывать несколько сообщений, то закрытый ключ будет полностью скомпрометирован. Применительно к Биткоин такую схему также можно было бы использовать только один раз.

Еще одна проблема в том, что размеры ключей и сигнатур получились абсурдно большими. Закрытый и открытый ключ суммарно весят 6400 байтов (сравните с 32 и 64 байтами для ключей с использованием алгоритма ECDSA). Аналогично, полученная нами подпись занимает 3200 байтов (71-73 байта при ECDSA). Биткоин уже имеет проблемы с масштабированием, и такое увеличение размеров ключей и подписей только усугубит их.

Закрытый ключ Лэмпорта может быть сильно уменьшен в размерах путем генерации случайных чисел из одного случайного источника (seed). Чтобы сделать это, нужно просто взять RIPEMD160 (seed + n), где n начинается с 1 и при каждой итерации увеличивается на единицу, пока не достигнет 320. К сожалению, размер закрытого ключа — не такая большая проблема, как размер открытого ключа и подписи. Есть еще одна схема одноразовой подписи, называемая подписью Винтернитца, в которой размера ключа может быть уменьшен, но это происходит за счет хеш-операций. К счастью, мы еще не закончили.

Схема подписи Меркля (MSS)

Схема подписи Меркля совмещает схему одноразовых подписей (либо Лэмпорта, либо Винтернитца) с деревом Меркля, также называемым деревом хешей. Такой подход позволяет подписывать одним открытым ключом много сообщений, не беспокоясь о безопасности. Давайте посмотрим, как это работает.

Мы начнем с создания ряда пар ключей Лэмпорта. Их количество будет равно количеству подписей, которые мы хотим получить из одного открытого ключа. В качестве примера возьмем, например, восемь. Затем вычислим дерево Меркля, используя каждый из восьми открытых ключей Лэмпорта. Для этого открытые ключи разбиваются на пары, хешируются, затем полученные хеши объединяются путем конкатенации и итоговые результаты снова хешируются. Этот процесс, похожий на замешивание теста, повторяется, пока не выйдет единый ком.

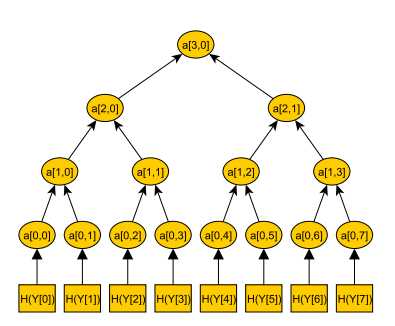
Хеш на самой вершине дерева (корень Меркля) — это открытый ключ Меркля. Такой способ значительно уменьшает размер открытого ключа с 6400 (в случае подписи Лэмпорта) до 20 байтов, то есть до длины одного RIPEMD160 хэша. Для расчета подписи надо выбрать одну пару ключей Лэмпорта и подписать сообщение точно так же, как мы делали это выше. Но в этот раз подпись будет состоять из подписи Лэмпорта и каждого листа дерева Меркля, ведущего от открытого ключа к корню.

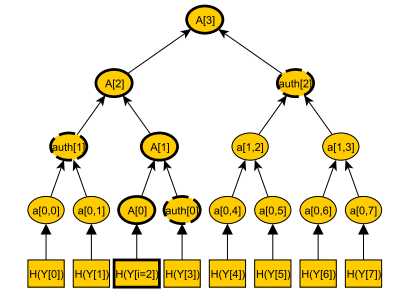
На диаграмме выше подпись будет такой:

sig′||H(Y[i=2])||A[0]||auth[0]||A[1]||auth[1]||A[2]||auth[2]||A[3]

Для верификации подписи Меркля достаточно проверить подпись Лэмпорта, а затем убедиться, что листья хешируются в открытый ключ Меркля. Если все так, подпись действительна.

Итак, какие есть преимущества MSS над LOTSS? Во-первых, открытый и закрытый ключи весят 20 байтов вместо 6400. Во-вторых, к одному открытому ключу можно сделать множество подписей, правда, здесь есть немалая проблема. Чем больше сообщений вы хотите подписать своим открытым ключом, тем больше должно быть дерево Меркля. Чем больше дерево, тем больше подпись. В итоге подпись может стать такой большой, что ее использование окажется непрактичным, особенно в случае с Биткоин. Это приводит нас к последней постквантовой схеме подписи, которую мы сейчас и обсудим.

CMSS и GMSS

Схема подписи Меркля известна уже более 30 лет, и несмотря на развитие криптоанализа ее ценность для шифрования не была опровергнута. Тем не менее в последние пять лет ее неоднократно пытались улучшить, что привело к интересным результатам. Так, появились Улучшенная (CMSS) и Обобщенная (GMSS) схемы подписи Меркля. Оба стоящих за этими схемами криптографа являются авторами книг по постквантовой криптографии.

Обе схемы предлагают существенное увеличение количества подписей на один открытый ключ с сохранением разумной длины подписи и временем ее верификации. GMSS, в частности, предлагает практически неограниченное количество подписей — 2^80, но при этом показывает несколько меньшую производительность по сравнению с CMSS. Обе схемы решают задачу, разбивая систему на отдельные деревья Меркля с 2^n листьями. Подписью корневого дерева подписывается открытый ключ дерева ниже, которое в свою очередь также является подписью к дереву под ним, и так далее.

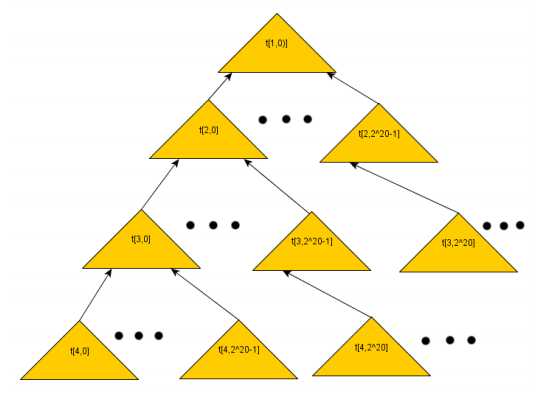
Таким образом, весьма вероятно, что какая-то из этих схем подписи станет серьезным кандидатом на замену ECDSA в Биткоин в постквантовом мире. Но почему бы нам самим не пойти дальше и попробовать реализовать его сейчас, вместо того, чтобы ждать, пока нас всех удивит АНБ? Давайте сделаем небольшое сравнение и посмотрим на скорость операции и размеры подписей для каждой схемы. Варианты CMSS имеют емкость хранения подписей 2^20, 2^30 и 2^40, в то время как для GMSS она составляет 2^40 и 2^80. Скорее всего, и 2^30 подписей было бы достаточно для Биткоин, потому что трудно себе представить кого-то, кто может сделать больше миллиарда или триллиона транзакций с одного кошелька. Еще схема GMSS может быть оптимизирована для более быстрой верификации, правда, ценой увеличения размера подписи на 25%.

	Размер закрытого ключа	Размер открытого ключа	Размер подписи	Время генерации	Время создания подписи	Время верификации
ECDSA	32 байта	64 байта	71-73 байта	9.6 мс	100 мс	8.53 мс
CMSS20	1900 байт	46 байт	2128 байт	4.1 сек	12.5 мс	2.0 мс
CMSS30	2788 байт	46 байт	2328 байт	2 мин	17.0 мс	2.0 мс
CMSS40	3668 байт	46 байт	2528 байт	62.3 мин	21.7 мс	2.0 мс
GMSS40	1640 байт	20 байт	1860 байт	723 мин	26.0 мс	19.6 мс
GMSS40′	1680 байт	20 байт	2340 байт	390 мин	10.7 мс	10.7 мс

Из таблицы видно, что CMSS и GMSS фактически работают лучше, чем ECDSA, в отношении размера открытого ключа и времени подтверждения подписи. Однако в критичных вещах, которые влияют на масштабируемость и размер подписи, они хуже. Время верификации для CMSS на самом деле лучше чем у ECDSA, что должно улучшить масштабируемость, а оптимизированный вариант GMSS также находится весьма близко к желаемым значениям. Тем не менее размер подписи для обеих схем остается существенной проблемой. Давайте проведем грубую оценку.

Сейчас размер транзакции — около 500 байтов. Оба варианта — и CMSS, и GMSS — увеличат транзакцию до 4 килобайт. Это означает увеличение размера блока в цепочке на 700%. Вся цепочка блоков на сегодняшний день превышает 13 гигабайт. Если бы Биткоин использовал эти схемы подписей с самого начала, то уже сейчас цепочка «весила» бы более 100 гигабайт. Подпись и размер ключа являются проблемой не только для описанных схем, остальные находятся в той же ловушке.

Стоит обратить внимание также и на сумасшедшее время генерации ключа у GMSS. Если вы оставите компьютер включенным на сутки, вы сможете сгенерировать всего три кошелька, и это используя оптимизированный вариант с увеличенными размерами подписей. Хотя подозреваю, что оборудование ASIC значительно ускорило бы время генерации кошельков. У CMSS с этим не все так плохо.

Другими словами, Биткоин не может сейчас перенять ни одну из этих схем подписи, если он хочет продолжать масштабироваться. Однако с течением времени квантовые компьютеры становятся все более жизнеспособными, а закон Мура скорее всего доведет стоимость хранения и вычислительную мощность до той точки, когда CMSS, GMSS или какой-нибудь другой тип постквантовой подписи сможет быть внедрен в Биткоин. До тех пор давайте не забывать об АНБ и его проекте «Проникновение в труднодоступные цели».

 

Источник: BitcoinNotBombs

coinspot.io

Исследование: квантовый компьютер взломает блокчейн биткоина уже к 2027 году

Через десять лет вычислительные машины на квантовых принципах станут угрозой для лежащей в основе криптовалют технологии блокчейн. К такому выводу пришел международный коллектив исследователей в своей статье, препринт которой опубликован на сайте arXiv.org.

По утверждению авторов, большинство современных криптографических протоколов, обеспечивающих безопасность интернет-транзакций и финансовых операций, потенциально уязвимы для достаточно большого квантового компьютера. К сервисам, которым грозит взлом, они отнесли и криптовалюты, в частности, биткоины.

При этом исследователи выяснили, что майнинг биткоинов находится в относительной безопасности, так как в ближайшем будущем оборудование для добычи криптовалют по-прежнему будет намного мощнее квантовых компьютеров.

Более уязвимым оказался алгоритм создания цифровой подписи на основе эллиптических кривых, используемый в этой криптовалюте. В целом, по мнению авторов статьи, квантовые компьютеры создадут угрозу биткоину к 2027 году.

«Такая атака может быть эффективна, так как при совершении операций с биткоинами между трансляцией транзакции и ее обработкой с сохранением в блокчейне проходит около десяти минут. Через десять лет квантовые компьютеры за это время смогут вычислить приватный ключ на основе публичного, что позволит, например, перенаправить передаваемые средства на другой кошелек», — предупреждают ученые.

Добавим, что в своей работе исследователи рассмотрели различные схемы постквантового шифрования, устойчивого для взлома квантовым компьютером, и другие методы противодействия такому виду атак.

Напомним, в апреле анонимная группа «Большой биткоин-коллайдер» заявила, что может взламывать биткоин-кошельки, используя так называемую атаку методом грубой силы, направляя огромные количества вычислительных мощностей на подбор приватных ключей к индивидуальным кошелькам.

Подписывайтесь на новости ForkLog в Telegram: ForkLog — вся лента новостей, ForkLog Live — самые важные новости и опросы!

Нашли ошибку в тексте? Выделите ее и нажмите CTRL+ENTER

Подписаться на новости Forklog

forklog.com

Квантово-устойчивый блокчейн / Habr

В этой статье я расскажу о проблеме безопасности в технологии блокчейн в свете роста производительности квантовых компьютеров, разберу некоторые методы защиты от атак с применением квантового компьютера и о недавно появившемся проекте: Quantum-Resistant Ledger. Как заявляют разработчики, это будет первая в мире платформа, построенная на принципах постквантового шифрования и предназначенная для обеспечения защиты от «квантового удара» на случай быстрого развития этих технологий. Такому удару могут быть подвергнуты платформы, построенные с использованием классических принципов шифрования. Без фундаментальных изменений Bitcoin, Ethereum, Ardor и большинство подобных платформ в недалеком будущем могут оказаться в уязвимости.

Часть 1. Проблема безопасности

Уязвимость

Алгоритм защиты Биткойна и подобных систем построен по принципу асимметричного шифрования с открытым и закрытым ключом. Транзакция подписывается закрытым ключом, а ее истинность проверяется с помощью открытого ключа.

С использованием классических алгоритмов атаки практически невозможно найти закрытый ключ, зная открытый. Системы асимметричного шифрования, такие как RSA и подобные (DSA, DH и пр.), построены на том утверждении, что сложность разложения числа на простые множители растет экспоненциально от размера ключа. Однако, с использованием алгоритма Шора на квантовом компьютере становится возможным за полиномиальное время разложить число на простые множители и, таким образом, найти закрытый ключ, зная открытый.

В 2001 году компания IBM продемонстрировала эту возможность, разложив число 15 на два простых множителя 3 и 5. Для этих целей был использован квантовый компьютер, состоящий из 7 кубитов. С тех пор развитие технологий квантовых вычислений происходит все быстрее.

В 2016 году группа исследователей из Массачусетского технологического института совместно с институтом Иннсбрука выполняет ту же задачу по разложению числа 15, использовав всего 5 кубитов.

В июле 2017 российско-американскими физиками был создан программируемый 51 кубитный компьютер.

В конце октября 2017 Международная исследовательская группа из Сингапурского и Австралийского университетов пришла к выводу, что большинство криптографических протоколов, применяемых в блокчейне, уязвимо к атакам мощного квантового компьютера. В отчете группы приводятся 2 прогноза роста мощности квантового компьютера: оптимистичный и менее оптимистичный. Согласно первому, количество кубит квантового компьютера будет удваиваться каждые 10 месяцев. Менее оптимистичный прогноз говорит об удвоении количества кубит каждые 20 месяцев. На рисунке ниже представлены графики обоих прогнозов.

Наиболее уязвимым к атакам квантового компьютера признан алгоритм создания цифровой подписи на основе эллиптических кривых (ECDSA). Таким образом, говорится в отчете группы, Биткойн в его классическом виде может быть взломан уже к 2027 году.

Может, не все так плохо? Публичный ключ не хранится в открытом виде

В конце апреля 2017 года на сайте bitcoin.com выходит статья, призванная ответить на вопрос, стоит ли держателям Биткойна опасаться его взлома с помощью квантового компьютера. В ней говорится, что не смотря на то, что в блокчейне Биткойн применяется асимметричное шифрование, пользователям не стоит опасаться за сохранность своих монет. Открытый ключ не хранится в открытом виде. Так, адреса для передачи монет не являются открытыми ключами, а лишь результатом применения хеш-функции SHA-256. Функция хеширования выполняет одностороннее преобразование и поэтому является устойчивой к атакам квантового компьютера.

Публичный ключ становится известен во время транзакции

Утверждение, что публичный ключ не доступен в открытом виде, не совсем верное. Не вдаваясь в мелкие подробности, разберем на примере Биткойна (BTC), как происходит передача криптовалюты от одного человека к другому.

Пусть Алиса в своем кошельке на одном из Биткойн-адресов имеет 100 mBTC (1000 mBTC = 1 BTC). Она хочет перевести Бобу 1 mBTC. Для этого она указывает Биткойн-адрес Боба, комиссию за перевод и Биткойн-адрес в ее кошельке для получения сдачи. Пусть в качестве комиссии Алиса указала 1 mBTC. Таким образом, из 100 mBTC, имеющихся у Алисы 1 mBTC отправляется Бобу, 1 mBTC уходит в качестве комиссии сети Биткойн и 98 mBTC возвращается в кошелек Алисы.

Теперь разберем, что же происходит на уровне сети Биткойна. У Алисы и Боба есть кошельки, содержащие адреса для хранения монет. Один кошелек может содержать несколько Биткойн-адресов. Адреса генерируются при создании кошельков. Каждому адресу соответствует созданная по алгоритму ECDSA пара ключей: открытый и закрытый. При передаче монет создается транзакция, в которой передается информация о количестве передаваемых Алисой монет, Биткойн-адрес Боба, подпись, выполненная закрытым ключом Алисы, публичный ключ Алисы и некоторые другие данные. Далее транзакция в открытом (нешифрованном) виде отправляется в сеть. Узлы сети, прежде чем принять транзакцию к обработке, проверяют ее подпись используя открытый ключ. В случае достоверности подписи они добавляют информацию о транзакции в блок. Такая операция включения называется подтверждением.

Среднее время генерации блока в сети Биткойн составляет 10 минут. Сеть стремится поддерживать это время постоянным. Прежде чем использовать полученные средства, рекомендуется дождаться 6 подтверждений. Таким образом, Боб, соблюдая правила безопасности, сможет воспользоваться полученными средствами примерно через час после их перевода.

Одной из особенностей передачи монет в сети Биткойн является то, что не возможно передать только часть монет с одного адреса. Монеты всегда передаются всем объемом, находящимся на Биткойн-адресе кошелька, при этом отправителю возвращается сдача. Ее можно получить как на тот адрес, с которого монеты были отправлены, так и на любой другой. Поэтому Алиса должна указать адрес для сдачи. В ряде программного обеспечения, осуществляющего функционирование кошелька, адресом сдачи является адрес отправки.

Комиссия за транзакцию, строго говоря, не является обязательной, но ее отсутствие может надолго отложить выполнение транзакции. Справедливо и обратное утверждение: можно несколько ускорить прохождение транзакции, увеличив размер комиссии. На момент написания статьи (январь 2018) большинство ПО кошельков предлагает указать комиссию в размере 1 mBTC. Есть ряд ресурсов, например, этот, которые позволяют оценить время включения транзакции в блок в зависимости от размера комиссии.

Использование открытого ключа 1 раз

С точки зрения безопасности, лучше всего получать сдачу на новый адрес, открытый ключ которого будет неизвестен сети. В этом случае, пара ключей используется только 1 раз. Однако, согласно статистике по состоянию на декабрь 2017 года около 41,34% адресов используется повторно.

10 минут, чтобы совершить атаку

Тем не менее, вам рано или поздно потребуется воспользоваться средствами, лежащими на новом адресе. Публичный ключ передается в сеть в открытом виде. Пока не пришло подтверждение, средства все еще находятся у отправителя. Если злоумышленник получит открытый ключ во время проведения транзакции, у него будет около 10 минут, чтобы получить закрытый ключ с помощью квантового компьютера и попытаться провести свою транзакцию с того же адреса, задав повышенную комиссию.

Статические адреса более уязвимы

В таких системах как Ethereum, NXT, Ardor и др. открытый ключ становится также известным после первой транзакции. Ситуация усугубляется тем, что токены или смарт-контракты привязаны к статическим адресам, атака на которые может проводиться продолжительное время. Если атака будет успешной, то злоумышленник сможет разрушить всю основанную на этих адресах экономическую систему.

Часть 2. Пути решения

Чем обеспечить устойчивость к атакам квантового компьютера?

В настоящий момент существует несколько основных методов, обеспечивающих защиту от атак квантового компьютера:

• криптография на основе хешей;
• криптография на основе кода;
• криптография на основе матрицы;
• криптография, основанная на многомерных квадратичных системах;
• криптография на базе секретного ключа.

При наличии достаточно длинных ключей и соблюдении требований к безопасности данные методы защиты способны противостоять как классическим атакам, так и атакам с использованием квантового компьютера.

Наиболее изученным является использование цифровых подписей на основе хеш-функций.

Как уже было сказано ранее, хеш-функция выполняет одностороннее преобразование сообщения. Сообщение преобразуется в значение хеша фиксированной длины. Использование хеш-функции с одной стороны должно сделать бессмысленным перебор сообщений для получения аналогичного значения хеша. С другой стороны, алгоритм должен быть устойчив к коллизиям: когда 2-м разным сообщениям соответствует одно и то же значение хеш-функции.

Квантовый алгоритм Гровера может быть использован для попытки найти коллизию или выполнить предварительную атаку, чтобы найти исходное сообщение. Для этого потребуется операций. Таким образом, для поддержания 128-ми битной безопасности, необходима длина результирующего хеша не менее 256 бит. В качестве такой функции может быть выбрана SHA-256.

Подпись Лэмпорта

Одним из вариантов использования хеш-функции в цифровой подписи является подпись Лэмпорта. Она может быть построена на основе любой односторонней хеш-функции. Криптоустойчивость алгоритма основана на криптоустойчивости применяемых хеш-функций.Схема подписиДля сообщения длиной генерируются ключи. Сперва парами генерируются закрытые ключи длиной , затем, применяя хеш-функцию, из закрытых ключей формируются пары открытых ключей . Количество пар закрытых и открытых ключей равно количеству бит в исходном сообщении.
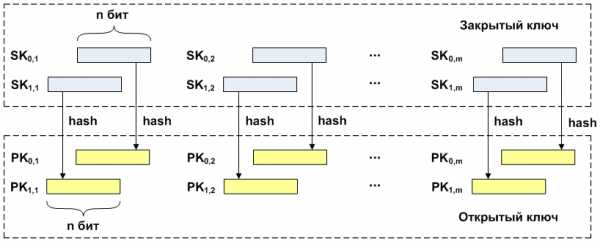
При выполнении подписи, побитово читается сообщение, и, в зависимости от значения текущего бита, выбирается один из закрытых ключей соответствующей пары. Выбранные закрытые ключи объединяются в подпись. Далее получившуюся подпись и пар открытых ключей отправляются адресату.

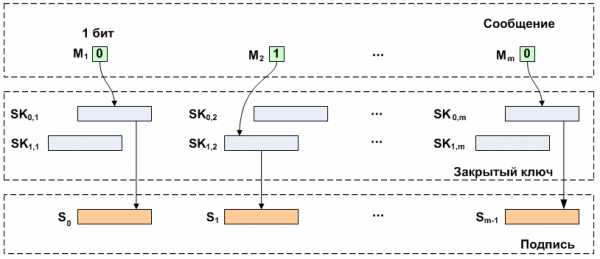
Проверка подписи похожа на процесс ее создания. Подпись разбивается на фрагменты длиной , которые затем преобразуются при помощи той же хеш-функции. Побитово читается сообщение и значением бита выбирается открытый ключ, который сравнивается с полученным значением хеша.

Как правило, перед применением подписи исходное сообщение хешируется для уменьшения его размера. Пусть в качестве хеш-функции выбрана SHA-256, тогда . При этом общая длина открытого (как и закрытого) ключа получается равной:

Длина подписи составляет:

Подпись Лэмпорта является одноразовой (остается безопасной только при однократном ее использовании), поскольку при ее выполнении и передаче становится известной половина закрытого ключа. Пусть длина сообщения равна 256 байт и длина хеша равна 256. До того, как Алиса опубликует подпись к сообщению, никто не знает 2 * 256 случайных чисел в секретном ключе. Таким образом, никто не может создать правильный набор из 256 чисел для подписи.

После того, как Алиса опубликует подпись, никто все еще не будет знать остальные 256 чисел, и, таким образом, не сможет создать подпись для сообщений, имеющих иной хеш.

Тот факт, что подпись Лэмпорта является одноразовой, в сочетании с внушительным суммарным объемом подписи и открытого ключа (24 КБ при длине сообщения в 256 байт и длиной хеша в 256 байт), делает ее использование в публичном блоке транзакций нецелесообразным.

Подпись Винтерница

Существуют и другие алгоритмы одноразовой цифровой подписи. В подписи Винтерница, в отличие от подписи Лэмпорта, исходное сообщение подписывается не побитово, а блочно. Одноразовая подпись Винтерница, как и Лэмпорта, может быть построена на основе любой стойкой криптографической функции.Схема подписи
Размеры открытого ключа и подписи, при тех же параметрах, что и в примере для подписи Лэмпорта, равны 1 КБ. В сумме это меньше, чем в подписи Лэмпорта (24 КБ). Однако, количество операций вычисления хеша при этом составляет 8160. Что, несомненно, очень много. К тому же, при проверке подписи выполняется в среднем половина от этого количества итераций. Это делает данный вариант подписи нецелесообразным для использования в блокчейне.

Существует несколько вариантов подписи Винтерница, в том числе с расширением подписи с целью повышения надежности и сокращения количества применений хеш-функции. Их описание выходит за рамки данной статьи. Те, кому интересно, могут посмотреть подробнее здесь. Применение подписи Винтерница на базе отечественной хеш-функции ГОСТ 34.11-12 можно посмотреть здесь.

Дерево Меркла (MSS)

Одноразовые подписи способны обеспечить удовлетворительную криптографическую безопасность, однако, именно их одноразовость может стать серьезной проблемой. Пусть необходимо передать сбережения с одного адреса на другой. При этом получается, что при использовании одноразовых подписей необходимо будет каждый раз переводить весь объем средств, и для проведения каждой транзакции нужен будет новый адрес. С каждой транзакцией нужно будет публиковать новый открытый ключ. Кроме того, сохранение в блокчейне новых транзакций постепенно будет требовать все больше времени на их поиск.

Для решения проблемы расширяют схему подписи за счет проведения нескольких подписываний на основе нескольких пар ключей для каждого адреса. Использование нескольких подписей выполняют на базе двоичного хеш-дерева — дерева Меркла.

Подробнее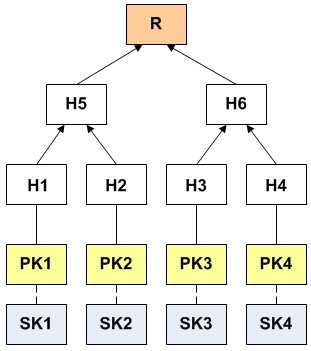

Вычисление дерева производится от листьев к корню. Каждый узловой лист дерева вычисляется как хеш от сгенерированного открытого ключа. Остальные узлы вычисляются путем получения хеша от конкатенации (склеивания) дочерних узлов. Таким образом рассчитывается все дерево до корня. Пусть есть 4 пары ключей, дерево Меркла рассчитывается вычислением 7-ми хешей (см. рисунок выше).

Особенностью дерева Меркла является то, что существование любого узла или листа может быть криптографически доказано путем вычисления корня.

Подпись сообщения создается при помощи закрытого ключа из выбранной пары ключей.

Проверка подписи подразумевает вычисление корня на основе переданных параметров и сравнение с ним как с многоразовым публичным ключом. Этими параметрами являются:

• подпись;
• корень;
• одноразовый ключ, закрытой частью которого было подписано сообщение;
• хеши из дерева, лежащие на пути следования от выбранного листа к корню.

При использовании одноразовых подписей Меркла или Винтерница нет необходимости передавать отдельно выбранный одноразовый открытый ключ, поскольку его можно получить из подписи сообщения. Достаточно передать его номер, отражающий его положение в дереве. Например, на рисунке выше передаваемыми параметрами будут: подпись, корень, номер листа — 0 (номер листа с ключом ) и хеши и . При выполнении проверки подписи из нее будет получен открытый ключ , соответственно, и хеш . Хеши и позволят вычислить . А хеши и позволят вычислить корень , который можно будет сравнить со значением переданного корня.

Дерево Меркла, составленное и рассчитанное из открытых ключей, позволяет вместо публикации всего их множества опубликовать лишь корень дерева. Это увеличивает размер подписи за счет включения части дерева в подпись, но дает возможность используя только 1 хеш проверить множество подписей. Так, при глубине дерева можно подписать сообщений.

Дерево Меркла для ключей на базе алгоритма эллиптических кривых используется в Биткойн и Ethereum, о последнем с рассмотрением дерева Меркла есть отличная статья.

Гипердеревья

Основным недостатком базовой схемы Меркла является то, что количество доступных подписей ограничено, и все пары ключей одноразовых подписей должны быть сгенерированы до вычисления дерева Меркла. Генерация ключей и время подписывания растут экспоненциально относительно высоты дерева. Отсрочить генерацию новых ключей, а также увеличить количество доступных пар возможно при использовании гипердерева.ПодробнееГипердерево представляет собой структуру, состоящую из деревьев Меркла. В этой структуре по назначению выделяются 2 типа деревьев: дерево сертификации и дерево подписи. Дереву подписи соответствуют ключи, используемые для подписывания сообщений. Дереву сертификации соответствуют ключи для подписывания корней деревьев подписи. Таким образом, деревья подписи являются дочерними к дереву сертификации (см. рисунок ниже).

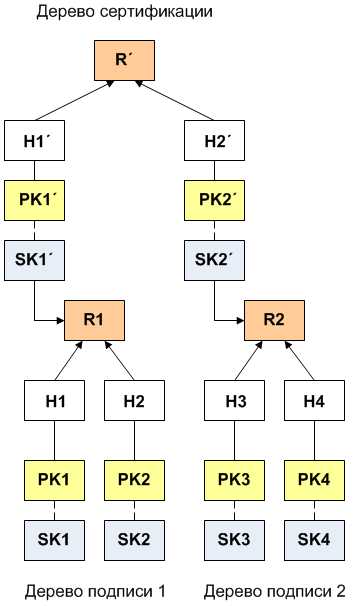
Для проверки подписи сообщения в этом случае передаются те же параметры, что и для обычного дерева Меркла, но с обоих деревьев. Таким образом, подпись и ее проверка становятся несколько сложнее, однако появляется возможность гибко расширять структуру. В то время как размер и количество подписей для каждого дополнительного дерева растет линейно, общий объем подписей гипердерева растет экспоненциально.

Нет необходимости строить гипердерево симметричным. Всегда можно дополнить его слоями новых деревьев подписи. Таким образом, подписи блока транзакций будут изначально небольшого размера, который будет возрастать по мере увеличения глубины гипердерева.

Расширенная структура дерева Меркла (XMSS)

Полное описание схемы выходит далеко за рамки данной статьи, подробнее можно прочесть здесь. Коснусь лишь базовых представлений и характеристик. Схема XMSS как и дерево Меркла позволяет расширять одноразовые подписи. Использование битовой маски с применением исключающего ИЛИ (XOR) дочерних узлов до конкатенации хешей в родительский узел позволяет повысить устойчивость к коллизиям применяемых хеш-функций. Так, при использовании SHA-256 в качестве хеш-функции в сочетании с расширенной схемой Винтерница с параметром безопасности (W-OTS+) позволяет увеличить безопасность с 128 до 196 бит. Согласно Ленстра, 196-битной защиты достаточно, чтобы считать ее безопасной против атаки путем простого перебора до 2169 года. При всех достоинствах схемы XMSS ее основным недостатком является длительное время генерации ключа.

В настоящее время существуют и другие схемы расширения дерева Меркла (GMSS, CMSS), которые в сочетании с алгоритмами одноразовой подписи также могут быть использованы в блокчейне, устойчивом к атакам с применением квантового компьютера.

Часть 3. Реализация идей

Проект квантово-устойчивого блокчена — QRL

Во второй половине 2016 года доктором наук П. Ватерлендом создается группа по разработке блокчейна устойчивого как классическим атакам, так и к атакам с применением квантового компьютера. По результатам разработки теоретической части в конце того же года в открытый доступ выложен главный документ разрабатываемого блокчейна — «белая книга» (white paper). В настоящий момент документ доступен на нескольких языках, включая русский.

Основные характеристики QRL

1. Схема подписи и безопасность
Применяется схема подписи на основе алгоритма расширенной подписи Винтерница (W-OTS+, w = 16, SHA-256) на базе связных структур XMSS. Такой подход позволяет генерировать адреса с возможностью подписи, избегая длительной вычислительной задержки, наблюдаемой при создании гигантских конструкций XMSS. Обеспечивает 196-битную защиту с прогнозируемой безопасностью против атаки путем простого перебора до 2169 года.

2. Алгоритм консенсуса — доказательство работы (proof-of-work)
В первой итерации основной сети анонсирован алгоритм консенсуса proof-of-work.

3. Плавающая комиссия
Боʼльшие размеры транзакций по сравнению с другими блоками цепочки транзакций требуют оплаты для каждой транзакции. По мнению Ватерленда, рынки с искусственной комиссией (например, Биткойн) не нужны и противоречат идеалу открытого блокчейна. Каждая транзакция, если она сопровождается минимальной оплатой, должна быть такой же действительной, как и любая другая. Размер минимальной оплаты, приемлемой для майнеров, должен быть плавающим и устанавливаться рынком. Т.е. узлы (майнеры) должны конкурентно устанавливать нижнюю границу оплаты между собой. Абсолютное минимальное значение будет соблюдаться на уровне протокола. Таким образом, майнеры будут заказывать транзакции из мемпула для включения в блок по своему усмотрению.

4. Динамическое вычисление вознаграждения за блок
Каждый новый созданный блок будет включать в себя первую транзакцию «coinbase», содержащую адрес майнинга, для которого вознаграждение будет определено как сумма вознаграждения за монетную ставку с общей суммой комиссий за транзакции внутри блока.

5. Время нахождения блоков — 1 минута
Время между блоками в сети Биткойн составляет примерно 10 минут. При требуемых 6-ти подтверждениях это дополнительно увеличивает время ожидания завершения транзакции. Более новые схемы блока цепочки транзакций, такие как Ethereum, улучшены в этом аспекте и выигрывают за счет более короткого времени нахождения блока без потери в безопасности или централизации майнеров из-за высокой скорости появления осиротевших/устаревших блоков.

Для QRL это время нахождение блока составляет 1 минуту.

6. Адаптивный размер блока
Во избежание возможных споров было смоделировано готовое адаптивное решение, базирующееся на предложении Bitpay, которое использует для увеличения размера блока множитель средней величины последних блоков. Использование средней величины не позволяет майнерам манипулировать, включая либо пустые, либо переполненные блоки для изменения среднего размера блока. и будут тогда жесткими консенсусными правилами для сети, которым придется подчиняться. Таким образом, максимальный размер блока можно просто вычислить как: .

7. Денежная единица — квант
Базовой единицей валюты является квант. Каждый квант делится на наименьшие элементы. Ниже представлены названия всех элементов в порядке возрастания:

Таким образом, каждая транзакция с участием части кванта на самом деле очень большое число единиц Шора. Плата за транзакцию рассчитывается и проводится в единицах Шора.

8. Аккаунты и адреса
Балансы пользователя хранится на аккаунтах. Каждый аккаунт является уникальным многократно используемым адресом блока цепочки транзакций, обозначенным строкой, начинающейся с «Q».

Адрес создается посредством выполнения SHA-256 по корню Меркла самого высокого дерева сертификации XMSS. К этому добавляется четырехбайтная контрольная сумма, образованная из первых четырех байтов двойного хеша SHA-256 корня Меркла, и буквы «Q».

Например, в псевдокоде Python это будет описано следующим образом:

Q + sha256(merkle root) + sha256(sha256(merkle root))[: 4]

Типичный адрес аккаунта:
Qcea29b1402248d53469e352de662923986f3a94cf0f51522bedd08fb5e64948af479

Каждый аккаунт имеет баланс, деноминированный в квантах, делимый вплоть до единственной единицы Шора. Адреса с каждой транзакцией используют новую пару ключей одноразовой подписи. Счетчик транзакций, называемый nonce, будет увеличиваться с каждой транзакцией, отправленной с аккаунта. Это позволяет кошелькам, которые не хранят всю цепочку блоков, отслеживать их местоположение в схеме подписи гипердерева с сохранением состояния.

Текущее состояние проекта и планы на будущее

После выпуска «белой книги» группа пополнилась несколькими новыми разработчиками и началась работа над воплощением задуманного в жизнь. На сайте проекта появились регулярные отчеты о проделанной работе. И к апрелю 2017 года уже была запущена тестовая сеть блокчейна QRL. Исходный код проекта выложен на Github. Проект активно обсуждается на Bitcointalk и Reddit.

В мае 2017 было проведено ICO в экосистеме Ethereum. Выпущен токен QRL стандарта ERC20. Всего было выпущено 65 млн. токенов. Из них в обращении находится 52 млн. токенов. Постепенно в течение 200 лет будет выпущено еще 40 млн. монет. Таким образом, общий объем эмиссии составит 105 млн. монет. При запуске основной сети эти токены можно будет обменять на QRL монеты в соотношении 1:1. В настоящий момент токены доступны для покупки на таких биржах как Bittrex, Upbit и Liqui. Котировки QRL, согласно сайту coinmarketcap.com, представлены на рисунках ниже.

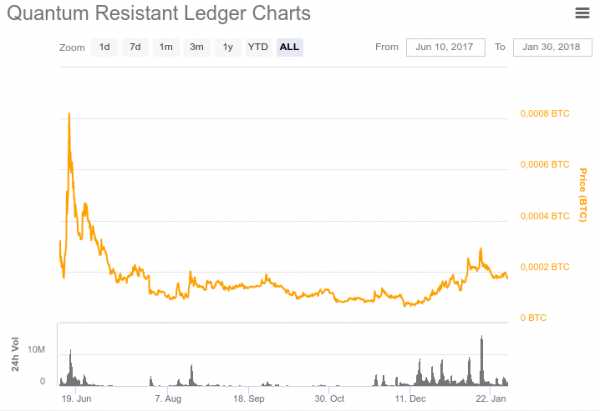
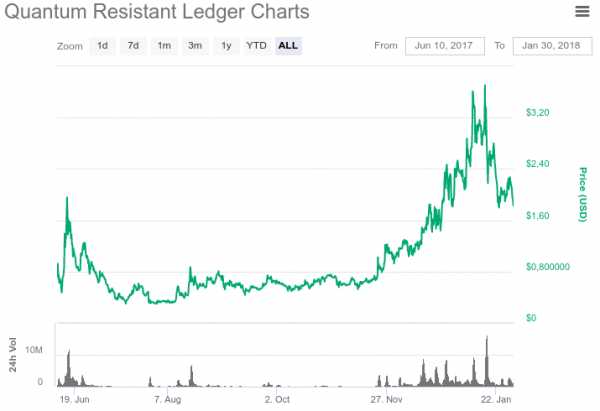
Запуск основной сети намечен на февраль-март 2018.

В дальнейшем планируется изменить алгоритм консенсуса с подтверждения работы на подтверждение доли (proof-of-stake). Ожидаемое безопасное время нахождения блоков будет составлять 15-30 секунд.

Заключение

Прогресс квантовых технологий запущен и его уже не остановить. По мере появления все более производительных квантовых машин спектр решаемых ими задач будет непрерывно расти. Взлом существующей криптозащиты, неприспособленной к атакам квантового компьютера, уже давно является одной из центральных тем множества форумов по безопасности.

QRL — первая блокчейн-технология, призванная решить эту проблему. В будущем, конечно, появятся и другие. Какая из них будет наиболее успешной — покажет время.

Благодарности

Автор выражает благодарность kamnik за подготовку значительной части материала и, особенно, за техническую часть, а также SannX за конструктивную критику и правки.

Ссылки

1. Алгоритм Шора.
2. Разложение числа 15 на простые множители на квантовом компьютере (IBM).
3. Разложение числа 15 на простые множители на квантовом компьютере (MIT).
4. Отчет об экспериментах на 51 кубитном компьютере.
5. Отчет Международной исследовательской группы об устойчивости Биткойна перед квантовым компьютером.
6. Использование алгоритма генерации ключей ECDSA в блокчейне Биткойна.
7. Об устойчивости Биткойна к атакам квантового компьютера.
8. Подтверждение транзакции в сети Биткойн.
9. Информация о комиссиях в сети Bitcoin.
10. Статистика повторного использования Bitcoin-адресов.
11. Квантовый алгоритм Гровера.
12. Расширенная подпись Винтерница.
13. Применение одноразовой подписи Винтерница на базе хеш-функции ГОСТ 34.11-12.
14. Geektimes об Ethereum.
15. Схема XMSS.
16. Ленстра. Выбор размеров криптографических ключей.
17. GMSS.
18. CMSS.
19. Курсы криптовалютных систем.
20. Ежегодный форум по постквантовой безопасности.

Дополнительный материал

1. Опасен ли квантовый компьютер для Биткойна.

Проект QRL

1. Сайт проекта.
2. Белая книга.
3. Презентация.
4. Блог.
5. Исходный код на GitHub.
6. Ветка обсуждения на Bitcointalk.

habr.com

Станет ли квантовый компьютер угрозой для блокчейна?

Автор статьи Натана Шарма является директором Crypto Lotus LLC, криптовалютного хедж-фонда, зарегистрированного в Сан-Франциско, и советником Green Sands Equity, оба из которых имеют вклады в различных цифровых активах. Любые мнения в этом посте являются сугубо авторскими.

При быстром росте стоимости и громких заголовках легко забыть о том, что криптовалюты и блокчейн всё же пока ещё не мейнстрим. Тем не менее, некоторые техно-фэны полагают, что блокчейн может и не стать сильно востребованным в будущем.

Однако размышляя о будущем важно помнить о том, что нет ничего определенного.

Рассматривая угрозы для блокчейна и криптовалют, обычно обращают внимание на усиление регулирования, и в этом есть смысл. В среднесрочной перспективе влияние регуляторов может стать препятствием для более широкого внедрения криптовалют, однако на горизонте может появится и более серьёзная угроза.

Основным преимуществом блокчейна является его безопасность. Технология позволяет распределять реестр транзакций между большой сетью компьютеров так, что никто не может взломать и изменить реестр – и это свойство делает его общедоступным и безопасным.

Но в сочетании с квантовыми вычислениями, другой новой (и сильно раздутой) технологией, неподвластный изменениям реестр блокчейна может оказаться под угрозой.

Квантовый компьютер подобно блокчейну также громко освещается в новостях, а число компаний и исследователей по квантовым вычислениям сейчас продолжает расти. Пока больше внимания уделено аппаратным устройствам, но многие также изучают и программное обеспечение.

Криптография сейчас часто обсуждаемая тема, и квантовый компьютер может создать угрозу для традиционных форм компьютерной безопасности – в первую очередь для криптографии с открытым ключом, которая лежит в основе большинства онлайн-коммуникаций, в том числе и блокчейна.

Но как сегодня работает компьютерная безопасность?

Криптография с открытым ключом использует несколько ключей для шифрования информации: открытый ключ, который можно открыто использовать, и закрытый ключ, известный только владельцу. Любой может зашифровать сообщение с использованием открытого ключа, но только получатель может расшифровать сообщение, используя свой закрытый ключ. Чем сложнее определить соответствие между закрытым и открытым ключом, тем безопаснее сама система.

Лучшие криптографические системы с открытым ключом связывают открытые и закрытые ключи, используя коэффициенты числа, которое является результатом двух очень больших простых чисел. Чтобы определить закрытый ключ только из открытого ключа, нужно было бы вычислить критерии определения этих чисел. Даже если бы традиционный компьютер проверял триллион ключей в секунду – это заняло бы в 785 миллионов раз дольше за 14 миллиардов лет из-за размера этих простых чисел.

Однако, если бы вычислительная мощность увеличилась, тогда у того, кто смог бы ее использовать, появилась бы возможность узнать закрытый ключ на основе открытого ключа. Если бы появилось достаточно компьютеров, которые могли бы генерировать секретные ключи из открытых ключей – то даже самые сильные формы традиционной криптографии с открытым ключом стали бы уязвимы.

Именно тут и появляется квантовый компьютер. Квантовые вычисления основаны на квантовой физике и обладают большей потенциальной мощностью, чем любая другая традиционная форма вычислений.

В квантовых вычислениях используются квантовые биты или «кубиты», которые могут существовать в любой суперпозиции значений между 0 и 1 и поэтому могут обрабатывать гораздо больше информации, чем 0 или 1, что является пределом классических вычислительных систем.

Способность проводить вычисления с помощью кубитов делает квантовые компьютеры на несколько порядков быстрее классических. Google показал, что D—Wave, компьютер с квантовым отжигом, может быть на 100 миллионов раз более быстрым, чем классические компьютеры по определенным специализированным задачам. Сейчас и Google, и IBM работают над своими квантовыми компьютерами.

Кроме того, хотя существует лишь несколько алгоритмов квантовых вычислений, один из самых известных – алгоритм Шора – позволяет быстро разложить большие простые числа. Именно поэтому рабочий квантовый компьютер теоретически может разрушить сегодняшнюю криптографию с открытым ключом.

Квантовых компьютеров, способных к быстрому факторингу чисел, пока нет. Однако, если квантовые вычисления продолжат развиваться, в конечном итоге они достигнут и этого. И когда это событие произойдет – оно будет представлять угрозу для существования криптографии с открытым ключом, а технология блокчейн вместе с биткойном может стать уязвимой.

Значит, безопасный блокчейн станет ненужным в постквантовом мире? Станет ли появление квантовых компьютеров поводом отказаться от блокчейна?

И да и нет, если к этому времени будет разработано решение.

Агентство национальной безопасности США в 2015 году объявило о том, что планирует разработку квантово-устойчивых криптографических систем. Криптографы работают над квантово-устойчивой криптографией, и уже есть блокчейн-проекты, в которых реализована квантово-устойчивая криптография. Например, команда Quantum Resistant Ledger работает над созданием такого блокчейна прямо сейчас.

Что делает такую «постквантовую» криптографию квантовоустойчивой? Возможность генерировать закрытые ключи из открытых ключей способами, которые намного более математически сложны, чем традиционная простая факторизация.

Команда Quantum Resistant Ledger работает над внедрением криптографии на основе хэшей в форме постквантовой криптографии. В криптографии на основе хэша закрытые ключи генерируются из открытых ключей, используя сложные криптографические структуры на основе хэша, а не просто факторизацию чисел. Таким образом, связь между открытым и закрытым ключами намного сложнее, чем в традиционной криптографии с открытым ключом, и станет гораздо менее уязвимой для квантового компьютера, использующего алгоритм Шора.

Эти постквантовые криптографические схемы не нужно запускать на квантовых компьютерах. Quantum Resistant Ledger — это блокчейн-проект, работающий над реализацией постквантовой криптографии. Остается увидеть, насколько успешными он станет, когда полномасштабные квантовые вычисления станут реальностью.

Также необходимо отметить, что квантовые вычисления угрожают абсолютно всем системам компьютерной безопасности, которые основаны на криптографии с открытым ключом, а не только блокчейну. Все системы безопасности, в том числе и блокчейн-системы, должны учитывать постквантовую криптографию для обеспечения безопасности данных. Но самым простым и эффективным способом может быть замена традиционных систем таким блокчейном, в котором реализирована квантовоустойчивая криптография.

Оригинальная статья Is Quantum Computing an Existential Threat to Blockchain Technology? опубликована в блоге SingularityHub

coinspot.io