Математическая формула биткоина – Математика Биткойна: Теория |

Математика Биткойна: Теория |

Одна из причин, почему Биткойн многих сбивает с толку, заключается в том, что эта технология пересматривает одну из базовых концепций человеческого общества: понятие собственности.

В традиционном смысле, если вы являетесь собственником чего-либо: будь то дом или денежная сумма — это означает, что либо эта вещь находится у вас лично, вы ей владеете и распоряжаетесь непосредственно, либо вы поручили управление ей доверенному третьему лицу, такому как банк.

С Биткойном эта простая схема не работает. Сами по себе биткойны не хранятся ни централизованно, ни локально — и поэтому нельзя сказать, кто отвечает за их доверенное хранение. Биткойны существуют лишь как записи в распределенной бухгалтерской книге, называемой блокчейном, копии которой распределены среди добровольной сети подключенных компьютеров. Быть «владельцем» биткойнов просто означает иметь возможность передать контроль над этими записями кому-то еще, зафиксировав факт этой передачи на блокчейне. Что дает вам эту способность? Эксклюзивный доступ к паре ключей ECDSA: секретному и публичному. Хорошо, но что

конкретно это означает, и почему это вдруг гарантирует безопасность этих самых биткойнов?

Давайте-ка попробуем заглянуть под капот.

Что это за ECDSA такая?

ECDSA — это акроним для Алгоритма Цифровой Подписи с Эллиптическими Кривыми. Это процесс, который использует эллиптические кривые и конечные поля, чтобы «подписать» данные таким образом, что третьи лица могут легко проверить подлинность подписи, но при этом сам подписывающий оставляет за собой эксклюзивную возможность создавать подписи. В случае Биткойна «данные», которые подписываются — это транзакция, которая передает право собственности на биткойны.

ECDSA имеет две отдельные процедуры для подписи и ее проверки. Каждая процедура представляет собой алгоритм, состоящий из нескольких арифметических операций. Алгоритм подписи использует секретный ключ, а алгоритм проверки использует только открытый ключ. Мы покажем это на примере позже.

Но для начала давайте пройдем ускоренный курс молодого бойца по эллиптическим кривым и конечным полям.

Эллиптические кривые

В эллиптических кривых нет ничего сложного. Алгебраически каждая такая кривая может быть представлена как уравнение вида:

y² = x³ + ах + b

Для а = 0 и b = 7 (а это именно та версия, которую использует Биткойн) эта кривая выглядит так:

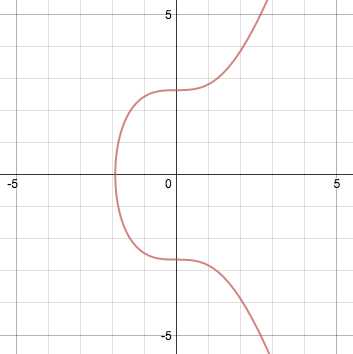
Эллиптические кривые имеют некоторые полезные свойства. Например, не-вертикальная прямая, пересекающая кривую в двух точках, всегда будет пересекать ее и в третьей точке, лежащей на кривой. Другим свойством является то, что если не-вертикальная прямая является касательной к кривой в одной из точек, то она обязательно пересекает кривую еще ровно в одной точке.

Мы можем использовать эти свойства, чтобы определить две операции над точками, составляющими кривую: сложение точек и удвоение.

Для сложения точек

, P + Q = R мы проводим через точки P и Q прямую, которая, по свойствам эллиптических кривых, пересекает кривую в некоторой третьей точке R‘. Затем мы находим точку на кривой, симметричную точке R‘ относительно оси X. Именно эта точка R и будет считаться суммой P и Q. Это легче всего понять, глядя на следующую схему:

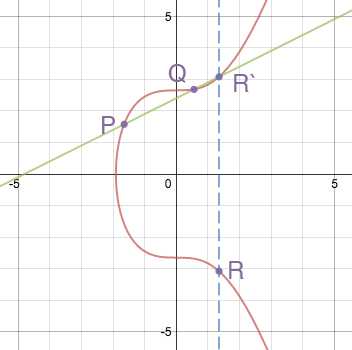
Это все хорошо, но как бы нам сложить точку саму с собой? Для этого определяется операция удвоения точки, P + P = R. При удвоении мы проводим прямую, касательную к данной эллиптической кривой в точке P, которая, согласно свойствам кривой, должна пересекать ее еще в одной точке R

‘. Точка R, симметричная R‘ относительно оси X, и будет считаться точкой удвоения P. На графике это выглядит следующим образом:

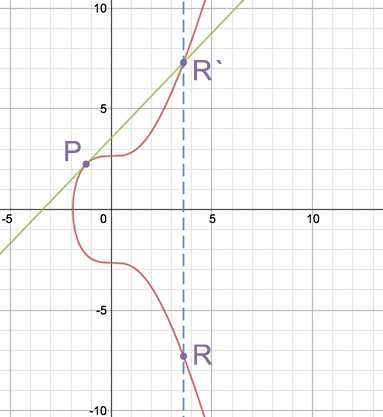
Эти две операции можно использовать, чтобы определить операцию скалярного умножения, R = a P, определяемую как добавление точки Р самой к себе a раз. Например:

R = 7P
R = P + (P + (P + (P + (P + (P + P)))))

Процесс скалярного умножения, как правило, можно упростить, используя комбинацию сложения и удвоения точек. Например:

R = 7P
R = P + 6P
R = P + 2 (3P)
R = P + 2 (Р + 2P)

Здесь операция 7P была разбита на два этапа удвоения точек и два сложения точек — в итоге, вместо 7 операций нужно произвести всего четыре.

Собственно, теперь вы знаете об эллиптических кривых все, что о них стоит знать.

Конечные поля

Теперь поговорим немного о конечных полях. Конечное поле, в контексте ECDSA, можно рассматривать как заданный диапазон положительных чисел. Любые операции должны осуществляться в рамках этого диапазона — если же результат операции выходит за пределы этого диапазона, мы не расстраиваемся, а просто по окончании диапазона возвращаемся к его началу и продолжаем считать как ни в чем ни бывало. Таким образом, результат все равно окажется внутри нашего диапазона, как бы он ни хотел из него выбраться.

Самый простой способ проиллюстрировать это — расчет операции «остаток от целочисленного деления», или оператор модуло (MOD). Например, 9/7 дает 1 с остатком 2:

9 MOD 7 = 2

Здесь мы имеем конечное поле от 0 до 6, и все операции по модулю 7, над каким бы числом они не осуществлялись, дадут результат попадающий в этот диапазон.

Скрещиваем кривые с полями

ECDSA использует не просто эллиптические кривые, а эллиптические кривые в контексте конечного поля, что значительно меняет их ​​внешний вид. Причем, меняет его так, что теперь эти самые кривые даже родная мама не узнает. Допустим, та же самая красивая эллиптическая кривая Биткойна, y² = x³ + 7, которая изображена выше, но только определенная на конечном поле по модулю 67, выглядит как такая вот странная крякозябра:

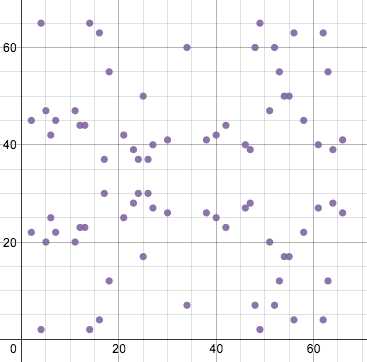
Однако заметим в ее оправдание, что, хотя она и стала неузнаваемой для непосвященных, лежащие в основе этой «кривой» уравнения или ее особые свойства ничуть не изменились. Просто теперь это множество точек, в которых все х и у значения представляют собой целые между 0 и 66 Отметим также, что «кривая» по-прежнему сохраняет свою горизонтальную симметрию.

Правда, процесс операций над точками: сложения и удвоения — сейчас будет немного отличаться визуально. «Прямые линии», нарисованные на этом графике, теперь будут оборачиваться «вокруг поля», как только они достигнут магического барьера 67, как в древней аркадной игре «Asteroids», и продолжаться с другого его конца, сохраняя прежний наклон, но со сдвигом. Поэтому сложение точек (2, 22) и (6, 25) в данном дискретном варианте выглядит следующим образом:

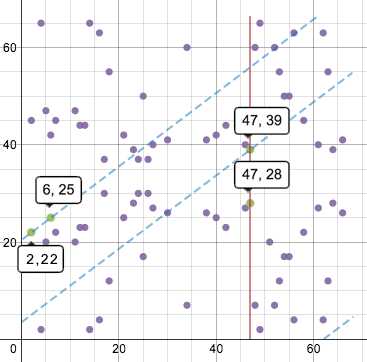
«Оборачивающаяся прямая», проходящая через эти две точки, в итоге уперлась в третью точку (47, 39), а симметричная ей «относительно оси X» будет (47, 28). Вот эта-то точка и станет результатом нашей операции.

Применим свою математическую мудрость к криптографии

Чтобы использовать ECDSA, такой протокол как Биткойн должен зафиксировать набор параметров для эллиптической кривой и ее конечного поля, чтобы эти параметры знали и применяли все пользователи протокола. Иначе каждый будет решать свои собственные уравнения, которые не будут сходиться друг с другом, и они никогда ни о чем не договорятся.

Эти зафиксированные параметры включают в себя уравнение кривой, значение модуля поля и базовую точку, которая лежит на кривой. Последним параметром является порядок базовой точки, который в графическом виде можно представить себе как количество раз, которое базовая точка может быть прибавлена к себе до тех пор, пока ее касательная кривая не станет вертикальной. Этот параметр подбирается таким образом, чтобы он являлся очень 

большим простым числом.

Для всех этих параметров Биткойн использует очень-очень большие (ну просто офигенно невообразимо огромные) числа. Это важно. На самом деле, все практические применения ECDSA используют огромные числа. Ведь безопасность этого алгоритма опирается на то, что эти значения слишком большие, чтобы подобрать что-то простым перебором или «брутфорсом».

В случае Биткойна эти значения таковы (запись чисел дана не в десятичном, а в более компактном шестнадцатеричном виде, привычном программистам):

Уравнение эллиптической кривой: y² = x³ + 7

Простой модуль = 2²⁵⁶ — 2³² — 2⁹ — 2⁸ — 2⁷ — 2⁶

— 2⁴ — 1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F

Базовая точка = 04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8

Порядок = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141

Кто выбрал эти цифры, и почему? Большое количество исследований и изрядная интрига всегда окружают выбор соответствующих параметров. В конце концов, большое и, казалось бы, случайное число может скрывать в себе какую-нибудь «заднюю дверцу» для упрощения вычислений, которая может быть доступна только посвященным. Если вкратце, данная конкретная реализация ECDSA известна как

secp256k1 и является частью семейства стандартов, предлагаемых для использования в криптографии.

Вооружившись всеми этими базовыми знаниями, в следующей статье мы будем готовы применить эту математику к Биткойну и выяснить, наконец, что же там происходит в недрах нашего биткойн-клиента, когда мы нажимаем на кнопку «Оплатить». Ну а пока вы ждете второй части, можете слегка освежить свои знания относительно анатомии биткойн-адресов и транзакций. А если вы разработчик, то можно полюбопытствовать, что же там происходит внутри этого таинственного API биткойн-протокола.

(Продолжение следует)

Источник: Coindesk

Aвтор: Eric Rykwalder

Поделиться ссылкой:

Related

bitnovosti.com

Математические основы биткойн-блокчейна / Bitfury Group corporate blog / Habr

Сегодня биткойн продолжает набирать популярность, а индустрия разрабатывать все новые приложения для работы с криптовалютой. Одной из причин такой популярности является строгая математическая база, на которой строится биткойн.

Благодаря этому система функционирует в условиях полного отсутствия доверия между участниками сети, исключая воздействие человеческого фактора.

Поэтому в сегодняшней статье мы бы хотели поговорить о математических основах биткойн-блокчейна — эллиптических кривых, ECDSA и ключах.

/ Изображение Hernán Piñera CC BY

Фундаментальной частью биткойна являются криптографические алгоритмы. В частности, алгоритм ECDSA — Elliptic Curve Digital Signature Algorithm, который использует эллиптические кривые (elliptic curve) и конечные поля (finite field) для подписи данных, чтобы третья сторона могла подтвердить аутентичность подписи, исключив возможность её подделки. В ECDSA для подписи и верификации используются разные процедуры, состоящие из нескольких арифметических операций.

Эллиптические кривые

Эллиптическая кривая над полем K — это кубическая кривая над алгебраическим замыканием поля K, задаваемая уравнением третьей степени с коэффициентами из поля K и «точкой на бесконечности». Одной из форм эллиптических кривых являются кривые Вейерштрасса.

y² = x³ + ax + b

Для коэффициентов a = 0 и b = 7 (используемых в биткойне), график функции принимает следующий вид:

Эллиптическая кривая

Эллиптические кривые имеют несколько интересных свойств, например, невертикальная линия, пересекающая две некасательные точки на кривой, пересечет третью точку на кривой. Суммой двух точек на кривой P + Q называется точка R, которая является отражением точки -R (построенной путем продолжения прямой (P; Q) до пересечения с кривой) относительно оси X.

Сумма двух точек на кривой (источник)

Если же провести прямую через две точки, имеющие координаты вида P (a, b) и Q (a, -b), то она будет параллельна оси ординат. В этом случае не будет третьей точки пересечения. Чтобы решить эту проблему, вводится так называемая точка на бесконечности (point of infinity), обозначаемая как O. Поэтому, если пересечение отсутствует, уравнение принимает следующий вид P + Q = O.

Если мы хотим сложить точку саму с собой (удвоить её), то в этом случае просто проводится касательная к точке Q. Полученная точка пересечения отражается симметрично относительно оси X.

Удвоение точки (источник)

Эти операции позволяют провести скалярное умножение точки R = k*P, складывая точку P саму с собой k раз. Однако отметим, что для работы с большими числами используются более быстрые методы.

Эллиптическая кривая над конечным полем

В эллиптической криптографии (ECC) используется такая же кривая, только рассматриваемая над некоторым конечным полем. Конечное поле в контексте ECC можно представить как предопределенный набор положительных чисел, в котором должен оказываться результат каждого вычисления.

y² = x³ + ax + b (mod p)

Например, 9 mod 7 = 2. Здесь мы имеем конечное поле от 0 до 6, и все операции по модулю 7, над каким бы числом они ни осуществлялись, дадут результат, попадающий в этот диапазон.

Все названные выше свойства (сложение, умножение, точка в бесконечности) для такой функции остаются в силе, хотя график этой кривой не будет походить на эллиптическую кривую. Эллиптическая кривая биткойна, y² = x³ + 7, определенная на конечном поле по модулю 67, выглядит следующим образом:

Эллиптическая кривая биткойна, определенная на конечном поле по модулю 67 (источник)

Это множество точек, в которых все значения х и у представляют собой целые числа между 0 и 66. Прямые линии, нарисованные на этом графике, теперь будут как бы «оборачиваться» вокруг поля, как только достигнут барьера 67, и продолжатся с другого его конца, сохраняя прежний наклон, но со сдвигом. Например, сложение точек (2, 22) и (6, 25) в этом конкретном случае выглядит так:

Сложение точек (2, 22) и (6, 25) (источник)

Если хотите посмотреть, как выглядят другие эллиптические кривые, то поэкспериментировать можно на этом сайте.

ECDSA в биткойне

В протоколе биткойна зафиксирован набор параметров для эллиптической кривой и её конечного поля, чтобы каждый пользователь использовал строго определенный набор уравнений. Среди зафиксированных параметров выделяют уравнение кривой (equation), значение модуля поля (prime modulo), базовую точку на кривой (base point) и порядок базовой точки (order). О вычислении порядка базовой точки вы можете почитать здесь. Этот параметр подбирается специально и является очень большим простым числом.

В случае биткойна используются следующие значения:

Уравнение эллиптической кривой: y² = x³ + 7

Простой модуль: 2²⁵⁶— 2³² — 2⁹ — 2⁸ — 2⁷ — 2⁶ — 2⁴ — 1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F

Базовая точка:

04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8

Жирным шрифтом выделена координата X в шестнадцатеричной записи. За ней сразу следует координата Y.

Порядок: FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141

Этот набор параметров для эллиптической кривой известен как secp256k1 и является частью семейства стандартов SEC (Standards for Efficient Cryptography), предлагаемых для использования в криптографии. В биткойне кривая secp256k1 используется совместно с алгоритмом цифровой подписи ECDSA (elliptic curve digital signature algorithm). В ECDSA секретный ключ — это случайное число между единицей и значением порядка. Открытый ключ формируется на основании секретного: последний умножается на значение базовой точки. Уравнение имеет следующий вид:

Открытый ключ = секретный ключ * G

Это показывает, что максимальное количество секретных ключей (следовательно, биткойн-адресов) — конечно, и равняется порядку. Однако порядок является невероятно большим числом, так что случайно или намеренно подобрать секретный ключ другого пользователя нереально.

Вычисление открытого ключа выполняется с помощью тех же операций удвоения и сложения точек. Это тривиальная задача, которую обычный персональный компьютер или смартфон решает за миллисекунды. А вот обратная задача (получение секретного ключа по публичному) — является проблемой дискретного логарифмирования, которая считается вычислительно сложной (хотя строгого доказательства этому факту нет). Лучшие известные алгоритмы ее решения, вроде ро Полларда, имеют экспоненциальную сложность. Для secp256k1, чтобы решить задачу, нужно порядка 2¹²⁸ операций, что потребует времени вычисления на обычном компьютере, сопоставимого со временем существования Вселенной.

Когда пара секретный/публичный ключ получена, её можно использовать для подписи данных. Эти данные могут быть любой длины. Обычно первым шагом выполняется хеширование данных с целью получения уникального значения с числом битов, равным битности порядка кривой (256). После хеширования, алгоритм подписи данных z выглядит следующим образом. Здесь, G — базовая точка, n — порядок, а d — секретный ключ.

• Выбирается некоторое целое k в пределах от 1 до n-1
• Рассчитывается точка (х, у) = k * G с использованием скалярного умножения
• Находится r = х mod n. Если r = 0, то возврат к шагу 1
• Находится s = (z + r * d) / k mod n. Если s = 0, то возврат к шагу 1
• Полученная пара (r, s) является нашей подписью

После получения данных и подписи к ним, третья сторона, зная публичный ключ, может их верифицировать. Шаги для проверки подписи такие (Q — открытый ключ):

• Проверка, что и r, и s находятся в диапазоне от 1 до n-1
• Рассчитывается w = s^-1 mod n
• Рассчитывается u = z * w mod n
• Рассчитывается v = r * w mod n
• Рассчитывается точка (x, y) = uG + vQ
• Если r = x mod n, то подпись верна, иначе — недействительна

В самом деле,

uG + vQ = u + vdG = (u + vd)G = (zs^-1 + rds^-1)G = (z + rd) s^-1G = kG

Последнее равенство использует определение s на этапе создания подписи.

Безопасность ECDSA связана со сложностью задачи поиска секретного ключа, описанной выше. Помимо этого, безопасность исходной схемы зависит от «случайности» выбора k при создании подписи. Если одно и то же значение k использовать более одного раза, то из подписей можно извлечь секретный ключ, что и произошло с PlayStation 3. Поэтому современные реализации ECDSA, в том числе используемые в большинстве биткойн-кошельков, генерируют k детерминировано на основе секретного ключа и подписываемого сообщения.

P.S. Bitfury Group Russia в Vk и Fb.

habr.com

Что есть биткоин с точки зрения математики

«Оборачивающаяся прямая», проходящая через эти две точки, в итоге уперлась в третью точку (47, 39), а симметричная ей «относительно оси X» будет (47, 28). Вот эта-то точка и станет результатом нашей операции.

Применим свою математическую мудрость к криптографии

Чтобы использовать ECDSA, такой протокол как Биткойн должен зафиксировать набор параметров для эллиптической кривой и ее конечного поля, чтобы эти параметры знали и применяли все пользователи протокола. Иначе, каждый будет решать свои собственные уравнения, которые не будут сходиться друг с другом, и они никогда ни о чем не договорятся.

Эти зафиксированные параметры включают в себя уравнение кривой, значение модуля поля, и базовую точку, которая лежит на кривой. Последним параметром является порядок базовой точки, который в графическом виде можно представить себе как количество раз, которое базовая точка может быть прибавлена к себе до тех пор, пока ее касательная кривая не станет вертикальной. Этот параметр подбирается таким образом, чтобы он являлся очень большим простым числом.

Для всех этих параметров, Биткойн использует очень-очень большие (ну просто офигенно невообразимо огромные) числа. Это важно. На самом деле, все практические применения ECDSA используют огромные числа. Ведь безопасность этого алгоритма опирается на то, что эти значения слишком большие чтобы подобрать что-то простым перебором или «брутфорсом».

В случае Биткойна, эти значения таковы (запись чисел дана не в десятичном, а в более компактном шестнадцатеричном виде, привычном программистам):

Уравнение эллиптической кривой: y² = x³ + 7

Простой модуль = 2256 — 232 — 29 — 28 — 27 — 26 — 24 — 1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F

Базовая точка = 04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8

Порядок = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141

Кто выбрал эти цифры, и почему? Большое количество исследований, и изрядная интрига, всегда окружает выбор соответствующих параметров. В конце концов, большое и, казалось бы, случайное число может скрывать в себе какую-нибудь «заднюю дверцу» для упрощения вычислений, которая может быть доступна только посвященным. Если вкратце, данная конкретная реализация ECDSA известна как secp256k1 и является частью семейства стандартов, предлагаемых для использования в криптографии.

Вооружившись всеми этими базовыми знаниями, в следующей статье мы будем готовы применить эту математику к Биткойну и выяснить, наконец, что же там происходит в недрах нашего биткойн-клиента, когда мы нажимаем на кнопку «Оплатить». Ну, а пока вы ждете второй части, можете слегка освежить свои знания относительно анатомии биткойн-адресов и транзакций. А если вы разработчик, то можно полюбопытствовать, что же там происходит внутри этого таинственного API биткойн-протокола.

cryptorussia.ru

Формула Биткойна | Bitcoin Times

Люди неподготовленные, сталкиваясь с Биткойном (как и с другими крипто активами), как правило, с трудом воспринимают концепцию подтверждения права собственности, которую переопределяет технология, лежащая в ее основе любого крипто актива — блокчейн (blockchain).

 

Владеть чем-то в традиционном смысле означает быть единоличным собственником объекта, предмета и право собственности определяется тремя признаками, закреплёнными в юридических нормах и, что важно, в процедурах подтверждения:

• владение
• распоряжение
• пользование.

Биткойн не имеет центра эмиссии, центрального хранилища, более того, даже владение биткойном не подразумевает его хранения у собственника! Вся информация о биткойнах хранится в общедоступном блокчейне, у собственника хранится только приватный ключ, позволяющий распоряжаться биткойнами ему принадлежащими (однозначно «привязанными» к приватному ключу). Биткойны существуют как записи в распределенной электронной книге (таблице, базе данных), называемой блокчейном, множественные копии которого находятся в одноранговой сети компьютеров.

 

Право собственности на биткойн означает наличие возможности передать его кому-то другому, создав и подписав приватным ключом запись факта передачи в блокчейне (транзакция Биткойна). Обеспечивает эту возможность и защищает Биткойн сеть от взлома алгоритм ECDSA, позволяющий генерировать пары закрытых (приватного) и открытых (публичного) цифровых ключей. Таким образом сохраняются все три признака права собственности, меняются только процедуры их подтверждения.

 

ECDSA — Elliptic Curve Digital Signature Algorithm — алгоритм цифровой подписи с применением эллиптической кривой. Алгоритм работает так, что подлинность цифровой подписи, поставленной с применением приватного ключа, может быть проверена другой стороной транзакции при помощи открытого ключа. Подписавший сохраняет исключительную способность создавать уникальную подпись. Передача биткойна, реквизиты которого подписаны цифровой подписью — это транзакция, передающая право собственности на него.

 

В ECDSA для подписания и проверки транзакции применяются отдельные процедуры, представляющие собой алгоритм состоящий из нескольких криптографических операций. Для подписи предусмотрено использование закрытого ключа, для проверки используется открытый ключ.

Эллиптические кривые

 Уравнение вида:

 

y² = x³ + ax + b,

 

описывает эллиптическую кривую.

 

Для Биткойна используются коэффициенты a = 0, b = 7  и уравнение принимает вид:  y² = x³ + 7. График такой функции:

 

 

 

 

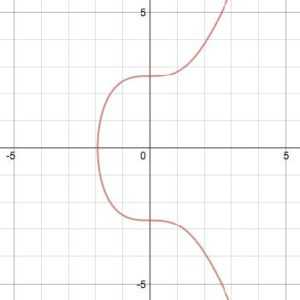
Основные свойства эллиптической кривой:

 

• линия (не вертикальная), пересекающая (не по касательной) две точки на кривой всегда пересечёт третью точку на ней же
• линия, проведённая по касательная к точке кривой, пересечёт ещё одну точку на графике.

 

Можно использовать эти свойства для операций сложения и удвоения точек.

 

Сложение точек P + Q = R определяется как проекция относительно оси X третьей точки R’, являющейся пересечением прямой, проведённой через точки P и Q и графиком эллиптической функции.

 

 

 

 

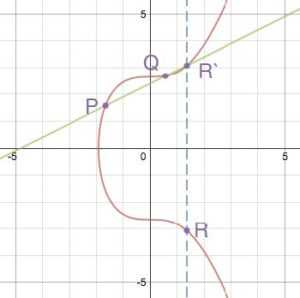
Аналогично, удвоение точки, P + P = R определяется путем нахождения линии, касательной к удвоенной точке, P, и симметричной проекции относительно оси x точки R’ (пересечение касательной с графиком), чтобы получить искомую R.

 

 

 

 

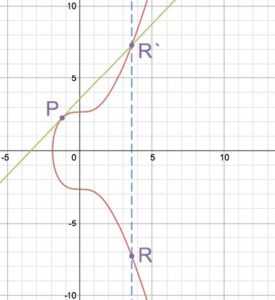
Сложение и удвоение применяются для упрощённого скалярного умножения R = a P. Для Биткойна:

 

R = 7P =P + (P + (P + (P + (P + (P + P)))))), итого 6 операций

 

Упрощённое скалярное умножение:

R = 7P = P + 6P = P + 2 (3P) = P + 2 (P + 2P), итого 4 операции.

Конечные поля

Конечное поле для ECDSA — это известное множество положительных чисел, в которое должны попадать все расчётные значения. Значения не попавшие в множество конечного поля преобразуются (отражаются, обращаются), чтобы попасть в пределы множества.

 

Самый простой способ сделать  такое преобразование — вычислить остатки, произведя целочисленное деление. Например, 9/7 дает 1 с остатком 2:

 

9 mod 7 = 2

 

Здесь конечное поле по модулю 7 с множеством значений находящемся в диапазоне от 0 до 6.

Объединение

ECDSA использует различные эллиптические кривые на конечном поле, что значительно изменяет их внешний вид но не их основные уравнения или специальные свойства. График уравнения приведённого выше, на конечном поле по модулю 67, выглядит так:

 

 

 

 

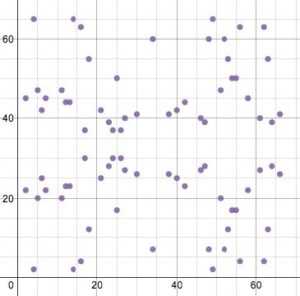
Теперь это набор точек, в которых все значения x и y являются целыми числами от 0 до 66, при этом по-прежнему сохранена горизонтальная симметрия.

 

Визуально график отличается, так как нет непрерывных значений функции (взяты значения попадающие в конечное поле) и поле значений ограничено (графически) квадратом 67×67. Линии, нарисованные на этом графике имеют один и тот же угол наклона. Линия  проведённая по точкам (2, 22) и (6, 25), дойдя до границы значений конечного поля (в данном случае по оси у до значения 67), продолжается (отображается) «появляясь» с другой стороны значений конечного поля (левый нижний край ограничивающего квадрата):

 

 

 

 

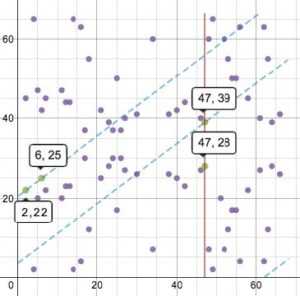
Третья точка — точка пересечения (47, 39), а её симметричное отражение  — точка (47, 28).

 

ECDSA и Биткойн

В криптографии Биткойна применяется фиксированный набор параметров для эллиптической кривой на конечном поле. Для необходимых криптопреобразований используются следующие составляющие:

 

• уравнение эллиптической кривой,
• модуль поля  — p,
• базисная точка — G,
• порядок кривой — n.

 

Базовая точка не выбирается произвольно, а является функцией других параметров. Графически её можно представить, как отображение необходимое число раз, пока угол наклона касательной прямой не будет бесконечным, то есть вертикальной линией. Базовая точка выбирается так, чтобы значение было большим простым числом.

 

Для Биткойна базовая точка — это очень большое число. Безопасность алгоритма напрямую связана с размером числовых массивов, так как, чем больше значения, тем сложнее взломать систему методами перебора (брутфорса) или реверсивного инжиниринга.

 

В случае Биткойна:

 

Уравнение эллиптической кривой: y² = x³ + 7

 

p (модуль эллиптической кривой) = 2²⁵⁶ — 2³² — 2⁹ — 2⁸ — 2⁷ — 2⁶ — 2⁴ — 1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F

 

G (базовая точка) = 04  79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798   483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8, где выделенная подчёркиванием это координата x, оставшаяся часть координата y:

 

x = 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798

y = 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8

 

n (порядок кривой) = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141 — количество точек кривой над конечным полем.

 

Эллиптическая кривая на множестве вещественных чисел (непрерывные числовые значения, в том числе и дробные) не позволяет получить однозначное соответствие (биекцию) исходных данных их образам (хэшам). Чтобы не усложнять, и без того не простые, расчётные методы ещё и округлением, для целей криптографии используются только точки с координатами из множества конечных полей. Исходя из этого, на эллиптической кривой берутся точки со значениями координат попадающими в  конечное поле.

 

Кто и как выбирал именно эти значения для Биткойна, вопрос полемический и открытый. Битвы на форумах происходят до сих пор, то затухая, то снова обостряясь. Приводятся десятки аргументов как за, так и против этих параметров, называемых secp256k1 и являющихся частным случаем множества решений эллиптических кривых над конечными полями. Тем не менее именно secp256k1 предложен и применяется в криптографии Биткойна. Большие значения параметров могут скрывать бэкдор-метод восстановления секретного ключа. Среди аргументов, исключающих эту опасность то, что все константы secp256k1 выбраны известным образом и это значительно снижает вероятность того, что создатель кривой внедрил возможный бэкдор.

---

Если вы через 5 лет будете использовать бумажную валюту, то над вами будут смеяться

---

www.bitcoin-times.ru

Формула Биткоина

Биткоин представляет собой криптографическую сеть, стоимость транзакций в которой можно рассчитать путем деления энергии на определенный временной диапазон. Функция Bitcoin заключается в защите информационного потока с последующим преобразованием энергетической составляющей в более важный сектор — безопасность. В формуле работы Биткоина рассчитывается мощность, равная отношению энергии и времени.

В чем сущность формулы?

Многочисленная «армия» майнеров затрачивает массу энергии и прикладывает серьезные усилия, чтобы защитить каждый новый блокчейн. В процессе работы применяется принцип перебора, обеспечивающий охрану сети от любого постороннего вмешательства. При этом суть выполняемой работы заключается не только в обеспечении защиты блокчейна, но и в подтверждении приведенной информации. От объема энергии, которая затрачивается криптостарателем, напрямую зависит защищенность данных и криптографической сети в целом.

Самая востребованная  валюта должна быть защищена — это аксиома. И главную роль играют правдивые данные, которые нуждаются в безопасном хранении. Получается, что чем больше работы выполняют майнеры, тем выше доверие к информации, представленной в каждом из «кирпичиков» криптосети. В итоге Bitcoin превращает труд в безопасность, без которой ничего не имеет смысла.

Поиск решения является одной из главных задач, ведь на планете Земля признаны только два типа гарантий безопасности. Первый основывается на силе, а другой — на секретности. Вторая составляющая является слабым звеном, ведь все тайное рано или поздно раскрывается. Другое дело — сила, которая исторически является наиболее важным элементом.

Чем обеспечена надежность Bitcoin?

Если рассматривать с позиции физики, суть формулы работы Биткоина легко пояснить. Мощность напрямую зависит от скорости осуществления работы, которую, в свою очередь, можно определить с позиции силы. Вот почему Альткоины, имеющие совершенно иную структуру защиты от подделки, менее важны и не столь хорошо защищены, как первая криптовалюта.

Для обеспечения сохранности актива могут применяться различные инструменты. Одним из них является обычный пароль. Если же попытаться создать схему, в которой больше сотни «прокуроров» определяет сущность правды, над их безопасностью придется поработать. В итоге компрометировать небольшое число «прокуроров» не составит труда. При таком подходе об истине говорить не приходится.

В случае с Bitcoin ситуация выглядит иным образом. Чтобы измерить уровень энергии, требуются временные затраты. Получается, что сама криптовалютная сеть представляет собой новый способ подтверждения уходящего времени и в некотором роде является мерилом истины. К слову, существуют и другие информационные структуры, функционирующие на базе блокчейна, и имеющие аналогичную основу. Одним из ярких примеров является Litecoin. Недостаток Лайткоина только в том, что за ним нет столь мощного показателя хеширования, поэтому и рассчитывать на высокий уровень безопасности не стоит. Тогда какой смысл использовать сеть со слабой защитой, если можно задействовать самую популярную валюту.

В сети Биткоин все события подтверждаются в круглосуточном режиме. Майнеры проверяют каждый блок, что является возможным, благодаря подтверждению истины энергией, а не механизмом секретности. Это значит, что криптосеть является абсолютно честной перед каждым пользователем.

В формуле Биткоина мощность представляет собой частоту, с которой работают майнеры. В основе самой сети лежит особый алгоритм, решив который, можно получить соответствующее доказательство, хоть и зависящее от временного параметра. Современное общество имеет одну общую особенность — оно нуждается в достоверности и надежной валюте.

Важно понимать, что «истина» является мифом. В реальности ее не существует, а сам параметр является субъективным. Какое-то утверждение может быть правильным в определенной мере, но называть его истиной нельзя. Если же изучить структуру Биткоин-сети, принципы ее работы и проверки, можно прийти к мнению о приближении системы к абсолютной истине. Такая особенность открывает большие перспективы.

Надежная валюта имеет большую цену

Почему понятие истинности столь важно? Это легко объяснить. Надежность имеет ключевое значение, ведь пользователь может поставить метку на данные и рассчитать криптографический хеш с последующим помещением правдивой информации в главном распределенном реестре криптовалюты. Получается, что формула Bitcoin дает миру новое понятие истинности. Если размышлять с позиции случайности и применяемых данных, взаимодействие «шахтеров» криптосети как раз и формирует безопасность в отношении данных блокчейна.

Майнеры работают не просто так — их труд щедро оплачивается при формировании каждого последующего блока. Следовательно, участник процесса подключает максимальные мощности для получения требуемой информации. Сам блокчейн Биткоина является уникальной системой, который может регулироваться самостоятельно, то есть каждые десять минут проверяется объем подключенных мощностей. Без наличия временного диапазона система была бы бессмысленной для обычных людей, ведь мы воспринимаем все происходящее через призму времени. Аналогичным образом человек не может рассчитать энергию без применения какой-либо базы.

Интервал, который берется за основу, не важен. Сущность лежит в формуле. Из нее следует, что истина выходит из энергии, разделенной на отдельные временные сегменты. Важно, что процесс построен с учетом протокола, с которым каждый согласен, но для участия в работе системы, необходимо знать правила игры. С помощью этой формулы любой человек, который применяет стандарты, предлагаемые сетью Биткоина, вправе направлять средства и принимать деньги участников криптосети на условиях анонимности. Что касается доверия, с этим нет проблем, ведь оно является непосредственной частью системы.

Чтобы получить доступ к истине, не нужно ничего выдумывать — достаточно пользоваться возможностями криптосети. Каждый участник последней, может быть уверен в правдивости блокчейна и в том, что каждая монета Bitcoin является настоящей.

Безопасность альтчейнов под вопросом

В последние годы появилась тенденция к созданию сетей, которые по структуре имеют много общего с Bitcoin и построены на принципах блокчейна. Существует мнение, что в перспективе любой альтчейн может превзойти по ценности Биткоин. На самом деле эти новые валюты призваны решать какие-то незначительные задачи, а до обеспечения их полной защиты от хакерских атак и достижения высоких стандартов безопасности в целом, будет израсходовано слишком много времени и резервов. Защитный механизм новых альтчейнов построен на секретности, поэтому обойти Биткоин вряд ли получится. Кроме того, решение о расходе средств принимает владелец монет.

Во многих работающих сегодня системах, в том числе в Эфириум, Ripple и прочих, понятие истинности отходит на второй план и имеет более слабую основу, чем в случае с Bitcoin. Чтобы обеспечивать хоть минимальную надежность, пользователи альтчейнов должны прикрепить последние к блокчейну Биткоина. Только так появляется шанс у последних, пробиться в жизнь под «игом» многочисленных конкурентов. С такой же проблемой сталкиваются и банкчейны, которые по своей структуре немногим лучше центральной базы информации.

Приведенных выше причин достаточно, чтобы сделать вывод о бесполезности копирования блокчейна, ведь на первом месте всегда стоит безопасность, а уже потом энергия и время.

allchangers.ru

Математика Биткойна: Практика |

В предыдущей статье мы рассмотрели теоретические основы эллиптической криптографии и поняли, как она работает в принципе. Теперь осталось только применить эти знания на практике: давайте разберемся, как это используется в биткойн-протоколе.

Секретные ключи и открытые ключи

Итак, мы теперь понимаем, как работает дискретная математика эллиптических кривых, и знаем, что в Биткойне используется вариант эллиптической криптографии secp256k1. Teперь можем разобраться с тем, откуда вообще берутся секретные и открытые ключи и как они вообще связаны друг с другом и с биткойн-адресами. Если коротко, в ECDSA секретный ключ — это просто случайное число между 1 и значением порядка. Открытый же ключ получается из секретного при помощи операции скалярного умножения базовой точки на значение секретного ключа. В виде уравнения:

Открытый ключ = секретный ключ * базовая точка

Это показывает, что максимально возможное количество секретных ключей (и, следовательно, биткойн-адресов) — конечно, и равно порядку. Так стало быть, на всех их может не хватить?! Не совсем так: вспомним, что порядок — это действительно большое число — оно невообразимо больше, чем общее число элементарных частиц во всей Вселенной.

Как работает это уравнение в реальности? Вычисление открытого ключа разбивается на ряд операций удвоения точек и сложения точек, начиная с базовой точки.

Напомним, мы работаем с дискретной математикой эллиптических кривых, где сложение точек p + q, чтобы найти их сумму r определяется покомпонентно следующим образом:

c = (q_y — p_y) / (q_x — p_x)
r_x = c² — p_x — q_x
r_y = c (p_x — r_x) — p_y

A операция «удвоения» точки р выглядит следующим образом:

c = (3p_x² + a) / 2p_y
r_x = c² — 2p_x
r_y = c (p_x — r_x) — p_y

Объем вычислений на реальном примере был бы нереально сложным, но мы можем попробовать на примере с небольшими числами, чтобы увидеть, как это работает. Итак, возьмем уравнение кривой Биткойна, но вместо нереально огромных значений порядка, модуля и базовой точки, которые применяются в Биткойне, будем использовать маленькие числа.

Реальный пример из «игрушечной» криптографии

Итак, для удобства создадим себе собственную мини-биткойн-криптографию, например, такую:

Уравнение кривой: y² = x³ + 7
Модуль: 67
Базовая точка: (2, 22)
Порядок: 79

Чтобы показать, что мы не лыком шиты, выберем себе «абсолютно случайный» секретный ключ (из 79 возможных). Ну, пусть это будет 2.

Давайте найдем к нему публичный ключ. Так как мы выбрали простейший «секретный» ключ со значением = 2, нам для этого потребуется лишь одна операция удвоения базовой точки. Очень удобно. Расчет выглядит следующим образом:

c = (3 * 2² + 0) / (2 * 22) mod 67
c = (3 * 4) / (44) mod 67
c = 12 / 44 mod 67

Здесь мы должны провести небольшой трюк, который ранее не объяснялся. Как нам выполнить операцию деления в контексте конечного поля, где результат должен быть целочисленным? Для этого мы должны умножить 12 на величину, обратную к 44. Находить обратную величину в контексте конечных полей не так просто (если хотите изучить этот вопрос подробнее, смотрите здесь), поэтому пока что вам придется поверить мне на слово, что:

44^-1 = 32

Далее все довольно просто:

c = 12 * 32 mod 67
c = 384 mod 67
c = 49

r_x = (49² — 2 * 2) mod 67
r_x = (2401 — 4) mod 67
r_x = 2397 mod 67
r_x = 52

r_y = (49 * (2 — 52) — 22) mod 67
r_y = (49 * (-50) — 22) mod 67
r_y = (-2450 — 22) mod 67
r_y = -2472 mod 67
r_y = 7

Итак, мы определили, что для секретного ключа 2 публичным ключом будет точка (52, 7). Ну, наконец-то! Столько вычислений, и все ради такого-то простого «открытия».

И при всем при том, эта операция — переход от секретного к публичному ключу — по сложности просто ничто по сравнению с попыткой работать в обратном направлении: вывести секретный ключ из публичного ключа. Если для нашего «игрушечного» примера, мы, поднатужившись, еще можем это сделать, в случае с реальной криптографией нас ждет облом. Хотя получить секретный ключ из публичного теоретически и возможно, это является вычислительно невозможным из-за огромных чисел-параметров, используемых в реальной эллиптической криптографии.

Поэтому можно с уверенностью сказать, что переход от секретного ключа к публичному является путешествием в один конец.

Как и секретный ключ, публичный ключ тоже, как правило, представляется в виде шестнадцатеричного числа. Погодите-ка, скажете вы — мы ведь только что узнали, что этот ключ — точка, а не скаляр? Как же его представить в виде одного числа? В несжатом формате публичный ключ — это просто записанные подряд два 256-битных числа, являющиеся его х и у координатами. Мы также можем воспользоваться свойством симметрии эллиптической кривой для получения сжатого публичного ключа — в этом формате он содержит лишь значение координаты х и информацию о том, на какой половине кривой находится точка — на нижней, или на верхней. Из этой информации мы можем восстановить обе координаты, подставив в уравнение кривой.

Подписываем данные секретным ключом

Теперь, когда у нас есть своя собственная пара секретный/публичный ключ (пусть и в игрушечном микро-пространстве эллиптической криптографии), давайте уже наконец подписывать какие-нибудь данные!

Эти данные могут быть любой длины. Обычно первым шагом является хэширование данных, чтобы получить уникальное число, содержащее такое же количество битов (256), как и порядок кривой. Здесь, для простоты, мы пропустим шаг хеширования и сделаем вид, что нам нужно просто подписать набор данных z. Обозначим через G базовую точку, через n — порядок, а d — закрытый ключ. Алгоритм создания подписи выглядит следующим образом:

1. Выберите некоторое целое k в пределах от 1 до n-1.
2. Рассчитайте точку (х, у) = k * G, используя скалярное умножение.
3. Найти r = х mod n. Если r = 0, вернитесь к шагу 1.
4. Найти s = (z + r * D) / k mod n. Если S = 0, вернитесь к шагу 1.
5. Пара (r, s) является нашей подписью

Напомним, в шаге 4, если придется прибегнуть к делению (что в реальной жизни почти всегда происходит), числитель следует умножить на обратную знаменателю величину. А на начальном шаге 1 важно, чтобы k не повторялось в разных подписях, и чтобы его не могла угадать третья сторона. То есть k должен быть либо случайным либо созданным детерминированным процессом, который хранится в тайне от третьих лиц. В противном случае можно было бы вычислить секретный ключ, начиная с шага 4, так как s, z, r, k и n всем известны.

Давайте выберем в качестве наших данных число 17 и подпишем его нашим супер-секретным ключом 2. Итак:

z = 17 (данные)
n = 79 (порядок)
G = (2, 22) (базовая точка)
d = 2 (секретный ключ)

1. Выберем случайное число:

k = rand(1, n — 1)
k = rand(1, 79 — 1)
k = 3 (что, это действительно случайное число!? Ну ладно, ладно, скажем что это тоже «игрушечный» рэндом!)

2. Рассчитаем точку.

Это делается таким же образом, как ранее при вычислении публичного ключа — для краткости опустим подробную арифметику сложения и удвоения.

(x, y) = 3G
(x, y) = G + 2G
(x, y) = (2, 22) + (52, 7)
(x, y) = (62, 63)
x = 62
y = 63

3. Находим r :

r = x mod n
r = 62 mod 79
r = 62

4. Находим s :

s = (z + r * d) / k mod n
s = (17 + 62 * 2) / 3 mod 79
s = (17 + 124) / 3 mod 79
s = 141 / 3 mod 79
s = 47 mod 79
s = 47

Обратите внимание, что выше мы смогли разделить на 3, так как результат был целым числом. В реальной жизни придется искать обратную величину и т.п. – тяжелая вычислительная рутина.

5. Получили подпись:

Нашей подписью является пара (r, s) = (62, 47).

Как и в случае секретных и публичных ключей, эта подпись также обычно представляется в виде шестнадцатеричной строки.

Проверка подписи публичным ключом

Ну хорошо, подпись-то мы получили, что теперь?

Теперь у нас есть данные и наша подпись этих данных. Третья сторона, которая знает наш публичный ключ, может получить наши данные и подпись, и убедиться, что именно мы являемся отправителями. Давайте посмотрим, как это работает.

Обозначив наш открытый ключ Q, шаги для проверки подписи будут следующими:

1. Убедитесь, что r и s находятся в диапазоне от 1 до n-1.
2. Рассчитайте w = s^-1 mod n
3. Рассчитайте u = z * w mod n
4. Рассчитайте v = r * w mod n
5. Рассчитайте точку (x, y) = uG + vQ
6. Убедитесь, что r = x mod n. Если это не так, то подпись недействительна.

Почему эти шаги работают? Мы опускаем здесь формальное доказательство, но вы можете прочитать подробности здесь. Давайте просто прогоним алгоритм вручную и посмотрим, что выйдет. Напомним, наши переменные:

z = 17 (данные)
(r, s) = (62, 47) (подпись)
n = 79 (порядок)
G = (2, 22) (базовая точка)
Q = (52, 7) (публичный ключ)

1. Убедимся, что что r и s находятся в диапазоне от 1 до n-1.

r: 1 <= 62 < 79
s: 1 <= 47 < 79

Да, верно.

2. Рассчитаем w :

w = s^-1 mod n
w = 47^-1 mod 79
w = 37

3. Рассчитаем u :

u = zw mod n
u = 17 * 37 mod 79
u = 629 mod 79
u = 76

4. Рассчитаем v :

v = rw mod n
v = 62 * 37 mod 79
v = 2294 mod 79
v = 3

5. Рассчитаем точку (х, у):

(x, y) = uG + vQ

Это самая веселая часть. Давайте разберем операции удвоения и сложения в uG и vQ отдельно.

uG = 76G
uG = 2(38G)
uG = 2( 2(19G) )
uG = 2( 2(G + 18G) )
uG = 2( 2(G + 2(9G) ) )
uG = 2( 2(G + 2(G + 8G) ) )
uG = 2( 2(G + 2(G + 2(4G) ) ) )
uG = 2( 2(G + 2(G + 2( 2(2G) ) ) ) )

Зацените: с помощью ловкой группировки, мы сводим 75 последовательных операций сложения к всего-то шести операциям удвоения и двум — сложения. И это еще мы работаем на «игрушечных» примерах — представьте себе число операций в «настоящей» криптографии. Или лучше даже не представляйте — не исключено, что просто свихнетесь.

Продолжаем наше захватывающее представление:

uG = 2( 2(G + 2(G + 2( 2( 2(2, 22) ) ) ) ) )
uG = 2( 2(G + 2(G + 2( 2(52, 7) ) ) ) )
uG = 2( 2(G + 2(G + 2(25, 17)  ) ) )
uG = 2( 2(G + 2( (2, 22) + (21, 42) ) ) )
uG = 2( 2(G + 2(13, 44) ) )
uG = 2( 2( (2, 22) + (66, 26) ) )
uG = 2( 2(38, 26) )
uG = 2(27, 40)
uG = (62, 4)

И теперь, все то же для vQ:

vQ = 3Q
vQ = Q + 2Q
vQ = Q + 2(52, 7)
vQ = (52, 7) + (25, 17)
vQ = (11, 20)

Посчитав, складываем их вместе:

(x, y) = uG + vQ
(x, y) = (62, 4) + (11, 20)
(x, y) = (62, 63)

Уфф, кажется закончили. Надеюсь, нигде не ошиблись. Сразу видно, что больше всего работы именно на шаге 5. Осталась уже просто ерунда.

6. Наконец, убедимся, что r = x mod n

r = x mod n
62 = 62 mod 79
62 = 62

Ура, наша подпись действительна!

Заключение

Для тех из вас, кто испугался всех этих страшных уравнений в тексте, и быстренько прокрутил статью до конца, что же мы только что узнали?

Мы выработали некоторую интуицию относительно взаимосвязей, которые существуют между публичными и секретными ключами. Мы увидели, как даже на простейших, «игрушечных» примерах, математика создания эллиптических подписей и их проверки быстро усложняется. Теперь мы можем по достоинству оценить огромную сложность вычислений, которые возникают, когда параметры являются огромными 256-битными числами. Мы увидели, как хитрое применение простых математических процедур создает «односторонние» функции, необходимые для сохранения информационной асимметрии. Именно эта асимметрия позволяет нам доказать права собственности на биткойны, не раскрывая при этом своих секретных ключей.

Если вы прошли через это практическое занятие, то обрели некоторую уверенность в надежности системы — при условии, что знание наших секретных ключей надежно защищено от посторонних.

Как минимум, теперь можно понять, почему так часто повторяется, что права собственности на биткойны «гарантированы математикой».

Если вы хорошо проштудировали эти примеры, то они должны дать вам достаточно уверенности, чтобы сделать следующий шаг и попробовать сделать подобные расчеты самостоятельно (что касается модульной арифметики, то этот калькулятор сильно упрощает жизнь). Мы обнаружили, что прохождение шагов подписания и проверки данных вручную обеспечивает более глубокое понимание той криптографии, которая превращает Биткойн в уникальную форму собственности, непохожую на все, что было до него.

Источник: Coindesk

Aвтор: Eric Rykwalder

Поделиться ссылкой:

Related

bitnovosti.com

Математика и биткоин: Как рассчитать справедливую стоимость 1 BTC | Финансы

Аналитики инвестиционной компании Pugilist Ventures, специализирующейся на цифровых активах и блокчейне, рассказывают о том, что такое коэффициент NVT и как он поможет определить, сколько должна стоить криптовалюта.

Преамбула

Неделю назад известный криптовалютный аналитик Вилли Ву опубликовал статью, в которой заявил, что биткоин (EXANTE: Bitcoin) может подешеветь с текущих уровней до $5500−5700. Главной причиной падения он назвал слишком высокий уровень коэффициента NVT — отношения стоимости сети (рыночная капитализация) к объему проводимых транзакций. По мнению Ву, чтобы оправдать текущую цену, необходимо значительное увеличение объемов операций. Иначе котировки будут вынуждены снизиться до уровня, соответствующего загруженности сети.

Несколько дней спустя управляющий директор Fundstrat Роберт Слеймер, наоборот, выразил оптимизм в отношении биткоина и заявил о скором возобновлении бычьего тренда. В основе его выводов лежит мощная поддержка в окрестности уровня $7000 и перепроданность индикатора RSI.

Что определяет NVT — оценку или скорость обращения

Некоторые аналитики утверждают, что если для оценки блокчейн-сетей достаточно Количественной теории денег, то коэффициент NVT идентичен скорости обращения токена (средняя частота, с которой денежная единица используется для покупки новых отечественных товаров и услуг за определенный период времени, — прим. ред.). Более того, они пришли к выводу, что всплески скорости обращения (как в 2018 году) обычно предшествуют спадам на рынке. Они позволяют очистить систему от «иррационального изобилия», оставшегося от предыдущего бычьего рынка.

При условии сохранения исторических норм «нормальный» диапазон 30-дневной скользящей средней коэффициента NVT биткоина лежит между 10 и 20. Значения выше 20 указывают на чрезмерный энтузиазм на рынке, тогда как значения ниже 10 говорят о недооцененности криптовалюты (конечно, если они не следуют сразу за стремительным ростом).

Кроме того, с помощью простых арифметических вычислений коэффициент NVT позволяет оценить диапазон цен, соответствующий каждой из переменных — сетевой стоимости (рыночной капитализации) и объема транзакций в блокчейне (в долларах США).

Анализ уравнения NVT

Используя формулу NVT, проведем анализ трех сценариев, чтобы установить потенциальный разброс цен биткоина. Будем исходить из предположения, что текущий разрыв между капитализацией и объемом транзакций вернется на исторически «нормальный» уровень. Для этого должен либо возрасти объем операций, либо сократиться рыночная капитализация.

В анализе мы использовали объем операций и рыночную капитализацию по состоянию на 3 июня — 4,4 млрд и 130,3 млрд долларов, соответственно. Применялись следующие уравнения и показатели:

• NVT = Рыночная капитализация / Объем операций;
• Объем операций при NVT = Текущая капитализация / NVT сценария;
• Разница в объемах операций = Текущий объем — Объем, предполагаемый
• сценарием;
• Рыночная капитализация при NVT = Текущий объем операций * NVT сценария;
• Необходимое снижение капитализации = Капитализация по сценарию — Текущая рыночная капитализация;
• Стоимость одного биткоина = Рыночная капитализация по сценарию / Текущее предложение.

Проведя соответствующие расчеты для NVT, равного 10, 15 и 20, мы установили, что для оправдания текущей рыночной цены биткоина объем операций в сети должен значительно возрасти (на 8,5 млрд, 4,2 млрд и 2 млрд долларов, соответственно).

Или должна существенно снизиться рыночная капитализация (на 85,5 млрд, 63,1 млрд и 40,7 млрд долларов, соответственно), чтобы коэффициент NVT вернулся на «нормальные» уровни в 10, 15 и 20.

• В самом консервативном и худшем с точки зрения цены сценарии (NVT = 10) справедливая стоимость биткоина составляет $2618.
• Среднее значение коэффициента NVT (15) дает справедливую цену биткоина, равную $3927.
• В самом оптимистичном сценарии (при NVT = 20) справедливая рыночная цена биткоина, определенная с помощью Количественной теории денег, составляет $5237.

Заключение

У этого анализа есть два недостатка:

1. Рыночная капитализация и объем блокчейн-транзакций взаимосвязаны и влияют друг на друга. Таким образом, метод изначально небезупречен и не позволяет провести оценку с высокой достоверностью.
2. Ежедневно в обращении появляются новые биткоины, поэтому гипотетическая цена криптовалюты в сценариях будет постоянно меняться, влияя на точность оценок.

Используя доступные инструменты анализа, следует согласиться и с Ву и со Слеймером, учитывая, что оценки одного основаны на особенностях коэффициента NVT, а другого — на динамике цен. Однако в долгосрочной перспективе обычно верх одерживают фундаментальные показатели, поэтому рано или поздно цена должна подскочить на фоне значительного интереса со стороны покупателей. Это позитивно повлияет на объемы блокчейн-транзакций, позволит закрыть разрыв и вернуть коэффициент NVT в нормальный диапазон.

Мнение автора может не совпадать с позицией редакции.

Подготовила Евгения Сидорова

ru.ihodl.com