RSA-шифрование на пальцах
RSA-шифрование на пальцахВокруг алгоритмов шифрования с отрытым и закрытым ключом существует множество недопониманий и мистификаций. Здесь я хотел бы предельно коротко и наглядно, с конкретными числами и минимумом формул, показать, как это работает.
Я не вдаюсь в теорию (не очень понятно, на какой уровень подготовки читателя следует рассчитывать), но я уверен, что прочитав эту короткую иллюстрацию, любому человеку будет проще разобраться в формулах и строгих доказательствах.
Итак. Допустим, я хочу получить от вас некие данные. Мы с вам не хотим, чтобы эти данные узнал кто-то, кроме нас. И у нас нет никакой уверенности в надёжности канала передачи данных. Приступим.
Шаг первый. Подготовка ключей
Я должен проделать предварительные действия: сгенерировать публичный и приватный ключ.
- Выбираю два простых числа. Пусть это будет
p=3иq=7. - Вычисляем модуль — произведение наших
pиq: - Вычисляем функцию Эйлера:
φ=(p-1)×(q-1)=2×6=12. - Выбираем число
e, отвечающее следующим критериям: (i) оно должно быть простое, (ii) оно должно быть меньшеφ— остаются варианты: 3, 5, 7, 11, (iii) оно должно быть взаимно простое сφ; остаются варианты 5, 7, 11. Выберемe=5. Это, так называемая, открытая экспонента.
Теперь пара чисел {e, n} — это мой открытый ключ. Я отправляю его
вам, чтобы вы зашифровали своё сообщение. Но для меня это ещё не всё.
Я должен получить закрытый ключ.
Мне нужно вычислить число d, обратное е по модулю φ. То есть
остаток от деления по модулю d×e должен быть
равен 1. Запишем это в обозначениях, принятых во многих языках
программирования: (d×е)%φ=1. Или (d×5)%12=1. d может быть
равно 5 ((5×5)%12=25%12=1), но чтобы оно не путалось с e в дальнейшем повествовании,
давайте возьмём его равным 17. Можете проверить сами, что (17×5)%12 действительно равно 1 (17×5-12×7=1). Итак d=17.
Пара {d, n} — это секретный ключ, его я оставляю у себя. Его
нельзя сообщать никому. Только обладатель секретного
ключа может расшифровать то, что было зашифровано открытым ключом.
Шаг второй. Шифрование
P=19. Кроме него у вас уже есть мой открытый ключ: {e, n} = {5, 21}. Шифрование выполняется по следующему
алгоритму:- Возводите ваше сообщение в степень
eпо модулюn. То есть, вычисляете 19 в степени 5 (2476099) и берёте остаток от деления на 21. Получается 10 — это ваши закодированные данные.
Строго говоря, вам вовсе незачем вычислять огромное число «19 в степени 5». При каждом умножении достаточно вычислять не полное произведение, а только остаток от деления на 21. Но это уже детали реализации вычислений, давайте не будем в них углубляться.
Полученные данные E=10, вы отправляете мне.
Здесь надо заметить, что сообщение P=19 не должно быть больше n=21. иначе ничего не получится.
Шаг третий. Расшифровка
Я получил ваши данные (E=10), и у меня имеется закрытый ключ {d, n} = {17, 21}.
Обратите внимание на то, что открытый ключ не может расшифровать сообщение. А закрытый ключ я никому не говорил. В этом вся прелесть асимметричного шифрования.
Начинаем раскодировать:
- Я делаю операцию, очень похожую на вашу, но вместо
eиспользуюd. ВозвожуEв степень
Заметьте, никто, кроме меня (даже вы!) не может расшифровать ваше сообщение
(E=10), так как ни у кого нет закрытого ключа.
В чём гарантия надёжности шифрования
Надёжность шифрования обеспечивается тем, что третьему лицу
(старающемуся взломать шифр) очень трудно вычислить закрытый ключ
по открытому. Оба ключа вычисляются из одной пары простых чисел
(p и q). То есть ключи связаны между собой. Но установить эту
связь очень сложно. Основной загвоздкой является декомпозиция
модуля n на простые сомножители p и
Постараюсь это показать на примере. Давайте разложим на множители число 360:
- сразу ясно. что оно делится на два (получили 2)
- оставшееся 180 тоже, очевидно чётное (ещё 2)
- 90 — тоже чётное (ещё двойка)
- 45 не делится на 2, но следующая же попытка оказывается успешной — оно делится на три (получили 3)
- 15 тоже делится на 3
- 5 — простое.
Мы на каждом шагу, практически без перебора, получали всё новые и новые множители, легко получив полное разложение 360=2×2×2×3×3×5
Давайте теперь возьмём число 361. Тут нам придётся помучиться.
- оно не чётное
- три — нет, не делится
- пять (допустим, мы поступаем умно и перебираем только простые числа, хотя, на практике, поиск больших простых чисел, сам по себе, является сложной задачей) — не подходит
- семь? — нет.
- …
- и только 19 даст нам ответ: 361=19×19.
При использовании больших чисел, задача становится очень сложной. Это позволяет надеяться, что у взломщика просто не хватит вычислительных ресурсов, чтобы сломать ваши шифр за обозримое время.
А как это всё работает на практике?
Многие читатели спрашивают, как всё это применяется на практике. Давайте рассмотрим чуть более приближенный к жизни пример. Зашифруем и расшифруем слово «КРОТ», предложенное одним из читателей. А заодно, бегло рассмотрим, какие проблемы при этом встречаются и как они решаются.
Сперва сгенерируем ключи с чуть бо́льшими числами. Они не так наглядны, но позволят нам шифровать не только числа от нуля до 20.
Оттолкнёмся от пары простых чисел {p, q} = {17, 19}.
Пусть наш открытый ключ будет {e, n} = {5, 323}, а
закрытый {d, n} = {173, 323}.
Мы готовы к шифрованию. Переведём наше слово в цифровое представление. Мы можем взять просто номера букв в алфавите. У нас получится последовательность чисел: 11, 17, 15, 19.
Мы можем зашифровать каждое из этих чисел открытым
ключом {e, n} = {5, 323}
{d, n} = {173, 323} и он всё расшифрует.Немного о сложностях
На самом деле, изложенный способ шифрования очень слаб и никогда не используется. Причина проста — шифрование по буквам. Одна и та же буква будет шифроваться одним и тем же числом. Если злоумышленник перехватит достаточно большое сообщение, он сможет догадаться о его содержимом. Сперва он обратит внимание на частые коды пробелов и разделит шифровку на слова. Потом он заметит однобуквенные слова и догадается, как кодируются буквы «a», «и», «o», «в», «к»… Путём недолгого перебора, он вычислит дополнительные буквы по коротким словам, типа «но», «не», «по». И по более длинным словам без труда восстановит все оставшиеся буквы.
Таким образом, злоумышленнику не придётся отгадывать ваши секретные ключи. Он взломает ваше сообщение, не зная их.
Чтобы этого не происходило, используются специальные дополнительные алгоритмы, суть которых в том, что каждая предыдущая часть сообщения начинает влиять на следующую.
Упрощённо, это выглядит так. Перед шифрованием, мы применяем
к сообщению правило: b := (b + a) % n. Где a — предыдущая
часть сообщения, а b — следующая. То есть наше сообщение
(11, 17, 15, 19) изменяется. 11 остаётся без изменений.
17 превращается в (11 + 17) % 323 = 28. 15 становится
Последовательность (11, 28, 43, 62) получается «запутанной». Все буквы в ней как бы перемешаны, в том смысле, что на каждый код влияет не одна буква, а все предыдущие.
Тот, кто получит ваше сообщение, должен будет
проделать обратную операцию, со знаком «минус»: b := (b - a) % n. И только тогда он получит коды
букв.
На практике, в исходное сообщение специально добавляются случайные и бессмысленные буквы в начало. Чтобы даже по первому коду было невозможно ничего понять. Получатель просто отбрасывает начало сообщения.
То есть мы можем добавить случайное число в начало и получить (299, 11, 17, 15, 19). После перемешивания получится: 299, 310, 4, 19, 38. После шифрования уже невозможно будет догадаться где была какая буква.
В реальной жизни всё ещё немного сложнее. Блоки, на которые бьётся сообщение длиннее одной буквы. Поэтому, сперва применяются алгоритмы выравнивания, потом алгоритмы разбиения на блоки с перепутыванием, и только потом применяется само RSA-шифрование.
Получатель делает всё в обратном порядке: расшифровывает, «распутывает» блоки и отбрасывает ненужную информацию, добавленную просто для выравнивания (чтобы сообщение можно было разбить на целое число блоков).
Детали и принципы формирования блоков можно почитать тут. Я же в этой заметке хотел рассказать только про RSA. Надесь, удалось.
Отправить
www.michurin.net
Что такое RSA-ключ ЕГАИС? | Меридиан
 Регулятор закона в целях контроля передвижения каждой бутылки алкоголя от производства до покупателя внедрил всероссийскую базу данных. Это обеспечивает прозрачность движения каждой единицы товара, а также помогает бороться с недоимками по фискальным платежам. Для работы в системе ЕГАИС требуется иметь крипто-ключ и сформированный ключ RSA, а также транспортный модуль. Все это необходимо для защищенной работы в системе, чтобы третьи лица не смогли воспользоваться информацией в своих интересах.
Регулятор закона в целях контроля передвижения каждой бутылки алкоголя от производства до покупателя внедрил всероссийскую базу данных. Это обеспечивает прозрачность движения каждой единицы товара, а также помогает бороться с недоимками по фискальным платежам. Для работы в системе ЕГАИС требуется иметь крипто-ключ и сформированный ключ RSA, а также транспортный модуль. Все это необходимо для защищенной работы в системе, чтобы третьи лица не смогли воспользоваться информацией в своих интересах.
Ключ RSA ЕГАИС – что это?
Представляет собой сертификат для защищенного соединения с единой платформой. Система необходима для передачи данных в безопасном режиме. Криптосистема позволяет пользоваться ключом шифрования только соответствующим зарегистрированным субъектам. Все данные зашифрованы от посторонних третьих лиц. РСА-ключ для ЕГАИС записывается на крипто-ключ на веб-ресурсе официального портала. Операция по записи зашифрованных данных предоставляется бесплатно.
В процессе осуществления профессиональной деятельности для каждого юридического подразделения необходимо получить собственный RSA-ключ для работы с использованием Рутокен в ЕГАИС. Перед тем как зарегистрировать соответствующие данные требуется удостовериться, что запущен аппаратный крипто-ключ той компании, для которой формируется сертификат РСА.
Что нужно для формирования ключа RSA ЕГАИС Рутокен
На начальной стадии пользователю потребуется зарегистрироваться на официальном ресурсе. После этого понадобится зайти в Личный кабинет с помощью уже имеющейся электронной подписи. В панели управления необходимо будет выбрать графу «Показать сертификат». После чего вы сможете увидеть все сертификационные материалы со сведениями о ваших точках с указанием всех идентификационных данных. Представленная информация необходима для записи специального RSA-ключа.
На следующем этапе нужно будет перейти в раздел «Получить ключ». На табло вы сможете увидеть перечень пунктов сбыта АП, которые были указаны вами при прохождении процедуры регистрации. Затем вы можете выбрать соответствующий пункт, для которого предназначен специализированный крипто-ключ и выбрать поле «Сформировать ключ». Электронная платформа запросит ввести пароль. В случае какого-либо затруднения вы можете обратиться в службу поддержки на официальном веб-ресурсе.
После того как вы установили или перезаписали РСА сертификат ЕГАИС на Рутокен можно приступать к установке УТМ. Запустив универсальный транспортный модуль, вы сможете приступить к производству и продаже алкоголя в рамках новых положений законодателя. Дополнительно нужно будет позаботиться о приобретении сканеров с целью считывания данных и стабильного осуществления всех процессов на электронной платформе.
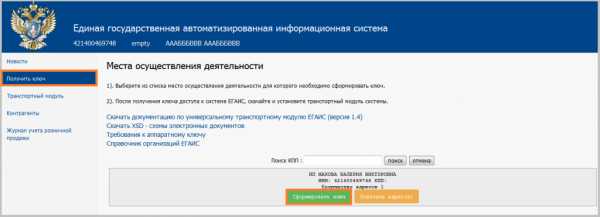
Как обновить сертификат РСА ЕГАИС Рутокен
В связи с обновлением сертификата все субъекты алкорынка обязаны произвести обновление ключа RSA. В самом начале необходимо будет удалить старый сертификат и уже затем установить новый.
- Для владельцев Рутокен. Войти в панель управления, найти поле с именем ключа и выбрать «Удалить». После подтверждения операции и введения pin-кода РСА ЕГАИС Рутокен установленный ранее сертификат удалится.
- Для владельцев Джакарты. Войти в систему администрирования, выбрать поле инициализации, ввести пароль администратора и затем очистить старый сертификат.
После удаления необходимо произвести обновление ключа RSA ЕГАИС Рутокен. Все манипуляции нужно будет выполнить на официальном веб-портале. При формировании ключа вам нужно будет ввести пин-код. Если все идентификационные данные будут введены правильно, сертификат будет зарегистрирован. В случае возникновения каких-либо сложностей при продлении ключа РСА ЕГАИС обратитесь в техподдержку. Специалисты могут подключиться удаленно к вашему компьютерному устройству в целях наиболее оперативного решения вопроса.
Ошибки с RSA-ключом ЕГАИС
 В процессе генерации РСА сертификата могут возникать определенные сложности. В большинстве случаев существуют две причины. Первая – это неполадки на веб-ресурсе. Вторая – некорректные настройки компьютерного оборудования. Для устранения проблем с RSA-ключом ЕГАИС потребуется выполнить следующие действия:
В процессе генерации РСА сертификата могут возникать определенные сложности. В большинстве случаев существуют две причины. Первая – это неполадки на веб-ресурсе. Вторая – некорректные настройки компьютерного оборудования. Для устранения проблем с RSA-ключом ЕГАИС потребуется выполнить следующие действия:
- Выключите все антивирусные программы, установленные на компьютерном оборудовании.
- Позаботьтесь о том, чтобы была установлена более новая версия ОС, например, Windows 7, 8 или 10. При этом желательно, чтобы все действующие обновления уже были запущены.
- Загрузите браузер Internet Explorer самой последней версии.
- Предпримите все усилия, чтобы запустить крипто-плагины ФСРАР-Крипто самой последней модели, а также установить соответствующие драйвера для успешного осуществления операций на электронной платформе.
Если же при обновлении ключа RSA ЕГАИС возникнут какие-либо сложности и не будет появляться графа «Запрос пин-кода», то необходимо в компьютерном оборудовании произвести соответствующие корректировки в настройках. В большинстве случаев неправильные настройки являются следствием невыполнения операций по формированию ключа.
При работе с использованием системы RuToken вам потребуется зайти в Панель управления, где потребуется выбрать Настройки, напротив строки Рутокен вам необходимо выбрать значение Microsoft Base Smart Card Crypto Provider. После этого нужно попробовать еще раз сформировать ключ. Если возникнут сложности, необходимо произвести обновление драйверов.
Помимо этого, проблема возникает при неправильном введении пин-кода. Если вы несколько раз неправильно ввели данные, то носитель может заблокироваться. Тогда вам придется обратиться в удостоверяющий центр. Дополнительно причиной ошибки может стать несоответствие адреса РСА ключа, указанного в лицензии. Если же будет выявление несоответствие данных, нужно будет обратиться в техподдержку Росалкогольрегулирования. С соответствующим запросом можно обратиться как лично, так и через Личный кабинет. Стоит отметить, что в некоторых случаях после внесения корректировок может потребоваться повторное формирование РСА-ключа.
Итак, для успешной работы во всероссийской системе вам помимо крипто-ключа и установки УТМ необходимо позаботиться о формировании RSA-ключа.
meridiant.ru
Шифрование RSA для первокурсников / Habr
Когда я учился программировать, меня всегда раздражало решать на практиках неинтересные задачи. Теперь я преподаю, и мне не хочется, чтобы студенты скучали на моих занятиях.В этой статье я решаю на языке MIT Scheme задачу шифрования и дешифрования методом RSA [1]. По ряду причин, которые рассматриваются в статье, реализация не может использоваться для криптографической защиты информации.
RSA относится к ассиметричным алгоритмам шифрования: если для шифрования используется открытый ключ, то для дешифрования используется закрытый, и наоборот. Первое свойство позволяет кому угодно зашифровать сообщение открытым ключом в адрес владельца закрытого ключа и тем самым обеспечить его конфиденциальность. Второе свойство позволяет владельцу ключа зашифровать хэш сообщения закрытым ключом, чтобы кто угодно мог дешифровать зашифрованный хэш, сравнить его с хэшем сообщения и определить, было ли сообщение модифицровано.
Первый этап генерации ключей — случайный выбор двух достаточно больших простых чисел p и q. Натуральное число x называется простым, если у него есть ровно два различных делителя: 1 и x. Все другие делители числа располагаются на отрезке от 2 до квадратного корня из x, однако достаточно проверять на кратность только простые делители, принадлежащие этому отрезку.
(define (Primes n)
(define (prime? n primes)
(define (iter divisors)
(or (null? divisors)
(let ([divisor (car divisors)])
(or (> (* divisor divisor) n)
(and (< 0 (remainder n (car divisors))) (iter (cdr divisors))))))
)
(iter primes)
)
(define (iter primes i candidate)
(cond
((= i n) primes)
((prime? candidate (reverse primes)) (iter (cons candidate primes) (+ i 1) (+ candidate 1)))
(else (iter primes i (+ candidate 1)))
)
)
(iter '() 0 2)
)
(define primes (Primes 100))
(define p (car primes))
(define q (car (drop 10 primes)))Произведение найденных простых чисел является первым элементом открытого и закрытого ключей. Приведённый алгоритм позволяет найти за разумное время только первые миллион простых чисел. В реализациях RSA, используемых для защиты информации, используются алгоритмы поиска простых чисел, позволяющие найти простые числа с большим числом разрядов; благодаря тому, что лучший известный алгоритм разложения числа на простые множители работает за время, пропорциональное экспоненте от количества разрядов, считается что восстановить пару простых чисел по рассматриваемому элементу открытого ключа невозможно [2].
(define n (* p q))
Для вычисления вторых элементов открытого и закрытого ключей используется величина fi, равная функции Эйлера [3], вычисленной на n. Функция Эйлера от x равна количеству натуральных чисел, не больших x и взаимно простых с ним. Для n это количество будет равно произведению p-1 и q-1.
(define fi (* (- p 1) (- q 1)))
Вторым элементом открытого ключа выбирается случайное число e в диапазоне от 1 до fi, являющееся взаимно простым с fi. то есть таким, что наибольшим общим делителем чисел является 1.
(define (CoprimesLess n)
(define (iter accumulator candidate)
(cond
((= 1 candidate) accumulator)
((= 1 (gcd n candidate)) (iter (cons candidate accumulator) (- candidate 1)))
(else (iter accumulator (- candidate 1)))
)
)
(iter '() (- n 1))
)
(define e (car (drop 5 (CoprimesLess fi))))Для поиска наибольшего общего делителя можно использовать алгоритм Евклида [4].
Одним из объектов, изучаемых теорией чисел, является кольцо вычетов [5]. Кольцо вычетов по модулю k — это целые числа от 0 до k-1 и операции сложения и умножения на нём. Сложение в кольце вычетов (a + b mod k) отличается от сложения в группе целых чисел тем, что если результат сложения становится больше k, из него вычитается k, в результате чего этот результат снова оказывается в кольце. Интуитивно, кольцо получается из отрезка соединением его концов.
Как и в группе целых чисел, умножение в кольце вычетов можно задать при помощи сложения, а возведение в степень — при помощи умножения. Как и в группе целых чисел, получившиеся операции сложения и умножения будут обладать ассоциативностью, то есть:
a + (b + c mod k) mod k = (a + b mod k) + c mod k
a * (b * c mod k) mod k = (a * b mod k) * c mod k
Вторым элементом открытого ключа должно быть число d такое, что его произведение с e в кольце вычетов по модулю n является 1, то есть мультипликативно обратный элемент. Привожу алгоритм поиска такого элемента при помощи расширенного алгоритма Евклида [6].
(define (MultInverseModN a n)
(define (iter a-prev a r-prev r)
(if (>= 1 r) a (let* ([r-next (remainder r-prev r)]
[q (quotient r-prev r)]
[a-next (- a-prev (* q a))])
(iter a a-next r r-next)))
)
(let ([result (iter 0 1 n a)]) (if (< 0 result) result (+ n result)))
)
(define d (MultInverseModN e fi))При помощи алгоритма RSA можно шифровать сообщения, представленные серией чисел M в диапазоне от 0 до n-1. Шифрование состоит в возведении M в степень e в кольце вычетов по модулю n, дешифрование — в степень d. Благодаря тому, что умножение является ассоциативным, мы можем возводить в степень x за log(x) операций [7].
(define (PowerModN a b n)
(define (iter accumulator multiplicator power)
(if
(= power 0)
accumulator
(let
((new_accumulator (if (even? power) accumulator (remainder (* accumulator multiplicator) n))))
(iter new_accumulator (* multiplicator multiplicator) (quotient power 2))
)
)
)
(iter 1 a b)
)В моём примере открытый ключ представляет собой пару (250483 31), закрытый — пару (250483 32191). Зашифрованное сообщение 123456 равно 133240.
- en.wikipedia.org/wiki/RSA
- en.wikipedia.org/wiki/Integer_factorization
- en.wikipedia.org/wiki/Euler%27s_totient_function
- en.wikipedia.org/wiki/Euclidean_algorithm
- en.wikipedia.org/wiki/Modular_arithmetic
- en.wikipedia.org/wiki/Extended_Euclidean_algorithm
- en.wikipedia.org/wiki/Exponentiation_by_squaring
habr.com
Повышаем безопасность закрытых ssh-ключей / Habr
Вы когда-нибудь интересовались механизмом работы ssh-ключей? Или тем, насколько безопасно они хранятся?Я использую ssh каждый день много раз — когда запускаю git fetch или git push, когда развертываю код или логинюсь на сервере. Не так давно я осознал, что для меня ssh стал магией, которой я привык пользоваться без понимация принципов ее работы. Мне это не сильно понравилось — я люблю разбираться в инструментах, которые использую. Поэтому я провел небольшое исследование и делюсь с вами результатами.
По ходу изложения встретится много аббревиатур. Они не помогут понять идеи, но будут полезны в том случае, если вы решите погуглить подробности.
Итак, если вам доводилось прибегать к аутентификации по ключу, то у вас, скорее всего, есть файл ~/.ssh/id_rsa или ~/.ssh/id_dsa в домашнем каталоге. Это закрытый (он же приватный) RSA/DSA ключ, а ~/.ssh/id_rsa.pub или ~/.ssh/id_dsa.pub — открытый (он же публичный) ключ. На сервере, на котором вы хотите залогиниться, должна быть копия открытого ключа в ~/.ssh/authorized_keys. Когда вы пытаетесь залогиниться, ssh-клиент подтвержает, что у вас есть закрытый ключ, используя цифровую подпись; сервер проверяет, что подпись действительна и в ~/.ssh/authorized_keys есть открытый ключ, и вы получаете доступ.
Что же хранится внутри закрытого ключа?
Незашифрованный формат закрытого ключа
Закрытый ключ рекомендуется защищать паролем (парольной фразой), иначе злоумышленник, которому удалось украсть у вас закрытый ключ, сможет без проблем залогиниться на вашем сервере. Сначала взглянем на незашифрованный формат файла, а с зашифрованным разберемся позже.
Незашифрованный ключ выглядит примерно так:
-----BEGIN RSA PRIVATE KEY-----
MIIEogIBAAKCAQEArCQG213utzqE5YVjTVF5exGRCkE9OuM7LCp/FOuPdoHrFUXk
y2MQcwf29J3A4i8zxpES9RdSEU6iIEsow98wIi0x1/Lnfx6jG5Y0/iQsG1NRlNCC
aydGvGaC+PwwWiwYRc7PtBgV4KOAVXMZdMB5nFRaekQ1ksdH/360KCGgljPtzTNl
09e97QBwHFIZ3ea5Eih/HireTrRSnvF+ywmwuxX4ubDr0ZeSceuF2S5WLXh3+TV0
... и так далее ...
-----END RSA PRIVATE KEY-----
Закрытый ключ содержит данные в формате ASN.1, представленные в виде последовательности байт согласно стандарту X.690 и закодированные в Base64. Грубо говоря, ASN.1 можно сравнить с JSON (он поддерживает различные типы данных, такие как INTEGER, BOOLEAN, строки и последовательности, которые могут формировать древовидную структуру). ASN.1 широко распространен в криптографии, хотя слегка вышел из моды с пришествием веба (я не знаю почему — он выглядит как вполне достойный формат (с этим можно поспорить — прим. пер.))
Сгенерируем тестовый RSA-ключ без пароля, используя ssh-keygen, и декодируем его с помощью asn1parse (или воспользуемся написанным на JavaScript ASN.1-декодером):
$ ssh-keygen -t rsa -N '' -f test_rsa_key
$ openssl asn1parse -in test_rsa_key
0:d=0 hl=4 l=1189 cons: SEQUENCE
4:d=1 hl=2 l= 1 prim: INTEGER :00
7:d=1 hl=4 l= 257 prim: INTEGER :C36EB2429D429C7768AD9D879F98C...
268:d=1 hl=2 l= 3 prim: INTEGER :010001
273:d=1 hl=4 l= 257 prim: INTEGER :A27759F60AEA1F4D1D56878901E27...
534:d=1 hl=3 l= 129 prim: INTEGER :F9D23EF31A387694F03AD0D050265...
666:d=1 hl=3 l= 129 prim: INTEGER :C84415C26A468934F1037F99B6D14...
798:d=1 hl=3 l= 129 prim: INTEGER :D0ACED4635B5CA5FB896F88BB9177...
930:d=1 hl=3 l= 128 prim: INTEGER :511810DF9AFD590E11126397310A6...
1061:d=1 hl=3 l= 129 prim: INTEGER :E3A296AE14E7CAF32F7E493FDF474...
Структура данных в ASN.1 довольно проста: это последовательность из девяти целых чисел. Их назначение определено в RFC2313. Первое и третье числа — это номер версии (0) и открытая экспонента e. Второе и четвертое числа (длиной 2048 бит) — это модуль n и секретная экспонента d. Эти числа являются параметрами ключа RSA. Остальные пять можно получить, зная n и d — они кэшированы в файле для ускорения некоторых операций.
Структура DSA-ключей похожа и включает шесть чисел:
$ ssh-keygen -t dsa -N '' -f test_dsa_key
$ openssl asn1parse -in test_dsa_key
0:d=0 hl=4 l= 444 cons: SEQUENCE
4:d=1 hl=2 l= 1 prim: INTEGER :00
7:d=1 hl=3 l= 129 prim: INTEGER :E497DFBFB5610906D18BCFB4C3CCD...
139:d=1 hl=2 l= 21 prim: INTEGER :CF2478A96A941FB440C38A86F22CF...
162:d=1 hl=3 l= 129 prim: INTEGER :83218C0CA49BA8F11BE40EE1A7C72...
294:d=1 hl=3 l= 128 prim: INTEGER :16953EA4012988E914B466B9C37CB...
425:d=1 hl=2 l= 21 prim: INTEGER :89A356E922688EDEB1D388258C825...
Формат закрытого ключа, защищенного паролем
Теперь усложним жизнь потенциальному злоумышленнику, который смог украсть закрытый ключ — защитим его паролем. Что произошло с файлом?
$ ssh-keygen -t rsa -N 'super secret passphrase' -f test_rsa_key
$ cat test_rsa_key
-----BEGIN RSA PRIVATE KEY-----
Proc-Type: 4,ENCRYPTED
DEK-Info: AES-128-CBC,D54228DB5838E32589695E83A22595C7
3+Mz0A4wqbMuyzrvBIHx1HNc2ZUZU2cPPRagDc3M+rv+XnGJ6PpThbOeMawz4Cbu
lQX/Ahbx+UadJZOFrTx8aEWyZoI0ltBh9O5+ODov+vc25Hia3jtayE51McVWwSXg
wYeg2L6U7iZBk78yg+sIKFVijxiWnpA7W2dj2B9QV0X3ILQPxbU/cRAVTd7AVrKT
... и так далее ...
-----END RSA PRIVATE KEY-----
Заметим, что добавились две строки с заголовками, а результат декодирования Base64-строки больше не является валидным ASN.1. Дело в том, что структура ASN.1. зашифрована. Из заголовков узнаем, какой алгоритм использовался для шифрования: AES-128 в режиме CBC. 128-битная шестнадцатеричная строка в заголовке
DEK-Info — это вектор инициализации (IV). Ничего необычного здесь нет, все распространенные криптографические библиотеки умеют работать с используемыми здесь алгоритмами.Но как из пароля получается ключ AES? Я не нашел этого в документации и поэтому был вынужден разбираться в исходниках OpenSSL. Вот что я выяснил насчет получения ключа шифрования:
- Первые 8 байт вектора инициализации дописываются к паролю (по сути, являются солью).
- От полученной строки один раз берется MD5-хеш.
Для проверки расшифруем закрытый ключ, взяв вектор инициализации из заголовка
DEK-Info:$ tail -n +4 test_rsa_key | grep -v 'END ' | base64 -d |
openssl aes-128-cbc -d -iv D54228DB5838E32589695E83A22595C7 -K $(
ruby -rdigest/md5 -e 'puts Digest::MD5.hexdigest(["super secret passphrase",0xD5,0x42,0x28,0xDB,0x58,0x38,0xE3,0x25].pack("a*cccccccc"))'
) |
openssl asn1parse -inform DER
Эта команда выведет параметры ключа RSA. Если вы хотите просто увидеть ключ, есть способ и проще:
$ openssl rsa -text -in test_rsa_key -passin 'pass:super secret passphrase'
Но я хотел показать, как именно ключ AES получается из пароля, чтобы обратить внимание на два уязвимых места:
- Использование MD5 прописано в коде, а это значит, что без изменения формата невозможно перейти на другую хеш-функцию (например, SHA-1). Если выяснится, что MD5 недостаточно безопасен, будут проблемы. (На самом деле нет, см. комментарии — прим. пер.)
- Хеш-функция применяется только один раз. Так как MD5 и AES быстро вычисляемы, короткий пароль легко подобрать перебором.
Если ssh-ключ попадет в недобрые руки, например, кто-нибудь украдет ваш ноутбук или жеский диск с бэкапами, злоумышленник сможет перебрать большое количество паролей, даже обладая небольшой вычислительной мощностью. Если вы установили словарный пароль, его можно подобрать за секунды.
Это плохая новость: защита ключа паролем не так хороша, как можно было предположить. Но есть и хорошая новость: вы можете перейти на более надежный формат закрытого ключа.
Повышаем защиту ключа с использованием PKCS#8
Итак, нам нужен алгоритм получения симметричного ключа шифрования из пароля, который работал бы медленно, чтобы злоумышленнику потребовалось больше вычислительного времени для подбора пароля.
Для ssh-ключей существует несколько стандартов с неуклюжими названиями:
- В PKCS #5 (RFC 2898) определен алгоритм PBKDF2 (Password-Based Key Derivation Function 2) получения ключа шифрования из пароля путем многократного применения хеш-функции. Там же определена схема шифрования PBES2 (Password-Based Encryption Scheme 2), которая включает использование ключа, сгенерированного по PBKDF2, и симметричного шифра.
- В PKCS #8 (RFC 5208) определен формат хранения зашифрованных закрытых ключей с поддержкой PBKDF2. OpenSSL поддерживает закрытые ключи в формате PKCS#8, а OpenSSH использует OpenSSL, так что если вы пользуетесь OpenSSH, то можете переключиться с традиционного формата файлов ssh-ключей на формат PKCS#8.
Я не знаю, почему
ssh-keygen до сих пор генерирует ключи в традиционном формате, несмотря на то, что уже много лет существуют лучшие альтернативы. Дело не в совместимости с серверным софтом: закрытые ключи никогда не покидают пределы вашего компьютера. К счастью, существующие ключи достаточно легко преобразовать в формат PKCS#8:$ mv test_rsa_key test_rsa_key.old
$ openssl pkcs8 -topk8 -v2 des3 \
-in test_rsa_key.old -passin 'pass:super secret passphrase' \
-out test_rsa_key -passout 'pass:super secret passphrase'
Если попробовать использовать новый файл ключа в формате PKCS#8, можно обнаружить, что все работает так же как и раньше. Посмотрим, что теперь находится внутри файла.
$ cat test_rsa_key
-----BEGIN ENCRYPTED PRIVATE KEY-----
MIIFDjBABgkqhkiG9w0BBQ0wMzAbBgkqhkiG9w0BBQwwDgQIOu/S2/v547MCAggA
MBQGCCqGSIb3DQMHBAh5q+o4ELaHnwSCBMjA+ho9K816gN1h9MAof4stq0akPoO0
CNvXdtqLudIxBq0dNxX0AxvEW6exWxz45bUdLOjQ5miO6Bko0lFoNUrOeOo/Gq4H
dMyI7Ot1vL9UvZRqLNj51cj/7B/bmfa4msfJXeuFs8jMtDz9J19k6uuCLUGlJscP
... десу-десу ...
-----END ENCRYPTED PRIVATE KEY-----
Обратите внимание на то, что первая и последняя строки изменились (
BEGIN ENCRYPTED PRIVATE KEY вместо BEGIN RSA PRIVATE KEY), а заголовки Proc-Type и DEK-Info исчезли. Фактически, в файле хранятся данные во все том же формате ASN.1:$ openssl asn1parse -in test_rsa_key
0:d=0 hl=4 l=1294 cons: SEQUENCE
4:d=1 hl=2 l= 64 cons: SEQUENCE
6:d=2 hl=2 l= 9 prim: OBJECT :PBES2
17:d=2 hl=2 l= 51 cons: SEQUENCE
19:d=3 hl=2 l= 27 cons: SEQUENCE
21:d=4 hl=2 l= 9 prim: OBJECT :PBKDF2
32:d=4 hl=2 l= 14 cons: SEQUENCE
34:d=5 hl=2 l= 8 prim: OCTET STRING [HEX DUMP]:3AEFD2DBFBF9E3B3
44:d=5 hl=2 l= 2 prim: INTEGER :0800
48:d=3 hl=2 l= 20 cons: SEQUENCE
50:d=4 hl=2 l= 8 prim: OBJECT :des-ede3-cbc
60:d=4 hl=2 l= 8 prim: OCTET STRING [HEX DUMP]:78ABEA3810B6879F
70:d=1 hl=4 l=1224 prim: OCTET STRING [HEX DUMP]:C0FA1A3D2BCD7A80DD61F4C0287F8B2D...
Воспользуемся JavaScript-декодером, чтобы рассмотреть структуру ASN.1:
Sequence (2 elements)
|- Sequence (2 elements)
| |- Object identifier: 1.2.840.113549.1.5.13 // using PBES2 from PKCS#5
| `- Sequence (2 elements)
| |- Sequence (2 elements)
| | |- Object identifier: 1.2.840.113549.1.5.12 // using PBKDF2 — yay! :)
| | `- Sequence (2 elements)
| | |- Byte string (8 bytes): 3AEFD2DBFBF9E3B3 // salt
| | `- Integer: 2048 // iteration count
| `- Sequence (2 elements)
| Object identifier: 1.2.840.113549.3.7 // encrypted with Triple DES, CBC
| Byte string (8 bytes): 78ABEA3810B6879F // initialization vector
`- Byte string (1224 bytes): C0FA1A3D2BCD7A80DD61F4C0287F8B2DAB46A43E... // encrypted key blob
Здесь упоминаются OID (Object identifier) — глобально-уникальные цифровые идентификаторы. По ним мы узнаем, что используется схема шифрования pkcs5PBES2, функция получения ключа PBKDF2 и алгоритм шифрования des-ede3-cbc. Функция хеширования не указана явно, значит, по умолчанию используется hMAC-SHA1.
Хранение OID в файле хорошо тем, что ключи можно обновить без смены формата контейнера (если, например, будет изобретен лучший алгоритм шифрования).
Также мы видим, что в ходе получения ключа шифрования выполняется 2048 итераций. Это гораздо лучше, чем однократное применение хеш-функции при использовании традиционного формата ssh-ключей — перебор паролей потребует больше времени. В настоящий момент количество итераций прописано в коде OpenSSL, я надеюсь, в будущем его можно будет настраивать.
Заключение
Если вы установили сложный пароль на закрытый ключ, то преобразование его из традиционного формата в PKCS#8 можно сравнить с увеличением длины пароля на пару символов. Если же вы используете слабый пароль, PKCS#8 сделает его подбор заметно сложнее.
Поменять формат ключей очень просто:
$ mv ~/.ssh/id_rsa ~/.ssh/id_rsa.old
$ openssl pkcs8 -topk8 -v2 des3 -in ~/.ssh/id_rsa.old -out ~/.ssh/id_rsa
$ chmod 600 ~/.ssh/id_rsa
# проверьте, что новый ключ работает. если работает, старый можно удалить
$ rm ~/.ssh/id_rsa.old
Команда
openssl pkcs8 запрашивает пароль три раза: один раз для разблокировки существующего ключа и два раза при создании нового файла ключа. Вы можете придумать новый пароль или использовать старый, это не имеет никакого значения.Не весь софт может читать формат PKCS#8, но в этом нет ничего страшного — доступ к закрытому ssh-ключу нужен только ssh-клиенту. С точки зрения сервера, хранение закрытого ключа в другом формате вообще ничего не меняет.
Переводчик будет рад услышать замечания и конструктивную критику.
habr.com
RSA — шифрование online
Комментарий:
Описание: RSA (Rivest-Shamir-Adleman) является одной из первых криптосистем с открытым ключом и широко используется для безопасной передачи данных. В такой криптосистеме ключ шифрования является открытым и отличается от ключа расшифровки, который хранится в секрете (private). В RSA эта асимметрия основана на практической сложности факторизации произведения двух больших простых чисел, «проблема факторинга». Аббревиатура RSA состоит из начальных букв фамилий Рона Ривеста, Ади Шамира и Леонарда Адлемана, которые впервые публично описали алгоритм в 1978 году. Клиффорд Кокс, английский математик, работающий в Британском разведывательном управлении правительственной связи (GCHQ), разработал эквивалентную систему в 1973 году, но это не было рассекречено до 1997 года.
Пользователь RSA создает и затем публикует открытый ключ на основе двух больших простых чисел вместе с дополнительным значением. Простые числа должны храниться в секрете. Любой может использовать открытый ключ для шифрования сообщения, но с помощью опубликованных в данный момент методов, и если открытый ключ достаточно велик, только тот, кто знает простые числа, может расшифровать сообщение. Нарушение шифрования RSA известно как проблема RSA. Остается открытым вопрос, насколько это сложно, как проблема факторинга.
RSA является относительно медленным алгоритмом, и из-за этого он реже используется для прямого шифрования пользовательских данных. Чаще всего RSA передает зашифрованные общие ключи для шифрования с симметричным ключом, который, в свою очередь, может выполнять массовые операции шифрования-дешифрования на гораздо более высокой скорости.
Ресурсы:
crypt-online.ru
А что, если бы RSA ключи были бы не такими большими?
Всем привет! Прежде чем я начну, хочу поздравить от имени команды revers-pub всех кодеров с ДнЁм ПрОгРаММисТа! Всем добра!
Как-то я задумался, какую я выбрал бы себе сверхспособность, если бы поймал Гари Поттера и попросил бы его исполнить такое желание. На ум пришло сразу две вещи — проецирование радужных таблиц любого размера на жёсткий диск силой мысли и факторизация больших чисел в уме. Но это всё мечты. Сегодня я бы хотел поговорить о том, каким образом можно было бы «взломать» алгоритм RSA. Как мы знаем — его криптостойкость напрямую основана на том принципе, что по результату произведения двух простых чисел мы не можем догадаться какие при этом два сомножителя были использованы. Я не буду сейчас рассказывать принцип работы этого алгоритма, так как статья не об этом. Давайте представим себе следующую правдоподобную ситуацию: между двумя узлами сети была передана зашифрованная информация и открытый ключ. Попути, информация была перехвачена. Требуется расшифровать перехваченный файл. Чтобы это сделать, надо по открытому ключу, в котором передаётся публичная экспонента e и результат произведения p*q=N, получить закрытый. Как это сделать? Чтобы это сделать, нужно разложить на множители N, тем самым определив сомножители p и q. Когда я пытался разобраться со всем этим, в гугле нашёл хорошую статью, которая мне очень помогла. Хочу сразу уточнить то, что сертификаты бывают разных форматов — это DER формат, его чаще использует винда и PEM, его чаще всего используют никсы. Формат PEM создаётся по стандарту x.509. Отличия между ними на самом деле не существенные. В DER формате ключи пишутся в бинарном виде, а в PEM — в текстовом, закодированом в base64. Начало ключа обычно начинается с «——BEGIN RSA PRIVATE/PUBLIC KEY——». Мы будем использовать этот формат.
Чтобы смоделировать ситуацию максимально правдоподобно, давайте сконструируем сертификат с открытым ключом, зашифруем с его помощью наши данные и попробуем их потом расшифровать. Чтобы это сделать нужно сначала получить сертификат с секретными данными (закрытый ключ) по открытому. Приступим:
OpenSsl
Для создания сертификатов будем использовать специальную для этого тулзу — openssl. Она сама сгенерирует пары p и q, сосчитает все экспоненты и сконструирует сертификат. Итак, первым делом сгенерируем приватный ключ:
openssl genrsa -out priv.pem 256
Хочу заметить, что для теста, мы специально указываем число 256, чтобы N побыстрее разложилась на множители. В жизни чаще всего используется длина ключа — 2048 бит. После выполнения данной команды, openssl создаст нам секретный файл с закрытым ключом. Обычно его ещё тут же шифруют каким-нибудь симметричным алгоритмом, например, des. Чтобы это сделать сразу, можно было бы выполнить:
openssl genrsa -des3 -out priv.pem 256
Данная команда получит и зашифрует файл priv.pem. Перед шифрованием, программа запросит ввести ключ шифрования для алгоритма des.Файл priv.pem представляет из себя простой текстовой файл. В нём хранится открытый и закрытый ключ. В моём случае его содержание получилось таким:
-----BEGIN RSA PRIVATE KEY----- MIGsAgEAAiEAqnP8R6UcdQX7YMe2oZg211LIhdb9vQ6akBpeCYg+AV8CAwEAAQIh AKk5DTVzzpS/o5mprL8xhv8P4Yi4yeFNMky3WHWbq7rBAhEA1iTtWAlurhKfUZH9 4y3UbQIRAMvE5Uo4efnXAKRjvmJ8FXsCEQCgt4IyCpI4rt1HeQxVDjZZAhEApwsB IIgNzjdn6ltuLlQkUwIQEypbq/MV2u7cNQGXTvXqIw== -----END RSA PRIVATE KEY-----
Вторым шагом будет -экспорт публичного ключа из файла priv.pem. Как раз эту информацию мы и будем передавать вместе с зашифрованными данными.
openssl rsa -in priv.pem -outform PEM -pubout -out pub.pem
У меня файл pub.pem получился таким:
-----BEGIN PUBLIC KEY----- MDwwDQYJKoZIhvcNAQEBBQADKwAwKAIhAKpz/EelHHUF+2DHtqGYNtdSyIXW/b0O mpAaXgmIPgFfAgMBAAE= -----END PUBLIC KEY-----
Просмотреть подробную информацию о ключах вы можете так:
О секретном:
openssl rsa -in priv.pem -text -noout
У меня вот что получилось:
Private-Key: (256 bit)
modulus:
00:aa:73:fc:47:a5:1c:75:05:fb:60:c7:b6:a1:98:
36:d7:52:c8:85:d6:fd:bd:0e:9a:90:1a:5e:09:88:
3e:01:5f
publicExponent: 65537 (0x10001)
privateExponent:
00:a9:39:0d:35:73:ce:94:bf:a3:99:a9:ac:bf:31:
86:ff:0f:e1:88:b8:c9:e1:4d:32:4c:b7:58:75:9b:
ab:ba:c1
prime1:
00:d6:24:ed:58:09:6e:ae:12:9f:51:91:fd:e3:2d:
d4:6d
prime2:
00:cb:c4:e5:4a:38:79:f9:d7:00:a4:63:be:62:7c:
15:7b
exponent1:
00:a0:b7:82:32:0a:92:38:ae:dd:47:79:0c:55:0e:
36:59
exponent2:
00:a7:0b:01:20:88:0d:ce:37:67:ea:5b:6e:2e:54:
24:53
coefficient:
13:2a:5b:ab:f3:15:da:ee:dc:35:01:97:4e:f5:ea:
23
О публичном:
openssl rsa -noout -text -inform PEM -in pub.pem -pubin или сразу убрать двоеточия между байтами openssl rsa -noout -text -inform PEM -in pub.pem -pubin | sed -e 's/://g' | tr 'a-z' 'A-Z'
1 вариант:
Public-Key: (256 bit)
Modulus:
00:aa:73:fc:47:a5:1c:75:05:fb:60:c7:b6:a1:98:
36:d7:52:c8:85:d6:fd:bd:0e:9a:90:1a:5e:09:88:
3e:01:5f
Exponent: 65537 (0x10001)
2 вариант:
PUBLIC-KEY (256 BIT)
MODULUS
00AA73FC47A51C7505FB60C7B6A198
36D752C885D6FDBD0E9A901A5E0988
3E015F
EXPONENT 65537 (0X10001)
Всё, сертификаты готовы, осталось их применить и зашифровать какие-нибудь данные. Я создал файл file.txt с текстом «reverse-pub.ru».
Шифруем его открытым ключом:
openssl rsautl -encrypt -inkey pub.pem -pubin -in enc.txt -out file.ssl
Файл зашифровался и превратился в абсолютно нечитабельный вид:
Зашифрованный файл
Итак, допустим, в результате перехвата нам достался вот этот зашифрованный файл — file.ssl и файл открытого ключа. Попробуем восстановить по нему файл секретного ключа — private.pub.
Для этого нам нужно факторизовать число N. Это можно сделать с помощью утилиты yafu. Её мне посоветовал один классный вирусный аналитик, за что ему огромное спасибо! Итак, запускаем тулзу и пишем команду factor(N), где вместо N подставляем модуль- число, представляющее из себя произведение p и q. Оно берётся из открытого ключа.
factor(0xAA73FC47A51C7505FB60C7B6A19836D752C885D6FDBD0E9A901A5E09883E015F)

Факторизация модуля N с помощью yafu
Теперь остаётся ждать, пока числа факторизуются. Если бы N было бы размером в 2048 бит, то ждать бы пришлось и нашим внукам. Но у нас длина ключа маленькая и результат не заставляет себя так долго ждать! Смотрите, тулза факторизовала число N!
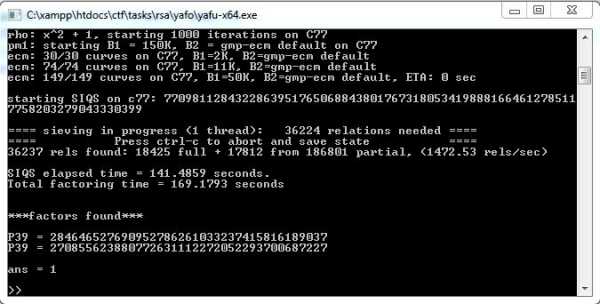
Результат работы yafu
У нас есть числа p и q! Это 284646527690952786261033237415816189037 и 270855623880772631112272052293700687227!
Самое сложное позади, осталось теперь на основании этих данных сгенерировать файл закрытого ключа. Для этого я написал простенький скрипт на python, который получает закрытый ключ d по открытому {e,N}. В него нужно вставить только значения p и q и он нам создаст файл private.cer. Исходный код скрипта такой:
# -*- coding: utf-8 -*-
# d = (k*f(n) +1) / e
# надо подобрать k так, чтобы результат деления был целым. Если не так, то инкрементируем k.
# Есть много разных k, при которых это условие выполнится. Причём, при валидных k ключ d может
# быть разный, но всё-равно валидный....
# функция Эйлера
# p и q находятся методом факторизации n - module
def getFn(p, q):
return (p-1)*(q-1)
# e - публичная экспонента
# Fn - F(n)
def get_k(e, Fn):
k = 1
while True:
if (k*Fn+1) % e == 0:
return k
k=k+1
# p*q = n
# Fn - функция Эйлера.
def get_d(k,Fn,e):
return (k*Fn+1) / e
#
# из публичного ключа берём e
# из публичного ключа берём module и факторизируем его, получаю p и q
#
#
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, x, y = egcd(b % a, a)
return (g, y - (b // a) * x, x)
# x = mulinv(b) mod n, (x * b) % n == 1
def mulinv(b, n):
g, x, _ = egcd(b, n)
print(g,x,_)
if g == 1:
return x % n
#Создаёт файл приватного ключа
def makePkey(fileName, n, e, d, p, q, e1, e2, coof):
fileContent = '''asn1=SEQUENCE:rsa_key\n
[rsa_key]
version=INTEGER:%d
modulus=INTEGER:%d
pubExp=INTEGER:%d
privExp=INTEGER:%d
p=INTEGER:%d
q=INTEGER:%d
e1=INTEGER:%d
e2=INTEGER:%d
coeff=INTEGER:%d ''' % (0, n, e, d, p, q, e1, e2, coof)
f = open(fileName,'w')
f.write(fileContent)
f.close()
###############################################################
###################### MAIN ###################################
###############################################################
######## Меняем на своё ############
# p &gt; q
p = 284646527690952786261033237415816189037
q = 270855623880772631112272052293700687227
e = 65537
#p = 53
#q = 59
#e = 3
############################################################
n = p*q;
Fn = getFn(p, q)
k = get_k(e, Fn)
d = get_d(k, Fn, e)
#d = mulinv(e, Fn) !работает!
print "Public Key {e, n}: {%d, %d} {0x%X, 0x%X}" % (e, n, e, n)
print "Privet Key {d, n}: {%d, %d} {0x%X, 0x%X}" % (d, n, d, n)
#check
exampl = 123456789
enc = pow(exampl, e, n)
print "exampl orig %d, exampl enc %d " % (exampl, enc)
dec = pow(enc, d, n)
print "exampl orig %d, exampl dec %d " % (exampl, dec)
############################## Для восстановления privet key ##############
e1 = d % (p-1)
e2 = d % (q-1)
coof = mulinv(q, p)
print "e1: %d: 0x%x" % (e1, e1)
print "e2: %d: 0x%x" % (e2, e2)
print "coof: %d: 0x%x" % (coof, coof)
makePkey("private.txt", n, e, d, p, q, e1, e2, coof)
Скрипт нам сгенерил файл private.txt. У меня он получился таким:
asn1=SEQUENCE:rsa_key [rsa_key] version=INTEGER:0 modulus=INTEGER:77098112843228639517650688438017673180534198881664612785117758203279043330399 pubExp=INTEGER:65537 privExp=INTEGER:76541672857039965234545743511774751480570272121805447666126387908639206390465 p=INTEGER:284646527690952786261033237415816189037 q=INTEGER:270855623880772631112272052293700687227 e1=INTEGER:213629310328626634497080745464918062681 e2=INTEGER:222038213421342289187891054053116093523 coeff=INTEGER:25475267710492865297665627336843061795
Теперь нужно скормить эти данные openssl, чтобы она нам из них сделала файл сертификата.
Выполняем:
openssl asn1parse -genconf private.txt -out private.cer
Тулза нам сгенерит сертификат в DER формате. Прежде чем мы его переконвертируем в x.509, давайте проверим его на валидность. Делается это так:
openssl rsa -in private.cer -inform der -text -check
Вот что выдала тулза:
Private-Key: (256 bit)
modulus:
00:aa:73:fc:47:a5:1c:75:05:fb:60:c7:b6:a1:98:
36:d7:52:c8:85:d6:fd:bd:0e:9a:90:1a:5e:09:88:
3e:01:5f
publicExponent: 65537 (0x10001)
privateExponent:
00:a9:39:0d:35:73:ce:94:bf:a3:99:a9:ac:bf:31:
86:ff:0f:e1:88:b8:c9:e1:4d:32:4c:b7:58:75:9b:
ab:ba:c1
prime1:
00:d6:24:ed:58:09:6e:ae:12:9f:51:91:fd:e3:2d:
d4:6d
prime2:
00:cb:c4:e5:4a:38:79:f9:d7:00:a4:63:be:62:7c:
15:7b
exponent1:
00:a0:b7:82:32:0a:92:38:ae:dd:47:79:0c:55:0e:
36:59
exponent2:
00:a7:0b:01:20:88:0d:ce:37:67:ea:5b:6e:2e:54:
24:53
coefficient:
13:2a:5b:ab:f3:15:da:ee:dc:35:01:97:4e:f5:ea:
23
RSA key ok
-----BEGIN RSA PRIVATE KEY-----
MIGsAgEAAiEAqnP8R6UcdQX7YMe2oZg211LIhdb9vQ6akBpeCYg+AV8CAwEAAQIh
AKk5DTVzzpS/o5mprL8xhv8P4Yi4yeFNMky3WHWbq7rBAhEA1iTtWAlurhKfUZH9
4y3UbQIRAMvE5Uo4efnXAKRjvmJ8FXsCEQCgt4IyCpI4rt1HeQxVDjZZAhEApwsB
IIgNzjdn6ltuLlQkUwIQEypbq/MV2u7cNQGXTvXqIw==
-----END RSA PRIVATE KEY-----
Самое главное, чтобы в конце мы нашли строке RSA key ok. У нас всё окей, так что двигаемся дальше. Конвертируем его в PEM формат:
openssl rsa -inform DER -outform PEM -in private.cer -out private.pem
Дальше можно проверить и этот файл, но это совсем не обязательно. Если очень хочется, то можно сделать это так:
openssl rsa -in private.pem -inform PEM -text -check
Убедившись, что всё в порядке, давайте теперь расшифруем с помощью полученного нами private.pem файл file.ssl.
openssl rsa -in private.pem -inform PEM -text -check openssl rsautl -decrypt -inkey private.pem -in file.ssl -out decrypt.txt
В итоге имеем расшифрованный файл decrypt.txt:
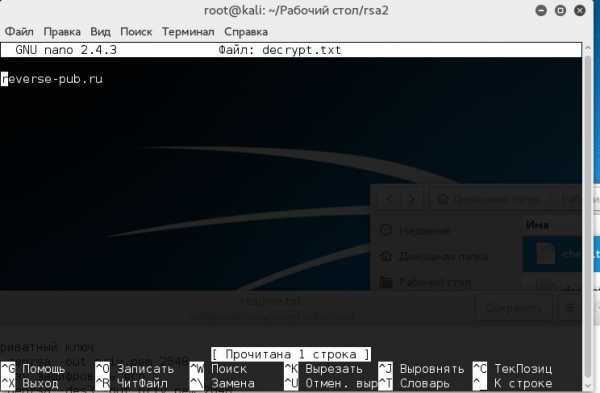
Результат
Думаю, теперь вы на практике убедились, что использование коротких ключей может привести к плачевным результатам.
If you found an error, highlight it and press Shift + Enter or click here to inform us.
reverse-pub.ru
Создание RSA ключей для доступа на сервер и обеспечения безопасности SSH
Как создать RSA ключи для доступа на сервер и как обезопасить SSH соединение с помощью публичного ключа — именно такими вопросами задаются многие люди, которым приходится работать удаленно с крупными проектами. Действительно, доступ на сервер с помощью ключа RSA — это удобно и полезно с точки зрения безопасности.
Недавно и я столкнулся с такой проблемой, а так как опыта работы в Linux у меня не очень много, то поиск толкового гайда отнял больше времени, чем я думал. Поэтому хочу поделиться полученным опытом и подробно описать шаги для новичков.
Сперва теория. Что нам для этого нужно? Во-первых, создать пару специальных криптографических ключей — открытый и закрытый. (Подробнее об алгоритме RSA можете почитать в Педивикии). Внести изменения в файл настроек сервиса SSH в Ubunt’e для того, чтобы указать, где искать сам ключ и для того, чтобы запретить авторизацию по паролю (если это нужно).
Список необходимых программ:
- WinSCP
- PuTTY
- PuTTYgen
- Pageant
Их все можно скачать со странички разработчика.
Итак, порядок действий.
1. Коннектимся на удаленный сервак с помощью PuTTY.
2. Переходим в директорию /.ssh/. Для этого выполняем команду
cd ~/.ssh/
3. Собственно, создаем сами ключи. Для этого выполняем:
ssh-keygen -t rsa
После выполнения этой команды увидите следующее
Generating public/private rsa key pair.
Enter file in which to save the key (/root/.ssh/id_rsa):#нажимаем [ENTER], если хотим оставить созданные ключи в папке /.ssh/
Enter passphrase (empty for no passphrase):
#вводим пароль (или, если не хотите защищать ключи паролем, не вводим и оставляем пустым) и нажимаем [ENTER]
Enter same passphrase again:
#повторяем пароль и опять [ENTER]
Your identification has been saved in /root/.ssh/id_rsa.
Your public key has been saved in /root/.ssh/id_rsa.pub.
The key fingerprint is:
2f:33:f6:f7:3f:13:4c:1f:04:9а:18:fa:0d:b2:а4:35 root@Ubuntu-1004-lucid-64-minima
Последние 4-ре строки описывают расположение ключей и рассказывают о нашем fingerprint’e. Это последовательность символов, используемая для аутентификации или поиска более длинного ключа. Подробнее здесь.
И, да. Сам ключ готов и сохранен в директории /.ssh/. Его графическое отображение выглядит так:
4. После того, как ключ готов, необходимо сделать его копию в новый файл. Для этого выполним команду:
at id_rsa.pub >> authorized_keys
Вместо «authorized_keys» можно ввести любое другое имя файла. Просто в конфигах SSH уже есть закомментированная строчка с указанием именно этого названия.
5. Теперь необходимо выставить правильные права доступа:
chmod -R 600 * #чтение и запись только для владельца
chmod 700 ~/.ssh/ #чтение, запись и исполнение только для владельца
6. С помощью WinSCP нужно стянуть файлик id_rsa (не оставляя копии на сервере) к себе на компьютер.
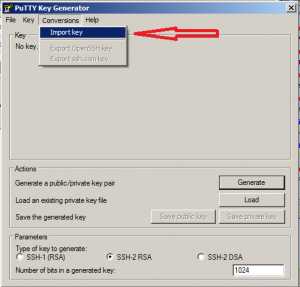
7. Теперь нам пригодятся остальные программы. Нам нужно преобразовать этот ключ в ключ, который понимает PuTTY и WinSCP. Для этого берем ранее скачанную программу PuTTYgen. В пункте меню «Conversions» выбираем «Import key». Далее указываем путь к слитому в 6-м пункте файлику. PuTTYgen спросит нас про пароль (если указывали — укажите и сейчас). И сохраняем новый ключ, нажав на кнопку «Save private key»
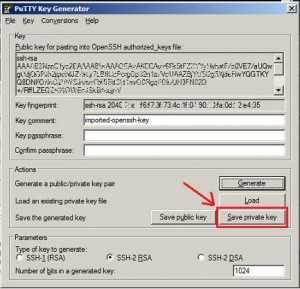
8. Теперь нужно поправить конфиги SSH на сервере. Для этого нужно открыть файл /etc/ssh/sshd_config. Я советую для этого использовать Midnight Commander (в Ubuntu устанавливается apt-get install mc. Открывается просто mc). Идем по указанному адресу, открываем на редактирование конфиг и ищем там следующие строки:
PermitRootLogin yes
(Если будете заходить на сервер под учетной записью root)
RSAAuthentication yes
PubkeyAuthentication yes
AuthorizedKeysFile .ssh/authorized_keys
PermitEmptyPasswords no
PasswordAuthentication no
UsePAM no
Значения должны быть такими, как сказано выше.
9. После сохранения отредактированного конфига нужно перезапустить службу SSH (если не уверены в своих действиях, вспомните примету:»Перезапуск SSH — к поездкам» 🙂 ). Для этого выполняем команду:
service ssh restart
10. Теперь открываем Pageant и добавляем созданный на шаге 7 ключ *.ppk.
11. PROFIT!!!1 Теперь, если все было сделано правильно, PuTTY или WinSCP не будут требовать пароль. В дальнейшем не забывайте подгружать Pageant с ключом RSA. И не забудьте сохранить сам ключ в надежном месте 🙂
P.S. если статья была вам полезна, не поленитесь, оставьте, пожалуйста, коммент 🙂 Спасибо.
kimonniez.ru
