Ethereum Classic ETC График сложности сети
Сервер статистики временно недоступен. Это не влияет на процесс майнинга. Майнинг идёт в штатном режиме.
Что такое сложность Ethereum Classic?Под сложностью Ethereum Classic подразумевается сложность добычи этой криптовалюты. Сложность Ethereum Classic называют также сложностью сети Ethereum Classic. Это основной параметр сети, который показывает сколько работы в среднем должно проделать майнинг-оборудование, чтобы найти блок. Чем больше майнеров в сети криптовалюты, тем выше сложность ее добычи, т.е. тем сложнее задача, которую должны решить майнеры для нахождения блока. Что такое майнинг?В чем измеряется сложность сети?Сложность сети показывает сколько раз в среднем майнеры должны вычислить значение hash-функции, чтобы найти криптовалютный блок.- 1 K = 1 000
- 1 M = 1 000 K = 1 000 000
- 1 G = 1 000 M = 1 000 000 K = 1 000 000 000
- 1 T = 1 000 G = 1 000 000 M = 1 000 000 000 K = 1 000 000 000 000

Сложность сети
Биткоин, Лайткоин, Эфириум Сложность Майнинга график
Биткоин, Лайткоин, Эфириум Сложность Майнинга графикСредняя сложность майнинга в день
btc eth xrp ltc zec dash bch doge bsv etc xmr btg rdd vtc blk ftc
Число уникальных транзакций в деньСредний размер блокаЧисло уникальных исходящих адресов в деньСредняя сложность майнинга в деньСредний хешрейт (hash/s) в деньСредняя цена, USD, в день, USDПрибыльность Майнинга USD/День за 1 Hash/sОтправлено коинов в деньСредняя комиссия за транзакцию, USDМедиана комиссии за транзакцию, USDСреднее время блока (время нахождения) (минуты)Рыночная капитализация, USDСредняя сумма транзакции, USDМедиана суммы транзакции, USDТвитов в деньGoogle Trends to «Bitcoin» @ 2012-01-01Число активных (вход. или вых.) адресов в деньТоп 100 богатейших адресов к весго монет %Средний Процент Комисии в Общем Вознагражении за блокCompare with…Число уникальных транзакций в деньСредний размер блокаЧисло уникальных исходящих адресов в деньСредняя сложность майнинга в деньСредний хешрейт (hash/s) в деньСредняя цена, USD, в день, USDПрибыльность Майнинга USD/День за 1 Hash/sОтправлено коинов в деньСредняя комиссия за транзакцию, USDМедиана комиссии за транзакцию, USDСреднее время блока (время нахождения) (минуты)Рыночная капитализация, USDСредняя сумма транзакции, USDМедиана суммы транзакции, USDТвитов в деньGoogle Trends to «Bitcoin» @ 2012-01-01Число активных (вход. или вых.) адресов в деньТоп 100 богатейших адресов к весго монет %Средний Процент Комисии в Общем Вознагражении за блок
или вых.) адресов в деньТоп 100 богатейших адресов к весго монет %Средний Процент Комисии в Общем Вознагражении за блокCompare with…Число уникальных транзакций в деньСредний размер блокаЧисло уникальных исходящих адресов в деньСредняя сложность майнинга в деньСредний хешрейт (hash/s) в деньСредняя цена, USD, в день, USDПрибыльность Майнинга USD/День за 1 Hash/sОтправлено коинов в деньСредняя комиссия за транзакцию, USDМедиана комиссии за транзакцию, USDСреднее время блока (время нахождения) (минуты)Рыночная капитализация, USDСредняя сумма транзакции, USDМедиана суммы транзакции, USDТвитов в деньGoogle Trends to «Bitcoin» @ 2012-01-01Число активных (вход. или вых.) адресов в деньТоп 100 богатейших адресов к весго монет %Средний Процент Комисии в Общем Вознагражении за блок
График сложности ethereum classic — Ethereum
04.04.2021
На нашем сайте представлен Курс Ethereum Classic и график его изменения, позволяющий в динамике увидеть, как меняются котировки по отношению к доллару, евро. Смотрите курс эфириум классик к доллару США (ETC/USD) на онлайн графике, в любое удобное для Вас время. Ethereum Classic Labs выступила против платформ по аренде мощностей хэширования — dia | Bits | 5 месяцев назад: Сеть Ethereum Classic подверглась атаке 51% — уже третий раз за месяц — Bloomchain | Bloomchain | 5 месяцев назад. График сложности майнинга в сети Ethereum Classic (по данным coinwarz) (хорошо видно падение сложности с 27 сентября, вызванное массовым отвалом 4 Гб карт):. 18 В видео Биткоин. Ethereum Classic is an open source, blockchain-based distributed computing platform featuring smart contract (scripting) functionality. Прогноз цены на март года. Цена ETH упала с $14 до $10 ввиду скандала с DAO. Капитализация. График курса Ethereum Classic за последние полгода, график роста. Scan the QR code or copy the address below into your wallet to send some Bitcoin. График цены Ethereum Classic (ETC) После хардфорка года цена ETC составляла всего 60-70 центов.
Ethereum Classic (ETC) Добавить в список наблюдения. Ознакомьтесь с текущим биржевым курсом пары Ethereum Classic/Биткоин, а также узнайте годовую историю его изменения и краткосрочный прогноз. Этот график, по. На сайте представлен конвертер валют и курс ETC к другим мировым валютам. Далее с января изменение сложности начало стремительно расти, и уже летом это значение достигло отметки 250 терахеш. Информация о криптовалюте Ethereum Classic Ethereum Classic (ETC) цена, график, капитализация, сложность сети — WikiMiner Analytics Вход или Регистрация.
Самые выгодные и надежные автоматические обменники Интернета, производящие обмен по направлению. Партнеры. Платформа использует технологию блокчейн для хранения реестра операций и данных. Сложность Ethereum Classic называют также сложностью сети Ethereum Classic.
Разница между Ethereum Classic и Ethereum заключается еще в одном важном параметре — капитализации. Будьте бдительны, рынок всегда даёт 2-ой шанс для хорошего входа. На примере отключены графики хешрейта сети и сложности, но оставлен график награды за блок в сети Ethereum. Биткоин рос с 25 марта, но вчера ралли остановилось, а на графиках появилась свеча Доджи Долгосрочный тренд по главной криптовалюте сохраняет бычью. Платформы во многом похожи, но имеют и ряд существенных различий. График сложности ethereum classic
Онлайн-график Ethereum Classic / TetherUS — не упустите ни одного изменения цены. Ethereum Classic График цен сегодня — Live ETC / Ethereum Classic (ETC) на,,,, | Елена | StormGain_crypto | Декабрь, Объяснение денежно-кредитной политики Ethereum Classic — Etherplan.
Ethereum Classic Курс, график, рыночная капитализация, команда, новости, динамика, курс etc к доллару, курс к рублю, вся информация на сегодня и многое другое. Онлайн-курс эфириум классика. За год график Ethereum Classic показал восемь заметных трендов: 📉 Нисходящий тренд с 6 января по 6 февраля: цена упала с 5,50 до 3,76 USD. 3 мес. 59, рыночная капитализация равна $ 1.
Сложность сети ethereum. Ethereum Classic хардфорк Thanos: майнинг и смена алгоритма. Хардфорк 2 января года. Вы можете посмотреть онлайн график сложности Ethereum здесь. График сложности ethereum classic
ICO статистика. Взгляните на график изменения сложности добычи монеты. Команда Ethereum classic (ETC) проведет форк в ближайшие дни как часть заявки на диффузию так называемой «бомбы» в коде сети. USD 11,32. Также в списке есть Ethereum Classic и Ethereum. Самые надежные и выгодные обменники, осуществляющие обмен Ethereum Classic на Mir RUR.
Текущий курс Ethereum Classic цены к доллару США — $ 12. График цены, объем торгов, рыночная капитализация и многое другое. В данной статье мы сделаем полный обзор etc криптовалюта. Стоимость Ethereum classic в USD, графики, самые популярные криптовалюты, как продавать и покупать ETC. Ethereum Classic прошел технический хард-форк, чтобы скорректировать внутренние цены для различных опкодов Виртуальной Машины Эфириума (EVM) 25 октября, аналогично хард-форку, совершенному Ethereum. Это основной параметр сети, который показывает сколько работы в среднем должно проделать майнинг-оборудование, чтобы найти блок.
Курс Ethereum Classic (ETC) в EUR, USD и рублях. График сложности ethereum classic
График сложности ethereum classic
- Криптовалюта Ethereum Classic: онлайн-график курсов, котировки
- Курс Ethereum Classic (ETC) к рублю на сегодня — онлайн
- Ethereum Classic (ETC) цена, график, капитализация, сложность
- Ethereum-classic (ETC) — Курс, График +Полный обзор
- Ethereum Classic предоставляет новые возможности
- Ethereum Difficulty Chart — CoinWarz
- Ethereum Classic Price | ETC Price Index and Live Chart
- Ethereum Classic Эфириум Классик (ETC) курс, цена, графики
- Ethereum Classic — курс в рублях и usd, новости ETC, график цен
- Ethereum — Все статьи и актуальная информация
График сложности сети ethereum classic
03.04.2021
И, если вы майнер, можете подумать, что лучше поддерживать Ethereum PoW». ) адресов в день) 18,395. 3 Регистрация. При этом его главной задачей стала ликвидация «бомбы сложности». В течение марта продолжалось постепенное снижение к 1715 TH, но за апрель случилось повторное возвращение к 1900 TH. Ethereum Classic(ETC) курс к рублю и usd. Курс Ethereum Classic и график на сегодня Среди прочих криптовалют Ethereum Classic держится особняком. 376 долл США, минимальный курс ETC/USD был 3. Ethereum (ETH) — калькулятор расчета доходности майнинга эфириума в реальном времени. Помешать хакерам вывести деньги должен был хардфорк сети Эфириума, но. Последние новости о коронавирусе в Коле на года. Хешрейт сети. Ethereum PoS, Ethereum PoW. Сеть Ethereum Classic готовит форк для окончательного устранения «бомбы сложности». Связь сложности и хешрейта сети.
Ethereum Classic (ETC) — это блокчейн-платформа, которая является продолжением сети Ethereum. Команда Ethereum classic (ETC) проведет форк в ближайшие дни как часть заявки на диффузию так называемой «бомбы» в коде сети. График динамики курса Ethereum Classic/USD онлайн Ключевые показатели криптовалюты Ethereum Classic Максимальная стоимость Ethereum Classic за 52 недели 16.
Сложность заключается в числе, которое регулирует время, необходимое майнерам для извлечения следующего блока, который затем будет добавлен в блокчейн. ETC сложность сети периодически корректируется в зависимости от среднего времени нахождения блока. TheDAO – венчурный фонд, основанный разработчиками платформы Ethereum, который два года назад привлек 168 млн. 35 Th/s-6. График развития.
Весна — Ethereum Classic отложил «бомбу сложности» в своей сети. Сеть Ethereum Classic получила обновление,. Ethereum Classic предоставляет валюту «Эфир» (Классический Эфир, Classic Ether, ETC), который может передаваться от одного участника сети другому и используется для оплаты вычислений, производимых. Что такое сложность майнинга Эфириума История и график сложности Ethereum. ☺ Актуальный курс Ethereum к доллару, евро, рублю. График сложности сети ethereum classic
Иногда сложность обозначают в P/T/G или Ph/Th/Gh. График. Ethereum Classic калькулятор доходности. На момент написания этой статьи у Ethereum Classic было 252 клиента Parity Ethereum, 167 Geth Classic, 80 Multi-Geth и 1 Besu на 500 клиентов.
Давайте разберемся,. Более того, графики рассчитываются и на будущее. 2 Что такое число вычислений Ethereum? Особенности. График роста сложности сети Ethereum. Проект в первую очередь направлен на реализацию канонических принципов цифровых денег. График сложности сети ethereum classic
616 GB, поэтому данную криптовалюту могут майнить только видеокарты с памятью более 3 GB. Вы сможете узнать о том, что такое криптовалюта Эфириум Классик, актуальный курс etc и увидеть график etc. Рентабельность добычи, «Бомба сложности» и ее использование.
«Бомба сложности» была задумана как механизм затруднения майнинга и предназначена для того, чтобы сделать его невозможным и абсолютно. Coinbase объявила через официальный аккаунт, что они работают над технической частью добавления Ethereum Classic на свою площадку и это. Обсуждение перспектив. Какие факторы влияют на данный показатель. Последние новости о коронавирусе в Стерлитамаке на года. График сложности сети ethereum classic
Типа ethereum classic. В среднем это время составляет десять минут для Биткоина. Где посмотреть график сложности майнинга Ethereum, Bitcoin и других криптовалют: сайты, калькуляторы. Онлайн графика сложности добычи криптовалюты Эфириум за все время. Награда за блок. График сложности сети ethereum classic
2 Личный кабинет; 3. График сложности сети ethereum classic
- Ethereum Classic — Википедия
- Сложность майнинга сети Ethereum и график роста
- Сложность сети Ethereum — онлайн график майнинга ETH
- Ethereum Classic ETC График хешрейта сети — 2Miners
- Сложность сети Ethereum Classic поднялась после объявления от
- График сложности Bitcoin — Blockchair
- Цена Эфириум Классик, ценовой индекс, график и информация о
- График сложности добычи криптовалют
- О возможных изменениях в алгоритме майнинга Ethereum Classic
- Ethereum Classic ETC криптовалюта: Курс, Кошелек, Майнинг
Мощность сети Эфириум: график, факторы влияния
Мощность сети Эфира (EThereum) — показатель, влияющий на сложность монеты, связан с популярностью токена у майнеров. Чем система мощнее, тем сложнее добывать блоки.
Содержание статьи:
Что это такое
Blockchain Ethereum пока работает на алгоритме Proof-of-Work, хотя в скором времени планируется переход на Proof-of-Stake. Все PoW-системы основаны на принципе изменения сложности. Сложность влияет на то, как долго майнеры ищут заветный хеш (ключ, приводящий к созданию блока).
Все PoW-системы основаны на принципе изменения сложности. Сложность влияет на то, как долго майнеры ищут заветный хеш (ключ, приводящий к созданию блока).
График мощности сети ETH отслеживает изменения показателя. Сложность меняется в большую или меньшую сторону, чтобы скорость формирования блока всегда оставалась примерно одинаковой.
Недавно мощность Эфириума была в очередной раз увеличена. Причина — грядущий переход на PoS, когда майнинг уже не нужен, а прибыль зависит от количества монет на балансе конкретного пользователя. Разработчики вводят все новое постепенно, в 3–4 этапа. Многим майнерам такое решение кажется неблагоприятным, что чревато образованием хардфорка, как это случилось в 2016 году (тогда появились монеты Эфириум Классик).
Какие факторы влияют
Мощность Эфира определяется рядом технических и экономических факторов:
- Длительность формирования блока. В системе ETH среднее время нахождения хеша равно 14–15 секундам. Если параметр заметно снижается, сложность автоматически увеличивается и наоборот. Схема гарантирует равновесие блокчейн-системы.
- Новые технологии. Майнинг Ethereum с помощью видеокарт становится все менее доходным делом. На смену приходят ASIC-майнеры, что провоцирует стремительный рост сложности.
- Рост стоимости монеты. Чем выше курс Эфириума к доллару, тем валюта популярнее. Это приводит к увеличению числа майнеров и, как следствие, усложнению процесса.
- Расценки на электрическую энергию. Мощность сети Эфириум, как показывают графики, растет, требуя высокомощного оборудования. Техника потребляет много электричества, добавляя заметную статью расходов для майнеров.
- Рентабельность, окупаемость. Фактор относится к косвенным — чем выгоднее криптоэнтузистам добывать Эфир, тем большим будет количество майнеров. Последствие очевидно: увеличение сложности и требуемых параметров устройств для нахождения хеша.

Конкретизируя, параметр рассчитывается на основе двух факторов: времени генерации блока и суммарной мощности сети (общий хешрейт всех устройств в составе системы).
График мощности
Мощность Эфириума важна для майнеров, трейдеров, инвесторов. Все желающие получить прибыль с криптовалюты держат под контролем показатель. Сайты, предоставляющие графики мощности сети Эфириум с регулярным обновлением:
- Cryptorate.ru;
- Coinwarz.com;
- Bitinfocharts.com.
Последний отличается наибольшей наглядностью. Выдает информацию за любой период, начиная с момента создания 1 Эфириума, размер вознаграждения, позволяет сравнить параметр Ethereum с аналогичным у других криптовалют.
Сведения на разных сайтах могут незначительно различаться. Показатель анализируется и корректируется часто, а период обновления у разных ресурсов собственный. Рекомендуется брать информацию из нескольких источников, а затем рассчитывать среднее арифметическое. Еще точнее будут сведения не за последние 1 или 2 дня, а за 2–3 месяца.
В оставшийся недолгий промежуток времени до внедрения PoS Ethereum считается выгодным криптовалютным активом. Дальнейшие события зависят от действий разработчиков.
Ethereum сложность — Ethereum Difficulty Chart
02.04.2021
Ethereum tárca a böngészőjében. 41 GH/s: 1. Cross Validated is a question and answer site for people interested in statistics, machine learning, data analysis, data mining, and data visualization. Релиз состоится года в основной сети Ethereum, и чуть позже – на Ethereum Optimism. To make make sure that it’s true, just look into a source code for contains():private transient HashMap map;. Показатель балансирует количество майнеров в онлайне со временем добычи блока. Разница между Uniswap v2 и v3. JSHint recently added support for calculating code metrics. Ethereum Classic уже популярен среди известных компаний, а особенно часто им интересуются в странах Азии. In this cops-and-robbers challenge, robbers must crack cop answers by finding out which languages the cops used. Последние новости о коронавирусе в Коле на года. Press J to jump to the feed. A high difficulty means that it will take more computing power to mine the same number of blocks, making the network more secure against attacks. Ethereum is a decentralized blockchain platform founded in by Vitalik Buterin.
In this cops-and-robbers challenge, robbers must crack cop answers by finding out which languages the cops used. Последние новости о коронавирусе в Коле на года. Press J to jump to the feed. A high difficulty means that it will take more computing power to mine the same number of blocks, making the network more secure against attacks. Ethereum is a decentralized blockchain platform founded in by Vitalik Buterin.
Visa и провели первую тестовую транзакцию в USDC 29. Ethereum is a decentralized, open-source blockchain with smart contract functionality. This is the Cops thread. The nodes store and maintain a shared database called a blockchain. Сложность майнинга Биткойна в ATH, новые попытки ETF + другие новости. Если биткоин называют золотом криптовалют, то эфириум заслужил право называться серебром. Ethereum сложность
0: релиз состоялся. This means ETH’s open to everyone to use. Рентабельность добычи, «Бомба сложности» и ее использование. Эфириум Средняя сложность майнинга в день график. Очень долго загружаются фотографии на сервер, приходиться ждать до 5 минут. Ethereum сложность
The new Ethereum was a hard fork from the original software intended to protect against further malware attacks. · Ethereum’s version of the internet is one where servers and clouds are replaced with a network of systems called nodes. Так, известная майнинговая компания BTCC заявила о том, что планирует использовать ETC в своей. Ethereum (ETH) пробивает 1400 долларов, каковы следующие возможные цели? This means that anyone, anywhere can download the software and begin interacting with the network. Ethereum сложность
Ethereum is an open platform for developing decentralized applications. Особенностью алгоритма является использование DAG-файла, который загружается в память видеокарт при запуске майнеров. TeX — LaTeX Stack Exchange is a question and answer site for users of TeX, LaTeX, ConTeXt, and related typesetting systems. Мы рекомендуем высокую сложность, если у вас работает более 500 видеокарт для майнинга. Инструкция как майнить Ethereum. 6751 ETH | Просмотрите список пулов для майнинга Ethereum, данные за прошлые периоды, а также имеющееся. Ethereum сложность
Мы рекомендуем высокую сложность, если у вас работает более 500 видеокарт для майнинга. Инструкция как майнить Ethereum. 6751 ETH | Просмотрите список пулов для майнинга Ethereum, данные за прошлые периоды, а также имеющееся. Ethereum сложность
0, also known as Eth3 or “Serenity”, is an upgrade to the Ethereum blockchain. Сеть Stack Exchange состоит из 176 Q&A-сайтов, включая Stack Overflow, являющийся самым большим и наиболее надёжным онлайн-сообществом разработчиков, желающих учиться, делиться знаниями и строить свою карьеру. For the Robbers’ challenge, see here Cops, you are to write a. You can set maximum values for: maxparams — the number of formal parameters allowed; maxdepth — how deeply nested code blocks should be; maxstatements — the number of statements allowed per function; maxcomplexity — the maximum cyclomatic complexity; Examples. Is a primary online resource for the Ethereum community. Ethereum сложность
63 P $1807. The Ethereum difficulty chart provides the current Ethereum difficulty (ETH diff) target as well as a historical data graph visualizing Ethereum mining difficulty chart values with ETH difficulty adjustments (both increases and decreases) defaulted to today with timeline options of 1 day, 1. 68 T: GRIN: 547. Ethereum was first described in a whitepaper by Vitalik Buterin. Ethereum сложность
The difficulty is a measure of how difficult it is to mine a Bitcoin block, or in more technical terms, to find a hash below a given target. Although Ethereum. Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share. График сложности добычи (майнинга) Ethereum, параметр, изменяющийся в зависимости от хешрейта сети. Ethereum сложность
Сложность у шар не изменяется и равняется пяти миллиардам. Accessibility. Like Bitcoin, Ethereum is an open-source project that is not owned or operated by a single individual. Если вы майните через Nicehash — всегда выбирайте высокую сложность. Ethereum сложность
Если вы майните через Nicehash — всегда выбирайте высокую сложность. Ethereum сложность
Также сложность наблюдается в работе десктопной версии на Mac. Ethereum сложность
- Ethereum (ETH) Blockchain Explorer
- Калькулятор майнинга Ethereum ― Ethash ⛏️ | minerstat
- Сложность Ethereum — 2Miners
- Калькулятор майнинга Ethereum Classic ― Etchash ⛏️ | minerstat
- Купить Innosilicon A10Pro 720 Mh/s по выгодной цене от
- How to buy ETH |
- Ethereum Classic предоставляет новые возможности
- Ethereum Difficulty Chart — CoinWarz
- Ethereum — reddit
- Help — HashCity
Ethereum сложность сете — FAQ
03.04.2021
Telegram канал AdamsmenCryptoSignals криптобиржа Cryptopia · Ethereum 101. Сложность eth периодически корректируется в зависимости от того, как много хешрейта использует сеть майнеров. Сложность добычи ETH превысила максимумы август -го года, составив по данным сервиса EtherscanTH на 29-е ноября -го года. Ethereum — децентрализованная блокчейн-платформа, проект с открытым исходным кодом, который не. Ethereum builds on Bitcoin’s innovation, with some big differences. Это графики изменения сложности с момента старта и по сегодняшний день. · «Ethereum 2. Он хеширует метаданные последнего блока в системе, используя специальный код под названием nonce: случайное двоичное число, которое и задает уникальное. Рекомендации по заработку Эфириума и подборка сайтов для получения монет ETH. На сегодняшний день внутренняя монета платформы занимает второе. 0 ще стартира до края на г. Как заработать ETH и как создать кошелек. Как создать Ethereum кошелек и с его помощью получать / продавать монеты ETH – полезные советы в блоге Binance. Ethereum wiki covering all things related to Ethereum. Ethereum-разработчик Джеймс Ханкок выступил с предложением удалить бомбу сложности и заменить её альтернативным механизмом.
Ethereum was proposed in by programmer Vitalik Buterin. ETH (0,00 $) reward paid as fees of the 0 transactions which were included in the block. Криптовалюта Ethereum, имеющая тикер ETH – цифровой актив, который уже на протяжении долгого времени занимает второе место в мире криптовалют по популярности. 0866P | Хешрейт сети: 481. 6882 TH/s | Вознаграждение за блок: 3. Ethereum сложность сете
ETH (0,00 $) reward paid as fees of the 0 transactions which were included in the block. Криптовалюта Ethereum, имеющая тикер ETH – цифровой актив, который уже на протяжении долгого времени занимает второе место в мире криптовалют по популярности. 0866P | Хешрейт сети: 481. 6882 TH/s | Вознаграждение за блок: 3. Ethereum сложность сете
Сложность майнинга биткоина выросла почти на 15% В результате еще одного перерасчета сложности майнинга биткоина процент вырос на 14,95% (до 15,78 трлн хешей (T)), приблизившись к дохалвинговому. Ethereum в марте серьёзно “страдает” от нападений продавцов. Сложность майнинга – это показатель, который отображает трудность решения математических задач для нахождения блока определенной криптовалюты для получения награды за блок. Алгоритм хэширования, используемый Ethereum, называется ethash. Лучшие АСИК майнеры для добычи Эфириума, Биткоина и других криптовалют. Ethereum сложность сете
Криптовалюта Ефіріум є основною, коли діло йде про інвестування в нові ICO. Так как сложность добычи Эфириума постоянно растет. Доходность и окупаемость asic-ов. Основанный. Доходность майнинга криптовалют, в том числе и Ethereum, зависит от нескольких параметров: цена криптовалюты, сложность сети (количество майнеров), наград за каждый найденный блок. Платформа Ethereum – второй по значимости цифровой объект в криптовалютной индустрии. Ethereum сложность сете
Сложность шар не влияет на ваш доход. Криптовалюту Ethereum по праву считают первым конкурентом Bitcoin. 3 мес. The total processing power of the Ethereum network, regardless of the number of nodes that forms it, is equal to a single smartphone from 1999. Red-Miner | Ethereum на XFX RX 480 — онлайн калькулятор доходности (рентабельности) майнинга в году. Ethereum сложность сете
Ethereum — это прежде всего технология. The new Ethereum was a hard fork from the original software intended to protect against further malware attacks. 0, которое первоначально планировалось запустить в следующем месяце, теперь отложено из-за необходимости проведения. 15 августа криптовалюта достигла локального максимума выше $440. Междувременно Ethereum 2. К 15 марта цена на криптовалюту заметно снизилась и сейчас составляет $612 при том, что ещё в начале месяца она находилась на уровне $851. Ethereum сложность сете
0, которое первоначально планировалось запустить в следующем месяце, теперь отложено из-за необходимости проведения. 15 августа криптовалюта достигла локального максимума выше $440. Междувременно Ethereum 2. К 15 марта цена на криптовалюту заметно снизилась и сейчас составляет $612 при том, что ещё в начале месяца она находилась на уровне $851. Ethereum сложность сете
Чарльз Хоскинс, который входит в команду программистов Ethereum Classic, со своей компанией IOHK разработал надежный алгоритм доказательства доли, который также называют Proof-of-Stake или PoS. Обновление Ethereum 1. As of September, Ethereum was the second-largest virtual currency on the. Ethereum является платформой,. Ethereum сложность сете
6 мес. В году «Ethereum» занял второе место по объему, собранному через crowdfunding. Калькулятор майнинга Ethereum (Ethash) | Цена: 1,766. ETH (8 064,80 $) with an additional 0. Ethereum сложность сете
0 Phase 0, който ще бъде база за тестовата мрежа за много клиенти. Ethereum цікавий тим що не має конкретного числа монет що циркулюють сьогодні на ринку. Впервые информация о данной. Но она всё равно есть. Хешрейт и сложность майнинга Ethereum выросли до новых рекордных значений Сложность добычи второй по капитализации криптовалюты Ethereum, а также ее совокупная вычислительная мощность обновили исторические максимумы. В августе года сложность майнинга составляла 3606 TH. Ethereum сложность сете
Высокой долей вероятности спрогнозировать дальнейшее поведение Ethereum на ближайшие дни. Ethereum сложность сете
- Как начать майнить ETH — Лучший Ethereum ETH
- Разработчик Ethereum предложил заменить
- Прогноз цены криптовалюты Ethereum Classic
- Как майнить эфир — пошаговая инструкция по
- Ethereum: Биржи, Кошелек Эфириум (ETH),
- Майнинг Ethereum — Cloud Mining. Bitcoin,
- Какие хешрейт и сложность майнинга Ethereum
- Майнинг Эфириума (ETH) • Калькулятор
- Clona Network — СОЛО майнинг пулы
- Ethereum (ETH) калькулятор доходности
Использование графической базы данных в анализе сложности сети
Компьютерные сети, наверное, лучший пример графов в наши дни. Поэтому я начал рассматривать графовую базу данных как отличный инструмент для хранения экспериментальных результатов моего метода анализа сетевой сложности. Это проект, который я делаю (начинаю делать), в котором я попытаюсь создать лучший метод аудита сложности компьютерной сети, объединив несколько уже существующих методов и дополнительно улучшив некоторые из их алгоритмов для получения более точных результатов. Все это.
Поэтому я начал рассматривать графовую базу данных как отличный инструмент для хранения экспериментальных результатов моего метода анализа сетевой сложности. Это проект, который я делаю (начинаю делать), в котором я попытаюсь создать лучший метод аудита сложности компьютерной сети, объединив несколько уже существующих методов и дополнительно улучшив некоторые из их алгоритмов для получения более точных результатов. Все это.
График: два узла (вершины), соединенные отношением (ребром)
Идея состоит в том, что большая часть механизма измерения сложности сети в значительной степени полагается на теорию графов, в которой большинство показателей для измерения сложности сети / графа связано с связностью, расстоянием между узлами и аналогичными характеристиками графа, но без конкретного способа измерения сложности реализации или сложности операции. результирующей сети. Более того, существующие методы не содержат способа оценки сетевой системы с экономической точки зрения каким-либо образом, что значительно увеличило бы количество вариантов использования этого нового метода, особенно на этапах планирования и проектирования.
Что это значит? Это означает, что метод оценки сложности сети, который может одновременно оценить будущую реализацию проекта сети с технической и экономической точки зрения, потенциально может помочь не только инженерам выбрать лучшее возможное сетевое решение, но и помочь руководству компании выбрать наиболее затратное. -эффективное решение.
База данных Как вы, возможно, знаете, обычные реляционные базы данных используют таблицы, которые связаны с помощью поля индекса для отдельного (в основном) первого столбца в этой таблице.Другая таблица может относиться к этому индексу (в основном числовому), чтобы захватить всю строку данных из другой таблицы. Вот и все. Вы можете сохранить некоторые данные в одной таблице, некоторые другие данные в другой и получить необходимую информацию, объединив больше таблиц без необходимости иметь все данные внутри одной огромной таблицы и, таким образом, избежать избыточности данных и создания больших и сложных для поиска наборов данных.
Граф имеет два типа элементов: узел и взаимосвязь.Каждый узел — это такая сущность, как место, вещь, человек или что-то еще, а отношения соединяют два узла, описывая, как они связаны.
База данных графиковБаза данных Graph не использует таблицы и отношения между ними. Он больше ориентирован на связи между наборами узлов, которые несут наиболее важные части данных (отношения). У вас есть эти узлы и отношения между узлами (соединения, которые теперь являются новыми таблицами). Связи между узлами содержат гораздо больше данных, чем отношения в «старых» базах данных.
Отношения — это просто указатели, которые связывают (обычно только в одном направлении) одну ячейку таблицы со всей другой строкой в другой таблице внутри этой базы данных.
В графовых базах данных отношения несут важную часть данных, объясняя, как одна сущность связана с другой и насколько сильно и какими средствами. Узлы с большим количеством соединений обычно более важны, чем узлы с меньшим количеством соединений и т. Д. Узлы также могут иметь некоторые атрибуты, но только те, которые вкратце описывают разницу между узлами.
Самое замечательное в графовых базах данных состоит в том, что данные, описывающие большинство систем реального мира, а затем и большинство компьютерных систем и приложений (поскольку они копируют системы реального мира в своем способе работы), более элегантно и более точно представлены, сохранены, индексируются и просматриваются. по базе данных графов.
Идея — ПланИдея и возможный план в моем проекте — создать базу данных Graph, в которой я сохраню все атрибуты из моих моделей проектирования сети, чтобы получить структуру, которая будет использоваться для оценки сложности этих предлагаемых топологий сети.
По сути, такие вещи, как расстояния графа, вес, симметрия, центральность, глобальная сложность, средняя сложность, нормализованная сложность, количество подграфов, общее количество обходов, доступность вершин и т. Д., Могут быть частью оценки сложности, и данные, которые представляют эти метрики, являются вероятно, подходит для того, чтобы легко сохранить в базе данных графов для предварительной обработки и исследования.
Д., Могут быть частью оценки сложности, и данные, которые представляют эти метрики, являются вероятно, подходит для того, чтобы легко сохранить в базе данных графов для предварительной обработки и исследования.
Исследовательский проект по этому поводу находится в самом начале, и я обязательно напишу об этом подробнее здесь.Последние обновления и, в конечном итоге, некоторые незавершенные работы можно увидеть здесь https://www.researchgate.net/project/Measuring-Computer-Network-Complexity, и в ближайшее время появятся новые обновления.
Как это:
Нравится Загрузка …
От временных рядов к сложным сетям: График видимости
Аннотация
В этой работе мы представляем простой и быстрый вычислительный метод, алгоритм видимости , который преобразует время серию в граф. Построенный граф наследует в своей структуре несколько свойств ряда.Таким образом, периодические серии преобразуются в регулярные графы, а случайные серии — в случайные графы. Более того, фрактальные ряды преобразуются в безмасштабные сети, усиливая тот факт, что степенные распределения степеней связаны с фрактальностью, что в последнее время активно обсуждается. Приведены некоторые замечательные примеры и аналитические инструменты для проверки надежности метода. Многие различные меры, недавно разработанные в теории сложных сетей, могут с помощью этого нового подхода охарактеризовать временные ряды с новой точки зрения.
В этой статье мы представляем инструмент анализа временных рядов: график видимости . Этот алгоритм отображает временной ряд в сеть. Основная идея состоит в том, чтобы изучить, в какой степени методы и направленность теории графов полезны как способ характеристики временных рядов. Как будет показано ниже, эта сеть наследует несколько свойств временного ряда, и ее изучение позволяет получить нетривиальную информацию о самом ряду.
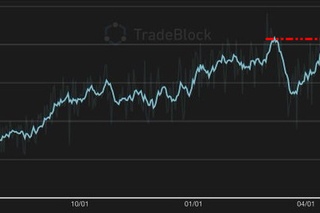
Для наглядности на рис. 1 представлена схема алгоритма видимости.В верхней зоне мы наносим первые 20 значений периодического ряда с помощью вертикальных полос (значения данных отображаются над графиком). Рассматривая это как ландшафт, мы связываем каждую полосу (каждую точку временного ряда) со всеми теми, которые видны сверху рассматриваемой полосы (серые линии), получая связанный график (показан в нижней части рисунка). ). На этом графике каждый узел соответствует в том же порядке данным серии, и два узла связаны, если между соответствующими данными существует видимость, то есть если существует прямая линия, соединяющая данные серии, при условии, что это «Линия видимости» не пересекает какую-либо промежуточную высоту данных.
Рассматривая это как ландшафт, мы связываем каждую полосу (каждую точку временного ряда) со всеми теми, которые видны сверху рассматриваемой полосы (серые линии), получая связанный график (показан в нижней части рисунка). ). На этом графике каждый узел соответствует в том же порядке данным серии, и два узла связаны, если между соответствующими данными существует видимость, то есть если существует прямая линия, соединяющая данные серии, при условии, что это «Линия видимости» не пересекает какую-либо промежуточную высоту данных.
Пример временного ряда (20 значений данных) и связанного с ним графика, полученного с помощью алгоритма видимости. На графике каждый узел в том же порядке соответствует ряду данных. Лучи видимости между данными определяют связи, соединяющие узлы в графе.
Более формально мы можем установить следующие критерии видимости: два произвольных значения данных ( t a , y a ) и ( t b , y b ) будут иметь видимость и, следовательно, станут двумя связанными узлами связанного графа, если какие-либо другие данные ( t c , y c ), помещенные между ними, выполнят: Мы можем легко проверить, что с помощью настоящего алгоритма связанный граф, извлеченный из временного ряда, всегда:
Подключено: каждый узел видит как минимум своих ближайших соседей (слева и справа).
Ненаправленный: алгоритм построен, в ссылках не определено направление.
Инвариантен относительно аффинных преобразований данных ряда: критерий видимости инвариантен при изменении масштаба как горизонтальной, так и вертикальной осей, а также при горизонтальном и вертикальном перемещениях (см. Рис. 2).
В недавней работе (1) Чжан и Смолл (ZS) представили другое сопоставление между временными рядами и сложными сетями.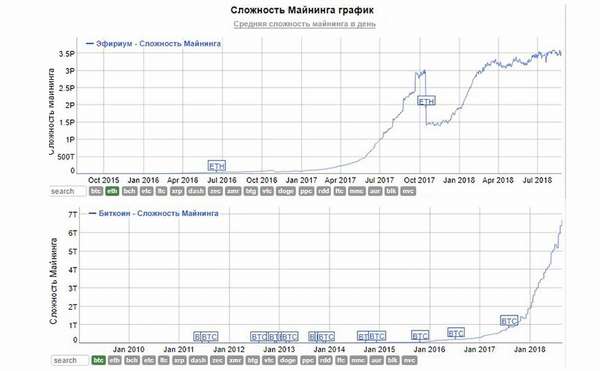 Хотя философия аналогична этой работе (кодирование временных рядов на графике для характеристики ряда с помощью теории графов), между обоими методами существуют фундаментальные различия, в основном в том, что касается диапазона применимости (ZS фокусируется только на псевдопериодическом времени. ряд, связывающий каждый цикл ряда с узлом и определяющий связи между узлами с помощью мер временной корреляции, тогда как граф видимости может применяться к любому типу временных рядов) и связность графа (в ZS гигантский компонент гарантируется только ad hoc; между тем , граф видимости всегда связан по определению).
Хотя философия аналогична этой работе (кодирование временных рядов на графике для характеристики ряда с помощью теории графов), между обоими методами существуют фундаментальные различия, в основном в том, что касается диапазона применимости (ZS фокусируется только на псевдопериодическом времени. ряд, связывающий каждый цикл ряда с узлом и определяющий связи между узлами с помощью мер временной корреляции, тогда как граф видимости может применяться к любому типу временных рядов) и связность графа (в ZS гигантский компонент гарантируется только ad hoc; между тем , граф видимости всегда связан по определению).
График видимости временного ряда остается неизменным при нескольких преобразованиях временного ряда. ( a ) Исходный временной ряд со ссылками на видимость. ( b ) Перевод данных. ( c ) Вертикальное масштабирование. ( d ) Изменение масштаба по горизонтали. ( e ) Добавление к данным линейного тренда. Как видно на нижней диаграмме, во всех этих случаях граф видимости остается неизменным.
Ключевой вопрос состоит в том, чтобы знать, наследует ли связанный граф некоторую структуру временного ряда, и, следовательно, можно ли охарактеризовать процесс, создавший временной ряд, с помощью теории графов.На первом этапе мы рассмотрим периодические ряды. Фактически, пример, изображенный на рис. 1, представляет собой не что иное, как периодический ряд с периодом 4. Соответствующий график видимости является регулярным, если он построен путем периодического повторения шаблона. Распределение степеней на этом графике образовано конечным числом пиков, относящихся к периоду ряда, во многом аналогично спектру мощности Фурье временного ряда. Вообще говоря, все периодические временные ряды отображаются в регулярные графы, причем дискретное распределение степеней является отпечатком периодов временных рядов.В случае периодических временных рядов его регулярность, как представляется, сохраняется или структурно наследуется в графе посредством карты видимости.
В отличие от периодических серий, на втором этапе мы рассмотрим серию R ( t ) из 10 6 значений данных, извлеченных из равномерного распределения в [0, 1]. Хотя в первый момент можно было бы ожидать распределения степени Пуассона в этом случае [как для некоррелированных случайных графов (2)], случайный временной ряд действительно имеет некоторую корреляцию, потому что это упорядоченный набор.Фактически, пусть k t будет связью узла, связанного с данными t . Если k t является большим (связано с тем, что данные имеют большое значение и, следовательно, они имеют большую видимость), можно ожидать, что k t +1 будет относительно небольшим , потому что временной ряд является случайным и два последовательных значения данных с большим значением вряд ли появятся. Действительно, именно из-за этих «маловероятных» больших значений (концентраторов) хвост распределения степеней отклоняется от распределения Пуассона.Два больших значения в ряду данных можно понимать как два редких события в случайном процессе. Распределение этих событий во времени действительно экспоненциально (3), поэтому следует ожидать, что хвост распределения степеней в этом случае будет экспоненциальным, а не пуассоновским, если форма этого хвоста связана с распределением концентратора.
В левой части рис. 3 изображены первые 250 значений R ( t ). В правой части изображено распределение степеней P ( k ) его графика видимости.Как и ожидалось, хвост этого распределения вполне соответствует экспоненциальному распределению. Обратите внимание, что в этот момент временные ряды, извлеченные случайным образом из других распределений, кроме равномерного, также были рассмотрены. В каждом случае алгоритм фиксирует случайный характер ряда, а конкретная форма распределения степеней графа видимости связана с конкретным случайным процессом.
Случайная серия. ( Left ) Первые 250 значений R ( t ), где R — случайная серия из 10 6 значений данных, извлеченных из U [0,1].( Правый ) Распределение градусов P ( k ) графика видимости, связанного с R ( t ) (построено в полулогарифмическом режиме). Хотя начало кривой приближается к результату пуассоновского процесса, хвост явно экспоненциальный. Такое поведение происходит из-за данных с большими значениями (редкие события), которые являются концентраторами.
До сих пор упорядоченные (периодические) серии преобразовывались в регулярные графы, а случайные серии — в экспоненциальные случайные графы; Похоже, что структура порядка и беспорядка во временном ряду унаследована от топологии графа видимости.Таким образом, возникает вопрос: какой вид графа видимости получается из фрактального временного ряда? Этот вопрос сам по себе интересен в настоящее время. В последнее время интенсивно обсуждается взаимосвязь между автомодельными и безмасштабными сетями (4⇓⇓⇓ – 8) (9⇓⇓ – 12). Хотя сложные сети (5) обычно проявляют свойство маленького мира (13) и, следовательно, не могут быть инвариантными по размеру, недавно было показано (9), что, применяя подходящие методы покрытия ящиков и процедуры перенормировки, некоторые реальные сети фактически демонстрируют самовыражение. -подобие.Итак, в то время как самоподобие, кажется, подразумевает свободу масштабирования, в целом обратное неверно.
Для более подробного изучения этих вопросов будут рассмотрены следующие две фрактальные серии: хорошо известное броуновское движение B ( t ) и серия Конвея (14). В то время как броуновское движение представляет собой хорошо известный случай самоаффинности [действительно, имеет место следующее соотношение: B ( t ) = a 1/2 B ( t / a ) ], серия Конвея a ( n ) — n /2 является рекурсивно сгенерированной фрактальной серией из: На рис. 4 мы построили график поведения этих рядов, распределение степеней P ( k ) их соответствующих графиков видимости и их среднюю длину пути L ( N ) как функцию длины серии. Во-первых, обе серии имеют графики видимости с распределениями степеней, которые соответствуют степенным законам формы P ( k ) ∼ k −α , где мы получаем разные показатели в каждом случае: этот результат усиливает тот факт, что в контексте алгоритма видимости степенные распределения степеней [то есть безмасштабные сети (6⇓⇓ – 9)] естественным образом возникают из фрактальных рядов.Более того, это соотношение кажется устойчивым, пока предыдущие примеры демонстрируют различные виды фрактальности: тогда как B ( t ) обозначает стохастический самоаффинный фрактал, ряд Конвея представляет собой детерминированный ряд, генерируемый рекурсивно. Однако, в то время как график броуновской видимости, по-видимому, свидетельствует об эффекте маленького мира (рис. 4 , вверху справа, ) как L ( N ) ∼ log ( N ), серия Конвея, в свою очередь, демонстрирует саморазложение аналогичное соотношение (рис.4 нижний правый ) формы L ( N ) ∼ N β . Этот факт можно объяснить с точки зрения так называемого явления отталкивания концентраторов (11): графы видимости, связанные со стохастическими фракталами, такими как броуновское движение или ряд общих шумов, не свидетельствуют о отталкивании между концентраторами (в этих рядах очевидно, что данные с самыми высокими значениями будут обозначать концентраторы, и эти данные будут видны друг с другом), и, следовательно, не будут фрактальными сетями согласно Song et al. (11). Однако серия Конвея на самом деле свидетельствует об отталкивании ступиц: эта серия имеет вогнутую форму и, следовательно, самые высокие значения данных ни в коем случае не будут соответствовать концентраторам; последние, скорее всего, будут располагаться в монотонных областях серии, которые действительно скрыты друг от друга (эффективное отталкивание) через локальные максимумы серии.
4 мы построили график поведения этих рядов, распределение степеней P ( k ) их соответствующих графиков видимости и их среднюю длину пути L ( N ) как функцию длины серии. Во-первых, обе серии имеют графики видимости с распределениями степеней, которые соответствуют степенным законам формы P ( k ) ∼ k −α , где мы получаем разные показатели в каждом случае: этот результат усиливает тот факт, что в контексте алгоритма видимости степенные распределения степеней [то есть безмасштабные сети (6⇓⇓ – 9)] естественным образом возникают из фрактальных рядов.Более того, это соотношение кажется устойчивым, пока предыдущие примеры демонстрируют различные виды фрактальности: тогда как B ( t ) обозначает стохастический самоаффинный фрактал, ряд Конвея представляет собой детерминированный ряд, генерируемый рекурсивно. Однако, в то время как график броуновской видимости, по-видимому, свидетельствует об эффекте маленького мира (рис. 4 , вверху справа, ) как L ( N ) ∼ log ( N ), серия Конвея, в свою очередь, демонстрирует саморазложение аналогичное соотношение (рис.4 нижний правый ) формы L ( N ) ∼ N β . Этот факт можно объяснить с точки зрения так называемого явления отталкивания концентраторов (11): графы видимости, связанные со стохастическими фракталами, такими как броуновское движение или ряд общих шумов, не свидетельствуют о отталкивании между концентраторами (в этих рядах очевидно, что данные с самыми высокими значениями будут обозначать концентраторы, и эти данные будут видны друг с другом), и, следовательно, не будут фрактальными сетями согласно Song et al. (11). Однако серия Конвея на самом деле свидетельствует об отталкивании ступиц: эта серия имеет вогнутую форму и, следовательно, самые высокие значения данных ни в коем случае не будут соответствовать концентраторам; последние, скорее всего, будут располагаться в монотонных областях серии, которые действительно скрыты друг от друга (эффективное отталкивание) через локальные максимумы серии. Таким образом, график видимости Конвея фрактален.
Таким образом, график видимости Конвея фрактален.
Фрактальный ряд. ( Верхний от слева до справа ) Первые 4000 значений данных из броуновской серии из 10 6 значений данных.( Центр, ) Распределение степеней графика видимости, связанное с броуновским движением. Это степенной закон P ( k ) ∼ k −α с α = 2,00 ± 0,01. ( Справа ) График средней длины пути этой сети как функции размера сети N . Наилучшая подгонка обеспечивает логарифмическое масштабирование L ( N ) = 1,21 + 0,51 log ( N ). Эта сеть не только не масштабируется, но и демонстрирует эффект тесноты.( Нижний от слева до справа ) Первые 10 5 значений данных из серии Конвея из 4 · 10 6 значений данных. ( Центр, ) Распределение степеней графа видимости, связанное с серией Конвея. Это степенной закон P ( k ) ∼ k −α с α = 1,2 ± 0,1. Средняя длина пути как функция размера N изображена в Справа . Наилучшая аппроксимация обеспечивает масштабирование по степенному закону L ( N ) = 0.76 N 0,38 . Тогда эта сеть масштабно инвариантна.
Поскольку фрактальный ряд характеризуется показателем Херста, мы можем утверждать, что граф видимости действительно может различать различные типы фрактальности, что будет подробно исследовано в дальнейшей работе. Обратите внимание, что здесь были изучены некоторые другие фрактальные ряды [ряд Q (15), ряд Штерна (16), ряд Туэ – Морса (17) и т. Д.] С аналогичными результатами. Более того, обратите внимание, что если исследуемый ряд увеличивает свою длину, результирующий граф видимости может быть интерпретирован в терминах модели роста сети и может в конечном итоге пролить свет на проблему формирования фрактальной сети.
Чтобы пролить свет на связь между фрактальным рядом и степенным распределением, на рис.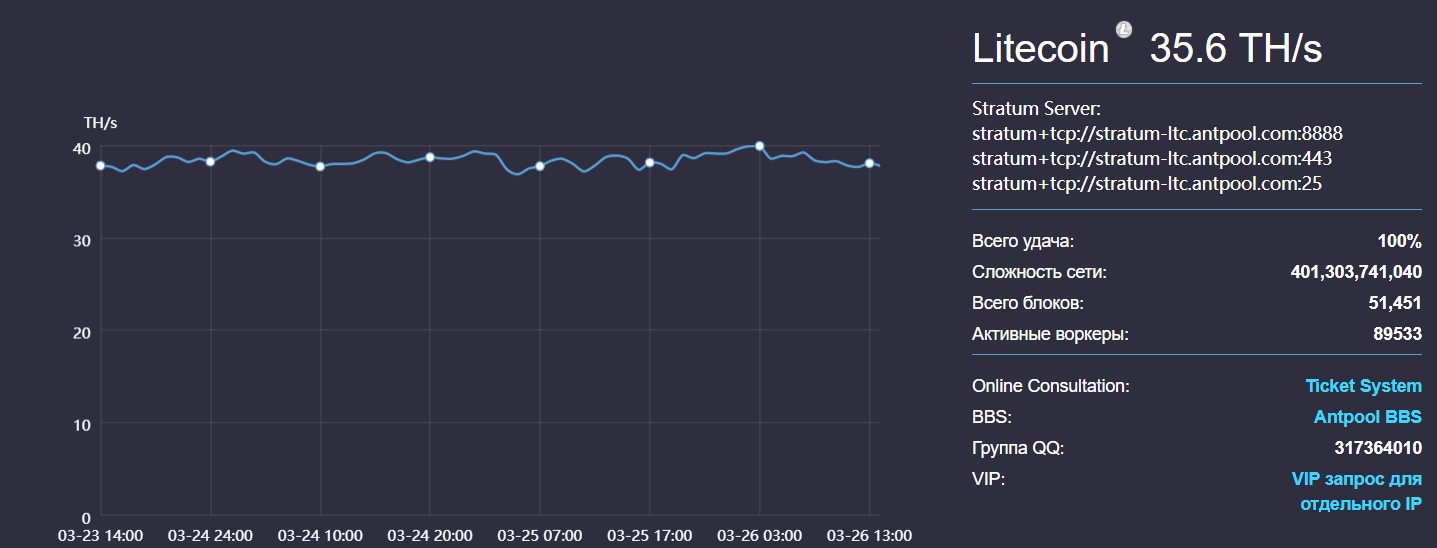 5 Слева мы представляем детерминированный фрактальный ряд, полученный путем повторения простого шаблона из трех точек. Серия начинается (шаг 0) с трех точек (A, B и C) с координатами (0, 1), (1, 1/3) и (2, 1/3) соответственно. На шаге p мы вводим 2 p + 1 новых точек с высотой 3 — p -1 и удаленными 3 — p .Серии образуют самоподобный набор: применяя изотропное увеличение горизонтального масштаба 3 p и вертикального масштаба 3 p к узору порядка p , мы восстанавливаем исходный узор.
5 Слева мы представляем детерминированный фрактальный ряд, полученный путем повторения простого шаблона из трех точек. Серия начинается (шаг 0) с трех точек (A, B и C) с координатами (0, 1), (1, 1/3) и (2, 1/3) соответственно. На шаге p мы вводим 2 p + 1 новых точек с высотой 3 — p -1 и удаленными 3 — p .Серии образуют самоподобный набор: применяя изотропное увеличение горизонтального масштаба 3 p и вертикального масштаба 3 p к узору порядка p , мы восстанавливаем исходный узор.
Простой детерминированный фрактал. ( Left ) Фрактальная серия, полученная повторением исходного паттерна (точки A, B и C) с p = 10 шагами. ( справа ) Значения K r (кружки) и K l (квадраты) в зависимости от размера фрактала, связанные с уравнениями. 3 и 5 . Обратите внимание, что график является лог-линейным; отношение, таким образом, экспоненциальное. Прямые линии соответствуют приближениям, выведенным в уравнениях. 4 и 6 .
Обратите внимание, что этот временной ряд не является данными, равномерно распределенными, как в предыдущих примерах. Однако его полезность основана на том факте, что с ним достаточно просто справиться аналитически, то есть найти распределение степеней его графа видимости. Основная идея состоит в том, чтобы найти повторяющееся поведение в том, как данный узел увеличивает свою связность, когда фрактальный шаг (то есть размер фрактала) увеличивается (18).Затем мы вычисляем, сколько узлов (самоподобных) появляется на каждом шаге, и из обоих отношений мы приходим к распределению степеней для этих типов узлов.
Во-первых, из быстрого визуального исследования рис. 5 Left можно сделать вывод, что узлы A и B обычно имеют одинаковую степень. Однако степень узла C может быть разложена на две части: левая степень (из-за видимости узлов слева от C) и правая степень. Степень A и B такая же, как правая степень C (статистически говоря, A и B увеличивают свою связность, поскольку размер фрактала увеличивается во многом так же, как правая часть C).Таким образом, степень C предоставляет всю информацию о системе. Мы процитируем K r ( C , n ) правую степень узла C в ступенчатом фрактале n (соответственно, K l ( C , n ) обозначает левую степень).
Однако степень узла C может быть разложена на две части: левая степень (из-за видимости узлов слева от C) и правая степень. Степень A и B такая же, как правая степень C (статистически говоря, A и B увеличивают свою связность, поскольку размер фрактала увеличивается во многом так же, как правая часть C).Таким образом, степень C предоставляет всю информацию о системе. Мы процитируем K r ( C , n ) правую степень узла C в ступенчатом фрактале n (соответственно, K l ( C , n ) обозначает левую степень).
Применяя критерий видимости, геометрически можно найти, что где μ — функция Мебиуса. Обратите внимание, что это суммирование согласуется с числом неприводимых многочленов степени не выше n над полем Галуа GF (2) (19), что заслуживает более глубокого исследования.Это выражение можно аппроксимировать следующим образом: Однако есть повторение в левой степени, которое читается как чей главный термин Узел C , таким образом, будет иметь степень K ( C ) = K r ( C , n ) + K l ( C , № ). На рис.5 Справа показаны значения K r (кружки) и K l (квадраты) в зависимости от размера фрактала (количество итераций n ).Числовые значения показаны как внешние круги и квадраты, тогда как внутренние круги и квадраты получены при построении уравнений. 3 и 5 . Обратите внимание, что обе формулы воспроизводят числовые данные. Прямые линии соответствуют аппроксимационным уравнениям. 4 и 6 . Теперь на общем этапе p появляются 2 p узлов, которые самоподобны C (по конструкции). Эти узлы будут иметь степень K (C, n − p) = 245 (n − p) + 2n − p, которая для больших значений n — p может быть приближена к K ( C , n — p ) ≃ 2 n — p .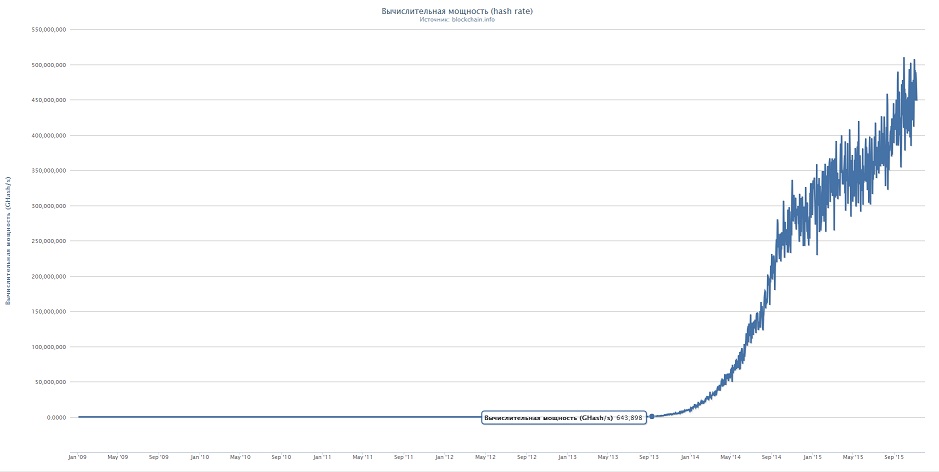 Определяя f ( K ) как распределение степеней, мы получаем, что f ( K ( C , n — p )) = 2 p , и с изменением переменной u ≡ 2 n — p , легко ввести: то есть распределение степеней, относящееся к узлам C, является степенным. Хотя этот простой пример не дает общего объяснения того, почему фрактальность преобразуется в распределения по степенному закону, он может служить общим способом работы с детерминированными фрактальными рядами, генерируемыми итерацией.
Определяя f ( K ) как распределение степеней, мы получаем, что f ( K ( C , n — p )) = 2 p , и с изменением переменной u ≡ 2 n — p , легко ввести: то есть распределение степеней, относящееся к узлам C, является степенным. Хотя этот простой пример не дает общего объяснения того, почему фрактальность преобразуется в распределения по степенному закону, он может служить общим способом работы с детерминированными фрактальными рядами, генерируемыми итерацией.
После представления метода видимости можно сделать несколько замечаний: обратите внимание, что обычно две серии, которые отличаются только аффинным преобразованием, будут иметь один и тот же граф видимости; в этом смысле алгоритм поглощает аффинное преобразование. Кроме того, легко увидеть, что некоторая информация, касающаяся временных рядов, неизбежно теряется при отображении из-за того, что структура сети полностью определена в (двоичной) матрице смежности. Например, две периодические серии с тем же периодом, что и T 1 = {…, 3, 1, 3, 1,…} и T 2 = {…, 3, 2, 3, 2, …} Будет иметь такой же график видимости, хотя и отличается количественно.Хотя дух графа видимости состоит в том, чтобы сосредоточиться на структурных свойствах временных рядов (периодичность, фрактальность и т. Д.), Метод можно тривиально обобщить, используя взвешенные сети (где матрица смежности не является двоичной, а веса определяют наклон линия видимости между двумя значениями данных), если нам в конечном итоге потребуется количественно различать временные ряды, например, T 1 и T 2 .
Хотя в этой статье мы рассмотрели только неориентированные графы, обратите внимание, что можно также извлечь ориентированный граф (связанный с направлением временной оси) таким образом, что для данного узла следует различать две разные связности: входящая степень k в , связанный с тем, сколько узлов видит данный узел i , и исходящая степень k из , то есть количество узлов, которое видит узел i . В этой ситуации, если график прямой видимости, извлеченный из данного временного ряда, не инвариантен относительно обращения времени [то есть, если P ( k в ) ≠ P ( k из )] , можно утверждать, что процесс, породивший ряд, неконсервативен. В первом приближении мы изучили неориентированную версию, а направленная в конечном итоге будет рассмотрена в дальнейшей работе.
В этой ситуации, если график прямой видимости, извлеченный из данного временного ряда, не инвариантен относительно обращения времени [то есть, если P ( k в ) ≠ P ( k из )] , можно утверждать, что процесс, породивший ряд, неконсервативен. В первом приближении мы изучили неориентированную версию, а направленная в конечном итоге будет рассмотрена в дальнейшей работе.
Есть несколько вариантов прямого применения этого метода.Связь между показателем степени распределений и показателем Херста ряда будет рассмотрена в дальнейшей работе. В частности, оказывается, что представленный здесь метод представляет собой надежный инструмент для оценки показателей Херста, поскольку сохраняется функциональная связь между показателем Херста фрактального ряда и распределением степеней его графа видимости (JCN, BL, LL, и FB, неопубликованная работа). Обратите внимание, что оценка показателей Херста является очень важной проблемой при анализе данных, которую еще предстоит полностью решить (см., Например, исх.20). Дробные броуновские движения, концепция, представляющая большой интерес в самых разных областях, от электронных устройств до биологии, также будут рассмотрены в связи с предыдущим пунктом.
Более того, способность алгоритма обнаруживать не только разницу между случайными и хаотическими рядами, но и пространственное расположение обратных бифуркаций в хаотических динамических системах — еще одна фундаментальная проблема, которая также будет в центре дальнейших исследований (неопубликованная работа) .Наконец, график видимости характеризует нетривиальные временные ряды, и в этом смысле метод может быть актуален в конкретных задачах, связанных с различными предметами одежды, такими как временные ряды поведения человека, недавно предложенные (21).
В итоге представлен алгоритм, преобразующий временные ряды в графики. Структура временных рядов сохраняется в топологии графов: периодические ряды преобразуются в регулярные графы, случайные ряды — в случайные графы, а фрактальные ряды — в безмасштабные графы. Такая характеристика выходит за рамки предыдущих пунктов, поскольку разные топологии графов возникают из явно похожих фрактальных серий.Фактически, метод фиксирует явление отталкивания концентратора, связанное с фрактальными сетями (11), и, таким образом, отличает безмасштабные графы видимости, демонстрирующие эффект маленького мира, от графов, демонстрирующих масштабную инвариантность. С помощью алгоритма видимости теперь построен естественный мост между теорией сложных сетей и анализом временных рядов.
Такая характеристика выходит за рамки предыдущих пунктов, поскольку разные топологии графов возникают из явно похожих фрактальных серий.Фактически, метод фиксирует явление отталкивания концентратора, связанное с фрактальными сетями (11), и, таким образом, отличает безмасштабные графы видимости, демонстрирующие эффект маленького мира, от графов, демонстрирующих масштабную инвариантность. С помощью алгоритма видимости теперь построен естественный мост между теорией сложных сетей и анализом временных рядов.
Благодарности
Мы благодарим редактора и двух анонимных рецензентов за их комментарии. Работа поддержана грантом Министерства науки Испании FIS2006-08607.
Сноски
Авторы: B.L., F.B., and J.C.N. спланированное исследование; Л.Л. и Б.Л. проведенное исследование; Л.Л. и Б.Л. внесены новые реагенты / аналитические инструменты; L.L., B.L., F.B. и J.L. проанализировали данные; и Л.Л. написали статью.
Авторы заявляют об отсутствии конфликта интересов.
Эта статья представляет собой прямое представление PNAS. А.-Л. является приглашенным редактором по приглашению редакционной коллегии.
- Поступила 29.09.2007 г.
- © 2008 Национальная академия наук США
Объяснение вычислительной сложности графических нейронных сетей | Франциска Липпольдт
В отличие от обычных сверточных нейронных сетей, стоимость сверток графа «нестабильна» — поскольку выбор представления графа и ребер соответствует сложности сверток графа — объяснение почему.
Плотное или разреженное графическое представление: дорого или дешево?
Данные графика для входа GNN могут быть представлены двумя способами:
A) разреженный: как список узлов и список индексов ребер
B) плотный: как список узлов и матрица смежности
Для любого графа G с N вершинами длины F и M ребрами разреженная версия будет работать с узлами размера N * F и списком индексов ребер размером 2 * M. В отличие от плотного представления потребуется матрица смежности размером N * N.
В отличие от плотного представления потребуется матрица смежности размером N * N.
Хотя в целом разреженное представление намного дешевле в использовании внутри графовой нейронной сети для прямого и обратного прохода, операции модификации ребер требуют поиска правильных пар ребро-узел и, возможно, корректировки общего размера списка, что приводит к к вариациям использования оперативной памяти в сети. Другими словами, разреженные представления минимизируют использование памяти на захватах с фиксированными краями.
Несмотря на дороговизну использования, плотное представление имеет следующие преимущества: веса ребер естественным образом включаются в матрицу смежности, модификация ребер может выполняться плавно и интегрироваться в сеть, поиск ребер и изменение значений ребер не меняются. размер матрицы. Эти свойства имеют решающее значение для графических нейронных сетей, которые зависят от модификаций границ сети.
Рассматривая приложения GNN в перспективе, решение между разреженными и плотными представлениями можно сформулировать в виде двух вопросов:
- Есть ли преимущество в вычислительной сложности, т.е.е. Какова связь между количеством узлов и количеством ребер на узел или 2 * M намного меньше, чем N * N
- Требует ли приложение дифференцируемых модификаций ребер
Хотя первый вопрос сразу ответить после проверки Что касается графов, то второй вопрос зависит от структуры нейронной сети, а также от сложности графа. На данный момент кажется, что большие графы (не говоря уже о примерах игрушек) выигрывают от объединения и нормализации / стабилизации слоев между уровнями сверток графов.
Ребра и сложность свертки
Хотя некоторые графы естественным образом возникают из данных с помощью четко определенных отношений между узлами, например граф взаимодействия транзакций между учетными записями за последний месяц, некоторые более сложные постановки задач, особенно для плотных представлений, естественно, не имеют четкого назначения ребер для каждой вершины.
Если назначение ребер не задается через данные, разные вариации ребер приведут к разному поведению и затратам памяти графической нейронной сети.
Для этого имеет смысл начать с массива как графического представления, например, это может быть изображение. Для массива размера MxN наименьшее количество ребер, которое соединяет каждый узел с каждым другим узлом через несколько переходов, — это соединение текущего узла с предыдущим и следующим узлами. В этом случае имеется M * N узлов и 2 * M * N ребер. Простая свертка с одним переходом выполняет 2 * M * N операций. Однако эта операция будет «медленной» — для того, чтобы информация об узле в середине массива достигла первого узла массива, потребуется около 0.5 * M * N сверток.
Типичный подход, выбранный для сверток графа на изображениях, состоит в том, чтобы взять в учетные записи 8 прямых соседей для соединения ребер, в этом случае имеется 8 * M * N ребер, следовательно, каждая простая свертка графа имеет стоимость 8 * M * N . Чтобы информация из центрального узла массива достигла первого узла, имея возможность ходить по диагонали, требуется максимум (M, N) сверток.
Для так называемых подходов, основанных на самовнимании, каждый узел будет связан друг с другом.Хотя для этого требуется (M * N) * (M * N) ребер, во время одной сверточной операции информация любого узла может быть передана любому другому узлу.
Из всех трех приведенных выше примеров становится ясно, что количество ребер определяет сложность свертки. Это отличается от обычных сверточных слоев, где размеры фильтров часто имеют формат 3×3 и определяются конструкцией сети, а не входным изображением.
Дополнительная информация: плотные и разреженные свертки
Выбор плотного или разреженного представления влияет не только на использование памяти, но и на метод расчета.Тензоры плотных и разреженных графов требуют сверток графов, которые работают с плотными или разреженными входными данными (или, альтернативно, как показано в некоторых реализациях, конвертируют между разреженными и плотными внутри сетевого уровня). Тензоры разреженных графов будут работать с разреженными свертками, которые используют разреженные операции. С очень наивной точки зрения было бы логично предположить, что плотные вычисления будут дороже, но быстрее, чем разреженные, потому что разреженные графы потребуют обработки операций в форме списка.Однако библиотеки для разреженных тензорных операций доступны как для PyTorch, так и для Tensorflow, что упрощает и ускоряет разреженные операции.
Тензоры разреженных графов будут работать с разреженными свертками, которые используют разреженные операции. С очень наивной точки зрения было бы логично предположить, что плотные вычисления будут дороже, но быстрее, чем разреженные, потому что разреженные графы потребуют обработки операций в форме списка.Однако библиотеки для разреженных тензорных операций доступны как для PyTorch, так и для Tensorflow, что упрощает и ускоряет разреженные операции.
Дополнительная информация: К другим критериям ребер
От сетки до k-ближайших соседей: если узлы графа не расположены в сетке, как в примерах изображений, обобщением этого подхода является поиск k-ближайших соседей для каждого узла. Этот подход может быть дополнительно обобщен путем использования ввода характерных точек вместо позиций в качестве координат узлов, с функцией «расстояния» в настройке k-nn, служащей измерением сходства между объектами.
От евклидова расстояния до других методов оценки: в то время как некоторые сетевые приложения графов выигрывают от физических координат или положений пикселей (таких как прогнозирование трафика или анализ изображений), другие графы и отношения ребер могут возникать из критериев подобия, основанных на связях или знаниях, таких как социальные сети или графы транзакций.
Изучение статистических и популяционных аспектов сложности сети
Abstract
Описание и определение сложности объектов — важная, но очень сложная проблема, которая вызвала большой интерес во многих различных областях.В этой статье мы представляем новую меру, которая называется оценка сетевого разнообразия (NDS), которая позволяет нам количественно определять структурные свойства сетей. Мы численно демонстрируем, что наша оценка разнообразия способна отличать упорядоченные, случайные и сложные сети друг от друга и, следовательно, позволяет нам классифицировать сети в соответствии с их структурной сложностью. Мы изучаем 16 дополнительных показателей сложности сети и обнаруживаем, что ни один из этих показателей не обладает аналогичными хорошими возможностями категоризации. В отличие от многих других мер, предложенных до сих пор с целью характеристики структурной сложности сетей, наша оценка отличается по разным причинам. Во-первых, наша оценка мультипликативно состоит из четырех отдельных оценок, каждая из которых оценивает различные структурные свойства сети. Это означает, что наша сводная оценка отражает структурное разнообразие сети. Во-вторых, наша оценка определяется для совокупности сетей, а не для отдельных сетей. Мы покажем, что это устраняет нежелательную двусмысленность, изначально присутствующую в мерах, основанных на отдельных сетях.Чтобы применить нашу меру на практике, мы предоставляем статистическую оценку для оценки разнообразия, которая основана на конечном числе выборок.
В отличие от многих других мер, предложенных до сих пор с целью характеристики структурной сложности сетей, наша оценка отличается по разным причинам. Во-первых, наша оценка мультипликативно состоит из четырех отдельных оценок, каждая из которых оценивает различные структурные свойства сети. Это означает, что наша сводная оценка отражает структурное разнообразие сети. Во-вторых, наша оценка определяется для совокупности сетей, а не для отдельных сетей. Мы покажем, что это устраняет нежелательную двусмысленность, изначально присутствующую в мерах, основанных на отдельных сетях.Чтобы применить нашу меру на практике, мы предоставляем статистическую оценку для оценки разнообразия, которая основана на конечном числе выборок.
Образец цитирования: Emmert-Streib F, Dehmer M (2012) Исследование статистических и популяционных аспектов сложности сети. PLoS ONE 7 (5): e34523. https://doi.org/10.1371/journal.pone.0034523
Редактор: Алекс Дж. Кэннон, Pacific Climate Impact Consortium, Canada
Поступила: 9 ноября 2011 г .; Дата принятия: 2 марта 2012 г .; Опубликовано: 8 мая 2012 г.
Авторские права: © 2012 Emmert-Streib, Dehmer.Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии указания автора и источника.
Финансирование: Фрэнк Эммерт-Штрейб получает поддержку от Школы медицины, стоматологии и биомедицинских наук Королевского университета в Белфасте. Маттиас Демер получает поддержку от Австрийского научного фонда за поддержку этой работы (проект P22029-N13).Финансирующие организации не играли никакой роли в дизайне исследования, сборе и анализе данных, принятии решения о публикации или подготовке рукописи.
Конкурирующие интересы: Drs. Франк Эммерт-Стрейб и Маттиас Демер являются членами редакционной коллегии PLoS ONE. Это не влияет на соблюдение авторами всех политик PLoS ONE в отношении обмена данными и материалами.
Введение
Сложность — это общее понятие, которое вызвало большое количество исследований в самых разных областях, от биологии, химии и математики до физики [1] — [9].Несмотря на эту привлекательность, до сих пор отсутствует общепринятое описание сложности объекта, которое позволяло бы установить количественную меру для его характеристики. Вероятно, наиболее изученными объектами с точки зрения характеристики их сложности являются одно- и двумерные строки или последовательности символов. Для таких объектов было предложено множество подходов для количественного определения или оценки сложности [3], [8], [10] — [18]. Однако внутренняя проблема любой меры сложности состоит в том, что существуют альтернативные способы восприятия и, следовательно, описания сложности, неизбежно ведущие к множеству различных мер сложности [19].Например, сложность Колмогорова [2], [3], [8], [20] основана на алгоритмической теории информации, рассматривающей объекты как отдельные строки символов, тогда как меры эффективной меры сложности (EMC) [16], превышения энтропия [21], прогнозная информация [22], термодинамическая глубина [17] или статистическая сложность [14] связывают объекты со случайными величинами и, следовательно, основаны на ансамбле или совокупности.
В контексте сетей были предложены меры сложности графов для исследования сложности химических графов, представляющих молекулы и химические соединения [23] — [25].Были разработаны различные типы мер сложности графов, которые можно в общих чертах разделить на теоретико-информационные и нефеоретико-информационные. Поскольку до сих пор в значительной степени неясно, какие структурные особенности сети следует подчеркивать, были разработаны иерархические подходы к химической сложности, состоящей из нескольких иерархических уровней молекулярной сложности. Одна из первых попыток была предпринята Берцем [26] для разработки иерархической модели, содержащей как топологические (т.е., разветвление, кольца, кратные связи) и нетопологические (размер молекулы, симметрия, функциональность, элементный состав) признаки; подробное обсуждение см. в [25]. Позже Бончев и Полански [27] развили эту систему и описали всю сложность химической системы с помощью векторного подхода. Компоненты этого вектора представляют различные характеристики сложности, например, размер системы, топологию графа, физическую природу, метрику системы и ее симметрию [27].
Одна из первых попыток была предпринята Берцем [26] для разработки иерархической модели, содержащей как топологические (т.е., разветвление, кольца, кратные связи) и нетопологические (размер молекулы, симметрия, функциональность, элементный состав) признаки; подробное обсуждение см. в [25]. Позже Бончев и Полански [27] развили эту систему и описали всю сложность химической системы с помощью векторного подхода. Компоненты этого вектора представляют различные характеристики сложности, например, размер системы, топологию графа, физическую природу, метрику системы и ее симметрию [27].
Также для общих сетей было предложено множество мер сетевой сложности [24], [28].Многие из них основаны на принципах теории информации [29] — [31]. Классическим, не теоретико-информационным подходом является так называемая комбинаторная сложность , введенная Миноли [32]. Эта мера представляет собой монотонно возрастающую функцию факторов, которые вносят вклад в сложность сети, например, количества вершин и ребер, степеней вершин, множества ребер, циклов, циклов и меток [33]. Другие методы основаны на определении конкретных подструктур в графах [24], [28].Также Константин и др. В [34] сложность графа определяется как количество содержащихся в нем остовных деревьев. Операторный подход был разработан Юкной [35], который определил сложность графа как минимальное количество операций объединения и пересечения, необходимых для получения всего набора его ребер, начиная с графов-звезд. Подходы к определению сложности графов, основанные на парадигме сложности Колмогорова [3], можно найти в [36], [37]. В частности, Бончев [37] сравнил колмогоровскую сложность графа с другими мерами и затронул вопрос, могут ли все эти методы обнаруживать ветвление в графах.
Основная цель данной статьи — представить сетевой показатель, называемый оценкой разнесения сети , и продемонстрировать, что этот показатель позволяет классифицировать сети в зависимости от их структурной сложности. В частности, мы демонстрируем, что показатель разнообразия позволяет отличать упорядоченные, случайные и сложные сети друг от друга. Кроме того, мы изучаем 16 дополнительных показателей сложности сети и обнаруживаем, что ни одна из этих мер не имеет аналогичных хороших возможностей категоризации в отношении структурной сложности сетей.В отличие от многих других мер, предложенных до сих пор, оценка сетевого разнообразия отличается по разным причинам. Во-первых, наша оценка мультипликативно состоит из четырех отдельных оценок, каждая из которых оценивает различные структурные свойства сети. Это означает, что наша общая оценка отражает структурное разнообразие сети. Абстрактно это можно рассматривать как измерение сложности сети. Во-вторых, наша оценка определяется для совокупности сетей, а не для отдельных сетей. Мы покажем, что это устраняет нежелательную двусмысленность, изначально присутствующую в мерах, основанных на отдельных сетях.Чтобы обеспечить практическое применение показателя сетевого разнообразия, мы предоставляем статистическую оценку для этого показателя, основанную на конечном числе сетей, отобранных из основной совокупности сетей.
В частности, мы демонстрируем, что показатель разнообразия позволяет отличать упорядоченные, случайные и сложные сети друг от друга. Кроме того, мы изучаем 16 дополнительных показателей сложности сети и обнаруживаем, что ни одна из этих мер не имеет аналогичных хороших возможностей категоризации в отношении структурной сложности сетей.В отличие от многих других мер, предложенных до сих пор, оценка сетевого разнообразия отличается по разным причинам. Во-первых, наша оценка мультипликативно состоит из четырех отдельных оценок, каждая из которых оценивает различные структурные свойства сети. Это означает, что наша общая оценка отражает структурное разнообразие сети. Абстрактно это можно рассматривать как измерение сложности сети. Во-вторых, наша оценка определяется для совокупности сетей, а не для отдельных сетей. Мы покажем, что это устраняет нежелательную двусмысленность, изначально присутствующую в мерах, основанных на отдельных сетях.Чтобы обеспечить практическое применение показателя сетевого разнообразия, мы предоставляем статистическую оценку для этого показателя, основанную на конечном числе сетей, отобранных из основной совокупности сетей.
Эта статья организована следующим образом. Поскольку определение структурной сложности сетей страдает от тех же проблем, что и для одномерных символьных строк, было предложено несколько эвристических критериев, которым должна соответствовать мера сложности [25], [27]. Чтобы прояснить, что мы подразумеваем под сложной сетью , мы приводим в разделе «Характеристика сложности сетей» описание этого, на которое мы опираемся в этой статье.Затем мы описываем 16 показателей сложности сети, используемых для нашего анализа, и характеризуем их вычислительную сложность. Чтобы представить меры сложности сети, используемые в этой статье, мы грубо разделим их на два класса: теоретико-информационные и нефеоретико-информационные меры. Ясно, что каждую группу можно разделить на подкатегории. Например, мы могли бы отнести класс чисто дистанционных мер и мер, основанных на собственных значениях, к категории мер, не относящихся к теории информации. Как известно, теоретико-информационные меры сложности графа [23], [38] основаны на выводе распределения вероятностей с учетом структурных особенностей графа. Точнее, так называемые меры, основанные на разбиениях, и меры, не основанные на разбиениях, могут быть получены с использованием энтропии Шеннона, см. [23], [39]. Другие меры энтропии графа, основанные на использовании подграф-отношений, можно найти в [28]. Не относящиеся к теории информации меры сложности в основном основаны на преобразовании инвариантов простых графов, таких как степени вершин и величины, основанные на расстоянии [40], в действительные числа [41], [42].Например, первый индекс Загреба [41], [42] преобразует степени вершин в положительную меру для характеристики структуры графа. Другой класс мер сложности, не относящихся к теории информации, основан на получении подграфов и последующем преобразовании их в меры, в конечном итоге приводящие к мере сложности графа, см. [28]. В разделе «Оценка сетевого разнообразия» мы определяем нашу меру и разъясняем концептуальные отличия от других подходов. В разделе результатов мы исследуем все 17 сетевых показателей для различных настроек и сравниваем их друг с другом.Статья завершается разделом «Заключение», в котором резюмируются полученные результаты.
Как известно, теоретико-информационные меры сложности графа [23], [38] основаны на выводе распределения вероятностей с учетом структурных особенностей графа. Точнее, так называемые меры, основанные на разбиениях, и меры, не основанные на разбиениях, могут быть получены с использованием энтропии Шеннона, см. [23], [39]. Другие меры энтропии графа, основанные на использовании подграф-отношений, можно найти в [28]. Не относящиеся к теории информации меры сложности в основном основаны на преобразовании инвариантов простых графов, таких как степени вершин и величины, основанные на расстоянии [40], в действительные числа [41], [42].Например, первый индекс Загреба [41], [42] преобразует степени вершин в положительную меру для характеристики структуры графа. Другой класс мер сложности, не относящихся к теории информации, основан на получении подграфов и последующем преобразовании их в меры, в конечном итоге приводящие к мере сложности графа, см. [28]. В разделе «Оценка сетевого разнообразия» мы определяем нашу меру и разъясняем концептуальные отличия от других подходов. В разделе результатов мы исследуем все 17 сетевых показателей для различных настроек и сравниваем их друг с другом.Статья завершается разделом «Заключение», в котором резюмируются полученные результаты.
Методы
В этом разделе мы, во-первых, даем характеристику сложности сетей, используемых в этой статье. Затем мы описываем 16 показателей сложности сети, которые мы используем в нашем анализе, и характеризуем их вычислительную сложность. После этого мы вводим новую меру сложности, которая называется оценка сетевого разнообразия (NDS), и даем мотивацию для ее определения.
Характеристика сложности сетей
Как указано во введении, до сих пор не существует общепринятого определения сложности, которое было бы применимо к общим объектам, включая сети. Однако обычно считается, что мера сложности должна позволять отличать сложные объекты от случайных и упорядоченных объектов. Для объектов, порождаемых физическим процессом, эта характеристика сложности была дана в [4], [19]. Однако аналогичные утверждения были сделаны и в отношении сложности биологических систем [43].Далее мы принимаем эту точку зрения. На рисунке 1А представлена визуализация этой характеристики в контексте сетей. На этом рисунке ось x соответствует одномерной переменной, которая представляет сети G из сетевого пространства, а ось y дает значение меры сложности. Здесь предполагается, что переменная q гладко представляет сети аналогичного типа. Вот почему определенные области оси x были помечены как упорядоченные, сложные или случайные.Конкретные примеры такой переменной — это Лэнгтон [44] для одномерных клеточных автоматов или средняя связность K в случайных логических сетях [45].
Для объектов, порождаемых физическим процессом, эта характеристика сложности была дана в [4], [19]. Однако аналогичные утверждения были сделаны и в отношении сложности биологических систем [43].Далее мы принимаем эту точку зрения. На рисунке 1А представлена визуализация этой характеристики в контексте сетей. На этом рисунке ось x соответствует одномерной переменной, которая представляет сети G из сетевого пространства, а ось y дает значение меры сложности. Здесь предполагается, что переменная q гладко представляет сети аналогичного типа. Вот почему определенные области оси x были помечены как упорядоченные, сложные или случайные.Конкретные примеры такой переменной — это Лэнгтон [44] для одномерных клеточных автоматов или средняя связность K в случайных логических сетях [45].
Важно прояснить связь между тремя различными объектами: сетью G , переменной q , представляющей сеть, и мерой сложности M . Сеть — это абстрактный объект, который обладает множеством различных свойств, например, количеством узлов, распределением степеней, средней длиной пути между всеми узлами, и это лишь некоторые из них.По этой причине сеть нелегко измерить с помощью одной переменной, потому что отображение,, обычно не является уникальным. Например, если мы отождествляемся с (глобальным) коэффициентом кластеризации сети G [46], то есть много сетей, которые имеют одинаковое значение q . По этой причине при отображении сети G на q значение q фактически представляет собой набор сетей, которые отображаются на одно и то же значение q , то есть с. Аналогичные аргументы справедливы, когда мы сопоставляем сеть со значением ее сложности, т.е.е.,. Также в этом случае обычно многие сети сопоставляются с одним и тем же значением сложности с. Интересно отметить, что после того, как сети были идентифицированы как сложные , случайные или упорядоченные , с использованием меры сложности M , объект q может служить в качестве меры сложности, если он демонстрирует свойство гладкости по отношению к базовым сетям. Здесь гладкость означает, что аналогичные сети приводят к аналогичным значениям q .Это свойство гладкости позволяет идентифицировать непрерывные области (интервалы) значений q , которые представляют определенные типы сетей, как показано на рис. 1A.
Здесь гладкость означает, что аналогичные сети приводят к аналогичным значениям q .Это свойство гладкости позволяет идентифицировать непрерывные области (интервалы) значений q , которые представляют определенные типы сетей, как показано на рис. 1A.
Конкретная проблема, которую мы хотим изучить в этой статье, отличается от вышеупомянутой. Вместо использования меры сложности M для категоризации сетей на сложные, случайные или упорядоченные группы, мы предполагаем, что такая категоризация для сетей уже известна. Из приведенного выше обсуждения мы знаем, что если мы найдем гладкую меру, представляющую наборы сетей, которые присваиваются аналогичным типам сетей, аналогичные значения q , тогда q могут служить мерой сложности.Это означает, что для сетей, которые помечены в соответствии с определенными категориями, к которым они принадлежат, и показателем q , можно количественно оценить качество такого показателя по отношению к данным ярлыкам сетей. Следовательно, используя знания о маркировке различных сетей, мы можем исследовать возможности категоризации меры q .
На рис. 1 B показано альтернативное поведение меры сложности в зависимости от сетей. В этом случае мы назвали значения по оси y «оценкой», а не мерой сложности, потому что здесь оценка для сложных сетей приводит не к максимально возможным значениям, а к промежуточным значениям.Однако преимущество такой оценки по сравнению с показателями, показанными на рис. 1A, состоит в том, что она позволяет различать все три типа сетей, сложные, упорядоченные и случайные сети, учитывая только оценку сетей. Следовательно, есть три непрерывных области значений оценки, которые позволяют однозначно различать три типа сетей. Возможны и полезны другие конфигурации, однако в дальнейшем мы основываем свой анализ на этой базовой характеристике сложности и применяем ее к сетям.Как показывают наши численные результаты, принципиальное поведение оценки, изображенное на рис. 1В, имеет практическое значение для нашего анализа (см. Рис. 8 и его обсуждение).
1В, имеет практическое значение для нашего анализа (см. Рис. 8 и его обсуждение).
Определение мер сложности
Далее мы даем краткое описание мер сложности, которые мы используем в нашем исследовании. Обозначим через G сеть, имеющую набор вершин V и набор ребер E . Количество вершин равно количеству ребер. В таблице 1 представлен обзор 16 используемых нами показателей сложности.
Теоретико-информационные меры сложности.
Для структурной характеристики сетей были разработаны различные энтропийные меры, определяющие их структурное информационное содержание [38]. Следующие меры основаны на энтропии Шеннона.
- Содержание топологической информации:
Одной из первых мер было введенное Рашевским [58] топологическое информационное содержание (1)
.Здесь обозначает количество топологически эквивалентных вершин в i -й вершинной орбите G , а k — количество различных орбит.является мерой симметрии в графах. Эта мера исчезает для полностью симметричного графа, такого как регулярные графы, и достигает своего максимального значения для асимметричных графов. Важно отметить, что Trucco [59] также исследовал эту меру, а Mowshowitz [56] обобщил ее для определения структурного информационного содержания графов и изучил их математические свойства [56], [60], [61].
Более общая мера сложности графа принадлежит Берцу и выражает полное структурное информационное содержание графа: (2)
X — произвольный инвариант графа, такой как его вершины, ребра, степени и т. Д.относится к его мощности. Например, если X соответствует вершинам сети, то соответствует количеству вершин. Если выбрать, то получим (3)
как особый случай.
- Индекс Бончева-Тринайстича:
Определяя взвешенные вероятностные схемы, можно обобщить классические меры Рашевского и Мовшовица [56], [58], см. 1. Его особая мера установлена в (4)
1. Его особая мера установлена в (4)
Этот показатель основан на индексе Винера [57], (5)
Обратите внимание, что индекс Винера — это сумма всех расстояний на графике G .Расстояния можно вычислить с помощью алгоритма Дейкстры или любого другого метода вычисления кратчайших путей в графе [62], [63]. Здесь — диаметр сети G , а — количество кратчайших путей длиной i .
- Теоретико-информационная мера сложности на основе информационных функционалов:
Следующая мера принадлежит к семейству мер энтропии графов, основанных на использовании информационных функционалов [39].Его специальным показателем является индекс ассоциации степень-степень, поскольку он основан на специальном информационном функционале, см. [52]. Функционал определяется формулой (6)
Подробное объяснение и определение можно найти в [52]. Индекс ассоциации степень-степень определяется формулой (7)
.— постоянная масштабирования. Обратите внимание, что это не основано на определении разбиений элементов графа в классическом смысле (например,), поскольку значения вероятности присваиваются каждой вершине G .
Для определения недиагональной сложности () [54], пусть будет корреляционной матрицей вершина-вершина, см. [54].обозначает количество всех соседей, имеющих степень всех вершин со степенью i [28]. обозначает максимальную степень G . Если определить [28] (8)
и (9)
можно определить как [28] (10)
- Чувствительность связующего дерева:
Следующая мера основана на определении подструктур в графах. Чувствительность остовного дерева [28] определяется формулой (11) с, и является упорядоченным списком всех k различных.- количество остовных деревьев в графе за вычетом количества остовных деревьев подграфа с удаленным ребром. Аналогично, мера различий чувствительности связующего дерева определяется как (12) с, где — упорядоченный список всех уникальных различий.
Аналогично, мера различий чувствительности связующего дерева определяется как (12) с, где — упорядоченный список всех уникальных различий.
Не-теоретико-информационные меры сложности.
Не относящиеся к теории информации меры сложности для сетей могут быть определены с помощью произвольных инвариантов графа, таких как расстояния между узлами или их степени. Далее мы описываем некоторые важные меры, которые уже использовались в различных дисциплинах.
Индекс Balaban J определяется как [42], [47] (13)
обозначает сумму расстояний от вершины до всех остальных вершин, т. Е. (14), тогда как D — это матрица расстояний, содержащая длины кратчайших путей между всеми вершинами, измеренная расстоянием Дейкстры [63], и является цикломатическим числом [64] .
Индекс сложности B — это более новая мера, разработанная Бончевым [24] 🙁 15)
где (16)
Здесь — степень вершины.
Latora et al. [49], [50] разработали меру, называемую сложностью эффективности графа G . Начиная с (17)
, выражающее среднее арифметическое всех обратных длин путей и (18)
Эффективность по сложности уступает (19)
В общем, меры, основанные на расстоянии, легко вычислить с полиномиальной временной сложностью [62]. Следовательно, были разработаны различные индексы, основанные на расстоянии, для характеристики сетей на основе их топологии [40], [65].Среднее отклонение расстояния, введенное Скоробогатовым и Добрыниным, определяется как [40], [42] 🙁 20)
где (21)
и (22)
- Нормализованная сложность кромок:
Нормализованная сложность ребер с использованием элементов матрицы смежности была введена Бончевым [24] 🙁 23)
где (24)
Здесь обозначает запись в i -й строке и j -м столбце соответствующей матрицы смежности A .
- Индекс связи Рандича:
Индекс связности Рандича [55] (25) успешно использовался в качестве индекса ветвления. Кроме того, R был тщательно исследован, например, границы и другие экстремальные свойства были исследованы междисциплинарным образом [66].
Кроме того, R был тщательно исследован, например, границы и другие экстремальные свойства были исследованы междисциплинарным образом [66].
Одним из первых декскрипторов структурных графов был индекс Винера [57], (26)
обозначает кратчайшее расстояние между и.
Классический индекс, основанный на степени вершины, — это первый индекс Загреба [41], [42], определяемый как (27)
— это просто сумма степеней вершины G .
Вычислительная сложность
Вычисление сложности сетей может потребовать больших вычислительных ресурсов, и многие алгоритмы даже являются NP-полными [68]. Например, определение группы автоморфизмов общего графа для вычисления меры энтропии графа требует вычислений, поскольку вычислительная сложность может быть экспоненциальной [69].Напротив, временная сложность некоторых теоретико-информационных мер сложности графов, таких как B , OdC, является полиномиальной, см. [70]. В частности, временная сложность индекса Бончева-Тринайстича и индекса связи степень-степень такова, что нам нужно вычислить все кратчайшие пути между всеми вершинами в графе, ведущими к. Аналогичные утверждения [28], [70] для временной сложности J могут быть получены, когда необходимо вычислить полную матрицу расстояний.Простые топологические сетевые меры, такие как индекс Винера и Рэндича, также обладают полиномиальной временной сложностью, поскольку их вычисление основывается на матричных вычислениях, основанных на инвариантах графов.
Временная сложность определения нулей (собственных значений) [71] многочленов графа [51], таких как характеристический многочлен или многочлен расстояния, также является полиномиальной. Например, используя матрицу смежности для вычисления характеристического полинома графа, мы получаем его собственные значения за полиномиальное время.Исходя из этого, можно эффективно вычислить такие меры, как энергия графика E и энергия Лапласа LE .
Оценка сетевого разнообразия
Далее мы определяем сетевую меру, которую мы называем оценкой разнесения сети (NDS). Наша оценка основана на 4 переменных: (30) (31) (32) (33)
Здесь M — количество модулей в сети G и n — количество вершин этой сети. Вектор содержит размер модулей, т.е.е., дает размер i-го модуля, который соответствует количеству узлов в этом модуле. Для идентификации модулей в сети мы используем метод под названием Walktrap [72], который находит модули на основе случайных блужданий, подобных [73], [74]. Преимущество этого метода перед многими другими заключается в его эффективной вычислительной сложности, определяемой выражением (e: количество ребер, n: количество вершин). Вектор в уравнении. 32 представляет собственные значения матрицы Лапласа L сети G [75], компоненты которой определяются формулой (34)
Здесь степень узла i в G .Наконец, и соответствуют количеству мотивов размера 3 и 4, найденных в сети G [76]. Это означает, что такое количество различных мотивов можно найти в G , имеющем i узлов.
На основе вышеуказанных четырех переменных мы определяем оценку индивидуального разнообразия для сети G по формуле (35)
Мы называем этот показатель индивидуальным показателем разнообразия , потому что он может быть рассчитан для одной сети G . Оценка индивидуального разнообразия оценивает одну сеть G и принимает значения в.На основе этого мы определяем оценку разнесения сети (NDS), для совокупности сетей как (36)
. Здесь обозначает совокупность сетей, принадлежащих одной сетевой модели, и представляет собой плотность вероятности для этой совокупности. Например, это может соответствовать модели случайной сети, созданной с помощью модели Эрдеша-Рейни [77], [78]. Или это может быть набор всех безмасштабных сетей, сгенерированных с помощью алгоритма предпочтительного присоединения [79], [80]. Или совокупность может включать все сети с одинаковой степенью, например.g., решетка с периодическими граничными условиями. Это означает, что совокупность сетей может быть определена либо случайным процессом, который генерирует сети в совокупности, либо структурными свойствами самих сетей.
Или совокупность может включать все сети с одинаковой степенью, например.g., решетка с периодическими граничными условиями. Это означает, что совокупность сетей может быть определена либо случайным процессом, который генерирует сети в совокупности, либо структурными свойствами самих сетей.
Чтобы получить приближение меры, которая может быть применена к конечному набору сетей, мы определяем оценку разнесения сети для выборки размера из совокупности с помощью оценщика, (37)
Предполагая, что сети S независимо выбираются из совокупности, чем, согласно центральной предельной теореме [81], (38)
Для наших численных исследований мы используем оценку, приведенную в формуле.37.
Оценка разнообразия представляет идею о том, что сеть является многомерным объектом. В частности, мы считаем важными 4 переменные и. Переменная предоставляет информацию о плотности модулей в сети. Для сложных сетей мы ожидаем найти больше модулей, чем для случайных сетей, потому что модули являются выражением общего организационного принципа сети. Переменная — это показатель роста мотивов в сети. Из численных результатов мы заметили, что упорядоченные сети имеют наивысшее значение, сложная сеть — промежуточные, а случайные сети — самые низкие значения.Переменная аналогична значению CV (коэффициент вариации), которое измеряет изменчивость размеров сети по отношению к среднему размеру модуля. Ожидается, что случайные сети будут иметь низкую изменчивость размеров модулей, но также и низкий средний размер модуля, тогда как сложные сети должны иметь более высокую изменчивость размеров модулей, но также и более высокий средний размер модуля. Переменная аналогична, но для собственных значений матрицы Лапласа L . Мы изучили множество комбинаций этих 4 и других переменных и в результате численных исследований обнаружили, что индивидуальная плотность в уравнении.35 приводит к наилучшему разделению случайных, сложных и упорядоченных сетей.
Мотивация для оценки сетевого разнообразия.
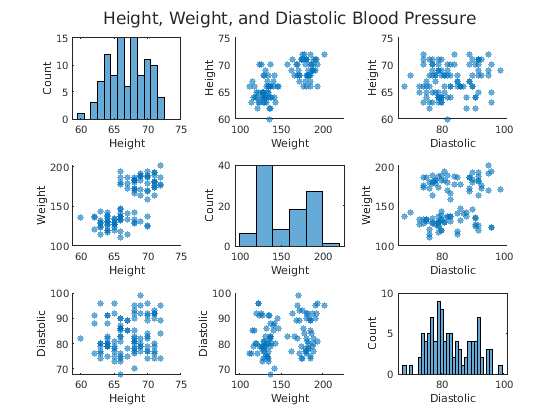
Рациональное значение, лежащее в основе нашей меры, основано на следующих наблюдениях. Во-первых, исследования сложности различных типов объектов, например одномерных цепочек, привели к введению большого количества различных мер сложности. Однако до сих пор нет единого мнения о том, что мера right входит в число введенных.Что касается сетей, мы сталкиваемся с аналогичной ситуацией, которая потенциально может быть еще более серьезной. По этой причине мы предлагаем комплексную меру, которая основана не только на оценке одного структурного принципа , но и на комбинации нескольких. Следовательно, их комбинаторное использование снижает потребность в каждой отдельной мере для представления правой меры сложности . В разделе результатов мы численно продемонстрируем, что такая комплексная мера на самом деле приводит к очень хорошим результатам.
Вторая причина, побудившая нас ввести нашу меру, лучше всего описывается следующей иллюстрацией. Предположим, кто-то определяет сети как «случайные», если они были сгенерированы с помощью модели случайных сетей, предложенной Эрдеш-Рейни и Гилбертом [77], [78], и как «сложные», когда они были созданы с помощью алгоритма предпочтительного присоединения. [79], [80]. Тогда существует отличная от нуля вероятность сгенерировать случайную сеть с моделью случайной сети, которая также является сложной.Однако это противоречит интуиции. Давайте рассмотрим пример для этой проблемы. Предположим, сеть была сгенерирована с использованием случайной сетевой модели, а вторая сеть была сгенерирована с помощью алгоритма предпочтительного присоединения. Тогда с определенной вероятностью (со смыслом) выполняется, потому что случайная сетевая модель, в принципе, может генерировать все возможные сетевые структуры. Точнее, если неориентированная сеть содержит e ребер (обозначенных) и n вершин, то она содержит недостающие ребра (не ребра).Это означает, что вероятность, w , для модели случайной сети сгенерировать конкретную сеть с ребрами e , равна (39)
Здесь — вероятность наличия e ребер и вероятность наличия не ребер. Это означает, что присвоение значения сложности отдельным сетям приводит к потере уникальной связи между сложностью сети и базовой сетевой моделью, которая сгенерировала эту сеть. Это показано на рис.2 A. На этом рисунке w соответствует вероятности того, что модель случайной сети генерирует сложную сеть. Исходя из значения сложности сети в правой части рисунка, можно сделать вывод, что она была создана либо с помощью случайной сетевой модели, либо с помощью сложной сетевой модели. Для простоты мы использовали в приведенном выше объяснении только две сетевые модели, однако расширение на большее количество моделей является прямым, но делает объяснения более трудоемкими.Должно быть ясно, что в таком расширенном сценарии вероятность неоднозначности между сложностью отдельных сетей и моделей создания сетей даже усиливается.
Это означает, что присвоение значения сложности отдельным сетям приводит к потере уникальной связи между сложностью сети и базовой сетевой моделью, которая сгенерировала эту сеть. Это показано на рис.2 A. На этом рисунке w соответствует вероятности того, что модель случайной сети генерирует сложную сеть. Исходя из значения сложности сети в правой части рисунка, можно сделать вывод, что она была создана либо с помощью случайной сетевой модели, либо с помощью сложной сетевой модели. Для простоты мы использовали в приведенном выше объяснении только две сетевые модели, однако расширение на большее количество моделей является прямым, но делает объяснения более трудоемкими.Должно быть ясно, что в таком расширенном сценарии вероятность неоднозначности между сложностью отдельных сетей и моделей создания сетей даже усиливается.
Рисунок 2. Связь между сетевой моделью, сетями и мерой сложности, оценивающей сложность отдельных сетей (A), совокупности сетей (B) или выборки сетей (C).
https://doi.org/10.1371/journal.pone.0034523.g002
Чтобы избежать этой проблемы, мы основываем нашу сетевую оценку по принципу, изображенному на рис.2 B. В связи с тем, что сложность оценивается для популяции сети , созданной сетевой моделью, нет никакой путаницы в отношении базовой сетевой модели, которая генерировала совокупность, потому что мера сложности может полагаться на информацию предоставляется всем населением, а не только по его частям. На практике мы аппроксимируем такую меру совокупности, используя конечную выборку сетей, как показано на рис.2 C.Для конечной выборки, состоящей из сетей S , также существует ненулевая вероятность того, что возникнет неоднозначная связь между сложность и лежащая в основе сетевая модель, которая сгенерировала образец сети, визуализированная на рис.2 C. Однако эта вероятность является лишь по сравнению с w для меры сложности, основанной на одной сети. В пределе эта вероятность стремится к нулю, и модель C становится моделью B для любого. Следовательно, использование выборки размером S снижает вероятность двусмысленности, ведущей к неправильной классификации, в раз. Например, если и размер выборки только, чем этот фактор уже есть.
Следовательно, использование выборки размером S снижает вероятность двусмысленности, ведущей к неправильной классификации, в раз. Например, если и размер выборки только, чем этот фактор уже есть.
Мы хотели бы подчеркнуть, что приведенные выше объяснения служат мотивацией нашего подхода, а не численным анализом наиболее общей мыслимой ситуации.В этом отношении вероятность w , приведенная в формуле. 39 необходимо адаптировать для более общих ситуаций. Однако, независимо от его точного значения, w всегда будет больше нуля, и приведенное выше обсуждение принципа плавно переносится на более сложные условия. В следующем разделе мы проводим численный анализ большого количества различных сетей.
Результаты
Мы начинаем наш анализ с исследования статистической изменчивости 16 показателей сложности сети, перечисленных в Табл.1. На рис. 3 показаны результаты для 100 сетей, сгенерированных с помощью модели случайных сетей [77], [78] для параметров и. Здесь n соответствует количеству узлов в сети, а параметр — это вероятность, с которой два узла соединены ребром. Каждая гистограмма показывает результат для одного показателя сложности, как указано в названии в легенде. Ось x соответствует значению соответствующей меры сложности, а ось y дает частоту наблюдаемых значений.Важно отметить, что, несмотря на то, что все случайные сети были сгенерированы для одних и тех же сетевых параметров, n и, результирующие меры сложности не дают идентичных результатов, а колеблются. Мы повторили этот анализ для разных параметров модели случайной сети, а также для разных типов сетей, т.е. для сложных сетей. Для всех изученных случаев были получены качественно похожие результаты. Это обнаруживает общий концептуальный недостаток всех этих сетевых мер, поскольку ни одна из мер не рассматривается как случайная величина.Однако из-за того, что сеть отбирается из базовой совокупности, эта сеть различается по структуре и, следовательно, также и сетевая мера, как показано на рис. 3. Это означает, что игнорирование этого факта контрпродуктивно и приводит к потерям. интерпретируемости этих сетевых мер, как будет продемонстрировано позже в этом разделе (см. рис. 7). Как объясняется в разделе «Оценка сетевого разнообразия», случайная сетевая модель в принципе способна генерировать все возможные типы сетей, включая упорядоченные и сложные сети, однако только с определенной вероятностью.В связи с тем, что все меры оценивают только одну сеть, которая была случайным образом выбрана из базовой совокупности сетевой модели, выбранная сеть передает изменчивость сетевых структур совокупности самой сетевой мере.
3. Это означает, что игнорирование этого факта контрпродуктивно и приводит к потерям. интерпретируемости этих сетевых мер, как будет продемонстрировано позже в этом разделе (см. рис. 7). Как объясняется в разделе «Оценка сетевого разнообразия», случайная сетевая модель в принципе способна генерировать все возможные типы сетей, включая упорядоченные и сложные сети, однако только с определенной вероятностью.В связи с тем, что все меры оценивают только одну сеть, которая была случайным образом выбрана из базовой совокупности сетевой модели, выбранная сеть передает изменчивость сетевых структур совокупности самой сетевой мере.
На рис. 4–5 показаны результаты для двух различных сетевых моделей и влияние параметров модели на 16 показателей сложности. На рис. 4 показаны результаты для модели случайной сети с вероятностью соединения между узлами ( x -ось).На рис. 5 показаны результаты для сетевой модели «маленького мира» [82] для вероятности переназначения ( x -ось). На этих рисунках среднее значение и стандартное отклонение меры сложности (ось y) показаны в зависимости от параметра модели ( x -ось).
Рис. 4 демонстрирует, что среди 16 показателей сложности можно наблюдать четыре качественно различных типа поведения. Четыре наблюдаемых поведения: (1) монотонное увеличение значения сложности (сложностьIndexB, эффективность, энергия, lapEnergy, randic, sTreeSens, tInfoContent, zagreb1), (2) монотонное уменьшение значения сложности (infoTheoGCM), (3 ) возрастающие значения сложности с последующим уменьшением значений (bonchev2, mDistDev, wiener), (4) уменьшение значений сложности с последующим увеличением значений (balabanJ, nEdgeComplexity, недиагональ).Это указывает на то, что разные сетевые меры имеют совершенно разные характеристики из-за разных структурных особенностей сети, которую они захватывают. Кроме того, мы наблюдаем, что все меры, кроме infoTheoGCM, приводят к неперекрывающимся значениям для разных параметров модели, что означает, что разные значения приводят к существенно разным значениям соответствующих значений сложности. Это важно отметить, поскольку все сети, сгенерированные с помощью модели случайной сети для различных значений, являются случайными сетями.
Это важно отметить, поскольку все сети, сгенерированные с помощью модели случайной сети для различных значений, являются случайными сетями.
Результаты для сетевой модели малого мира, показанные на рис. 5, принципиально отличаются от результатов, показанных на рис. 4, потому что для разных значений мы получаем разные типы сетей. В частности, мы получаем упорядоченные (), сложные () и случайные сети (). Это отличается от результатов для модели случайной сети, потому что разные параметры модели всегда приводят к случайной сети, тогда как для сетевой модели малого мира разные параметры модели приводят к другому типу сети.Среди 16 сетевых показателей 5 демонстрируют дискриминационное поведение по отношению к трем различным типам сетей (balabanJ, сложностьIndexB, energy, mDistDev и sTreeSens). Это означает, что эти 5 показателей показывают для сложных сетей () заметно разные значения, чем для упорядоченных и случайных сетей.
На рис. 6 показаны результаты о влиянии размера сети n в диапазоне от 100 до 500 узлов на показатели сложности. Поскольку тип сети не меняется для другого размера сети, в идеале ожидали бы постоянные значения сетевых мер для всех различных размеров сети.Единственные меры, которые являются приблизительно постоянными, — это недиагональные и sTreeSens, потому что их средние значения сложности не сильно меняются, если принять во внимание стандартное отклонение меры. На все остальные меры существенно влияет размер сетей. Это намекает на то, что размер сети является важным параметром. Чтобы упростить следующий анализ, мы изучаем только сети фиксированного размера.
До сих пор мы изучали только отдельные сетевые модели для множества различных параметров, от которых эти модели зависят.Теперь мы исследуем смесь различных сетевых моделей. В частности, мы генерируем набор, состоящий из 1500 сетей, каждая из которых имеет вершины. Этот набор состоит из 200 упорядоченных сетей, 600 случайных сетей и 700 сложных сетей. Набор сложных сетей сам по себе представляет собой смесь безмасштабных сетей с различными параметрами мощности модели предпочтительного присоединения и сетей малого мира с вероятностью переподключения. Для набора случайных сетей мы использовали разные параметры соединения вершин ребром, а именно,.Кроме того, мы сгенерировали случайные сети с помощью модели маленького мира, установив вероятность переназначения равной 1,0. Это означает, что результирующий набор сетей неоднороден по отношению к генерации используемых сетей. Среднее количество ребер этих наборов упорядоченных, случайных и сложных сетей составляет 200 для каждого типа сети, а их стандартное отклонение составляет 109,43 и 60. Тот же набор данных позже будет использоваться для изучения показателя сетевого разнообразия (см. Рис. . 8).
Набор сложных сетей сам по себе представляет собой смесь безмасштабных сетей с различными параметрами мощности модели предпочтительного присоединения и сетей малого мира с вероятностью переподключения. Для набора случайных сетей мы использовали разные параметры соединения вершин ребром, а именно,.Кроме того, мы сгенерировали случайные сети с помощью модели маленького мира, установив вероятность переназначения равной 1,0. Это означает, что результирующий набор сетей неоднороден по отношению к генерации используемых сетей. Среднее количество ребер этих наборов упорядоченных, случайных и сложных сетей составляет 200 для каждого типа сети, а их стандартное отклонение составляет 109,43 и 60. Тот же набор данных позже будет использоваться для изучения показателя сетевого разнообразия (см. Рис. . 8).
Применение 16 мер сложности приводит к результатам, показанным на рис.7. Эти рисунки показывают плотность вероятности значений сложности ( y — ось) в зависимости от значений сложности сетей ( x — ось). Три разных цвета соответствуют упорядоченным (красный), сложным (фиолетовый) и случайным (зеленый) сетям. Идеальное поведение меры сложности, которую мы хотели бы наблюдать, — это разделение трех разных типов сетей, что означает, что плотность значений сложности для упорядоченных, сложных и случайных сетей должна лишь незначительно перекрываться, чтобы обеспечить значимую категоризацию трех типы сетей.Рассматривая полученные численные результаты на рис. 7 с этой точки зрения, мы обнаруживаем, что только недиагональная сложность позволяет, по крайней мере, до определенной степени, отделить три типа сетей друг от друга. Плотности всех других мер вообще не разделяются. Проблема с плотностью недиагональной сложности заключается не только в том, что она бимодальна для сложных сетей, но и в том, что все еще существует значительное перекрытие сложных (фиолетовый) и случайных сетей (красный).
Рисунок 8.Плотность оценки разнообразия для упорядоченных (красный), сложных (фиолетовый) и случайных (зеленый) сетей.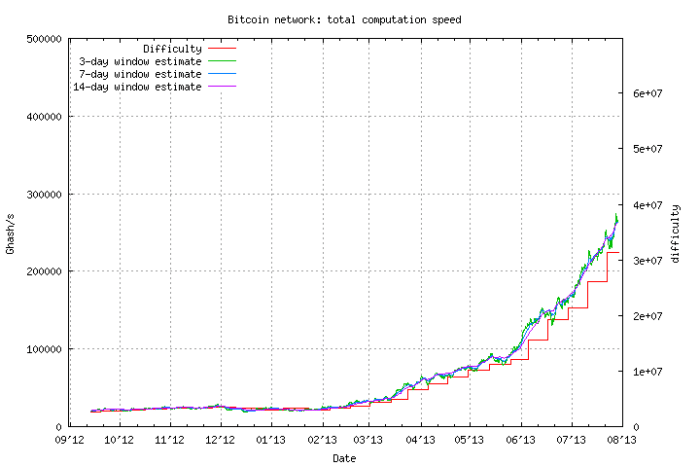
В первой строке показаны результаты для сетей с узлами, а во второй строке — для узлов. Четыре столбца соответствуют четырем размерам выборки.
https://doi.org/10.1371/journal.pone.0034523.g008
Затем мы исследуем поведение показателя сетевого разнообразия, приведенного в уравнении. 37. В верхнем ряду на рис. 8 показаны результаты применения оценки разнообразия к.Поскольку наша оценка сложности зависит от размера выборки S , четыре столбца на рис. 8 соответствуют четырем разным размерам выборки (). Следовательно, количество различных сетей, используемых для этих четырех случаев, равно количеству сетей. Мы хотели бы подчеркнуть, что для, оценка дает наихудшее возможное приближение для оценки плотности . Этот случай не включен, чтобы предположить, что это потенциальный выбор S , вместо этого он включен, чтобы продемонстрировать силу эффекта популяции для значений.По этой причине мы подчеркиваем отличие данного случая от других, обрамляя первый столбец на рис. 8 синим прямоугольником, чтобы указать, что это не подразумевается в качестве предлагаемого значения для размера выборки.
Из рис. 8 видно, что с увеличением значений размера выборки S три типа сетей — упорядоченные сети (красный), сложные сети (фиолетовый) и случайные сети (зеленый), соответственно, их плотности становятся все больше и больше. отделены друг от друга по желанию.Но даже для размера выборки результаты для оценки разнообразия улучшаются по сравнению с недиагональной сложностью, которая была лучшим показателем из всех 16 сетевых показателей. Во второй строке на рис. 8 показан аналогичный анализ, однако, для сетей с узлами, для которых мы сгенерировали другой набор сетей, содержащих сети. Ибо мы наблюдаем еще более четкое различие трех типов сетей, которые идеально отделяются друг от друга. Мы хотели бы подчеркнуть, что из-за характера показателя сетевого разнообразия, который основан на численности населения, сравнение с любым из 16 сетевых показателей является неравномерным, поскольку ни на один из этих показателей не может повлиять размер выборки S .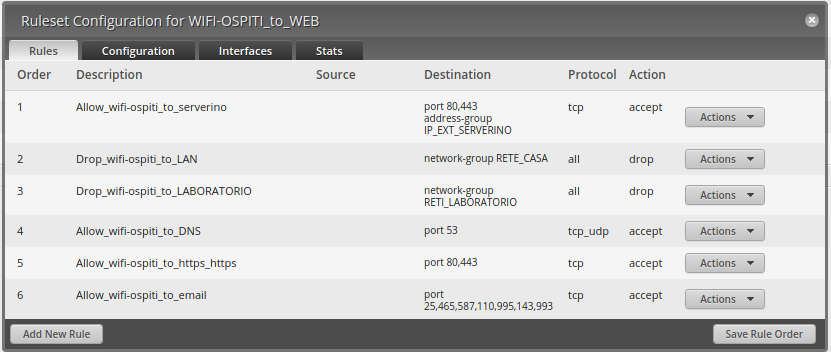 С другой стороны, образец сетей размером S содержит ценную информацию, которая может быть использована для увеличения различающих способностей меры, как показано на рис. 8. Это свидетельствует о том, что концептуальная идея измерения на основе совокупности, предложенный в этой статье, повышает эффективность меры для разделения сетей из разных категорий.
С другой стороны, образец сетей размером S содержит ценную информацию, которая может быть использована для увеличения различающих способностей меры, как показано на рис. 8. Это свидетельствует о том, что концептуальная идея измерения на основе совокупности, предложенный в этой статье, повышает эффективность меры для разделения сетей из разных категорий.
В качестве предостережения мы хотели бы подчеркнуть, что различающая способность показателя разнообразия составляет , не только из-за его популяционного характера, а из-за комбинации его популяционного характера и индивидуального разнообразия балла « (см.35), на котором основано. Из рис. 8 можно узнать о влиянии размера выборки, но он не дает информации о влиянии показателя индивидуального разнообразия . По этой причине мы исследовали влияние показателя индивидуального разнообразия , изменив его определение. Например, используя только подмножество четырех переменных, на которых основано (см. Уравнения 30–33), мы обнаружили, что популяционная версия такой меры фактически не приводит к различению различных типов сетей.Следовательно, только комбинация соответствующей оценки индивидуального разнообразия с популяционным подходом приводит к благоприятным характеристикам оценки разнообразия.
В разделе «Характеристика сложности сетей» мы дали характеристику сложности. Связь между этой характеристикой, представленной на рис. 1, и нашими результатами на рис. 8 задается кумулятивной функцией распределения (CDF) [81] плотностей на рис. 8. В качестве примера мы показываем CDF для и .Следовательно, оценка ( y — ось) на рис. 1 может быть идентифицирована с помощью кумулятивной функции распределения плотности вероятности оценки разнообразия.
Наконец, мы показываем на рис. 9 влияние размера выборки S на средний балл индивидуального разнообразия, соответствующий для сетей большого размера. Эти результаты показывают, что это среднее значение в значительной степени постоянное для различных значений размера выборки S , демонстрируя, что несмещенная оценка [83], заданная формулой. 37 дает хорошие оценки на практике даже для небольших выборок. Кроме того, этот рисунок демонстрирует, что очень маленькие размеры выборки использовать не рекомендуется, поскольку ожидаемая изменчивость оценок довольно велика.
37 дает хорошие оценки на практике даже для небольших выборок. Кроме того, этот рисунок демонстрирует, что очень маленькие размеры выборки использовать не рекомендуется, поскольку ожидаемая изменчивость оценок довольно велика.
Приложение для реальных сетей
Наконец, мы применяем оценку сетевого разнообразия к четырем реальным сетям. Мы используем две социальные сети, представляющие сети соавторства между учеными, работающими в области физики высоких энергий (hep,) [84] и сетевой науки (net,) [85], технологической сети, представляющей энергосистему западных штатов США (power, ) [82] и биологическая сеть, представляющая белок-белковые взаимодействия в Helicobacter pylori (hpylo,) [86], бактерии, обитающей в желудке.Число в скобках относится к числу узлов в гигантском связном компоненте этих сетей, который мы используем в дальнейшем для нашего анализа.
Поскольку у нас есть только одна сеть для каждой из этих четырех сетей, к которой мы можем применить оценку сетевого разнообразия, мы используем следующее свойство сложности. Обычно предполагается, что одним из аспектов сложности объекта является наличие иерархической организационной структуры [10], [87], [88]. Это означает, что сложен не только сам объект в целом, но и достаточно крупные его компоненты.Для нашего анализа мы используем это, случайным образом выбирая подсети из сети G . Это означает, что мы получаем выборку из S сетей из одной сети путем случайного генерирования подсетей с n вершинами из G . Таким образом, мы получаем выборку сетей, в то время как каждая сеть была выбрана из сети G , то есть (40)
, который аппроксимирует выборку из базовой сетевой модели. Практически мы генерируем подсети путем случайного блуждания.Начиная с начальной вершины, которая случайным образом выбирается из всех вершин сети, подсеть определяется первыми уникальными вершинами, посещенными случайным блужданием. Это позволяет, во-первых, сгенерировать выборку сетей из сетевой модели, хотя доступна только одна сеть.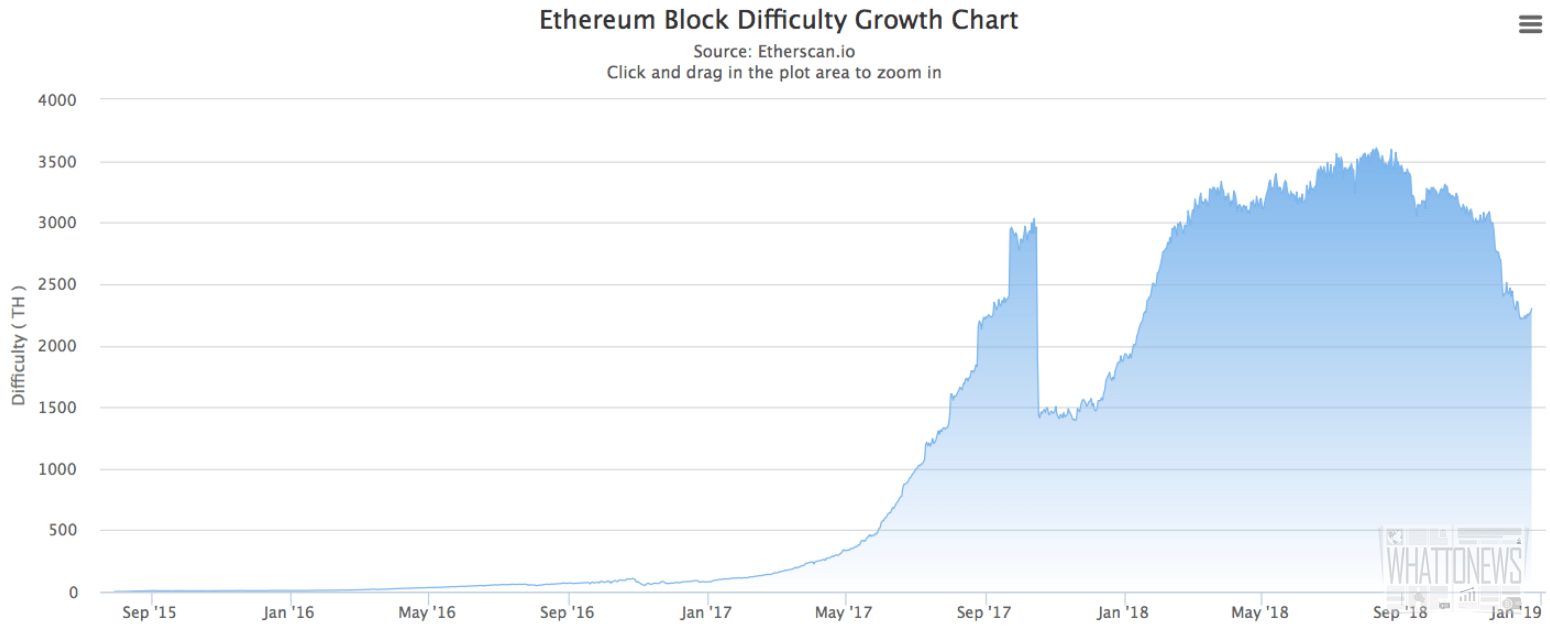 Во-вторых, размер каждой сети может быть установлен на фиксированное значение n . Это позволяет сравнивать сети с разным размером, потому что все сети в выборках имеют одинаковое количество вершин.
Во-вторых, размер каждой сети может быть установлен на фиксированное значение n . Это позволяет сравнивать сети с разным размером, потому что все сети в выборках имеют одинаковое количество вершин.
На рис. 10 показаны результаты для этих четырех сетей. Кроме того, мы включили результаты для случайных сетей (красная кривая), сгенерированных с помощью модели Эрдеша-Рейни. Ось x дает размер подсетей: n . Размер выборки для этого анализа составлял, и мы усреднили все результаты по 100 независимым выборкам. Это означает, что на рис. 10 мы проанализировали все сети. В целом, можно видеть, что случайные сети приводят к самым низким значениям оценки плотности, а для подсетей большого размера расстояния между отдельными сетями в основном постоянны.Это указывает на то, что для исследуемых сетей размер подсетей достаточно велик, чтобы охватить сложность всей сети.
Обсуждение
В этой статье мы исследовали поведение 17 сетевых показателей в отношении их способности систематически классифицировать структурную сложность сетей. Наш анализ показывает, что построение сетевой меры таким образом, чтобы она усредняла выборку сетей из совокупности, значительно расширяет ее возможности по классификации различных типов сетей.Из наших численных результатов следует, что это свойство усреднения оценки разнообразия является ключевым для достижения идеального разделения трех различных типов сетей, упорядоченных, сложных и случайных сетей, которые мы исследовали в нашем анализе. Ключевым моментом здесь является то, что это свойство усреднения снижает важность поиска правильного показателя сети , который точно определяет количественно то, что подразумевается под структурной сложностью сети. В связи с тем, что мера сложности правой сети неизвестна, мы определили показатель разнообразия, мультипликативно составленный из четырех индивидуальных оценок, каждая из которых оценивает различные структурные свойства сети.Следовательно, комбинация показателя сетевого разнообразия, который фокусируется не на одном структурном свойстве сети, а на нескольких свойствах, вместе с усреднением по выборке сетей из совокупности, приводит к сетевому показателю, который выглядит хорошо. принят к предложенной задаче. Мы хотели бы подчеркнуть, что существуют другие меры сложности, которые также включают основную совокупность в определении меры [14], [16], [17], [21], [22], однако все эти меры сложности были изучены только в контексте последовательностей символов.
принят к предложенной задаче. Мы хотели бы подчеркнуть, что существуют другие меры сложности, которые также включают основную совокупность в определении меры [14], [16], [17], [21], [22], однако все эти меры сложности были изучены только в контексте последовательностей символов.
Теоретически усреднение по выборке сетей из генеральной совокупности не только очень благотворно влияет на числовую категоризацию различных типов сетей, но также устраняет концептуальную неоднозначность, присутствующую во всех измерениях, которые оценивают только отдельные сети с уважение к их сложности. Как обсуждалось в разделе «Методы», случайная сетевая модель также способна генерировать сложные сети. Следовательно, теоретически можно генерировать различные типы сетей с помощью случайной сетевой модели.Это неизбежно приводит к неправильной классификации сетей. Напротив, оценка разнообразия, предложенная в этой статье, уменьшает эту неоднозначность в раз, при этом S является размером выборки.
Категоризация сетей в зависимости от их структурной сложности представляет интерес не только с теоретической, но и с практической точки зрения. Например, в молекулярной биологии обычно предполагается, что молекулярные взаимодействия между белками и молекулами создают биологическую функцию клеток и повышают фенотипический облик организмов.В связи с тем, что графическое представление таких молекулярных взаимодействий дается генными сетями, было предложено сравнить эти сети структурно, чтобы идентифицировать аберрации молекулярных функций [89] — [91]. В качестве расширения вышеупомянутого подхода кажется естественным оценивать структурную сложность генных сетей, например, регуляторных сетей, чтобы различать разные стадии сложных заболеваний, таких как рак или сердечно-сосудистые заболевания, друг от друга. Например, данные экспрессии генов из микрочипов ДНК можно использовать для вывода регуляторной сети для каждого пациента, который принадлежит к определенной стадии или степени заболевания. Тогда такую степень заболевания можно рассматривать как категорию, из которой отбираются пациенты и их соответствующие сети. Таким образом, наша сетевая оценка может применяться для сравнения пациентов с разными стадиями или степенями заболевания друг с другом. Учитывая темпы роста данных в молекулярной биологии благодаря постоянным технологическим инновациям, можно ожидать, что такие наборы данных будут доступны в ближайшем будущем. Другие потенциальные области применения — это категоризация финансовых сетей [92] — [94] или нейронных сетей [95], [96].
Тогда такую степень заболевания можно рассматривать как категорию, из которой отбираются пациенты и их соответствующие сети. Таким образом, наша сетевая оценка может применяться для сравнения пациентов с разными стадиями или степенями заболевания друг с другом. Учитывая темпы роста данных в молекулярной биологии благодаря постоянным технологическим инновациям, можно ожидать, что такие наборы данных будут доступны в ближайшем будущем. Другие потенциальные области применения — это категоризация финансовых сетей [92] — [94] или нейронных сетей [95], [96].
Благодарности
Мы хотели бы поблагодарить Рикардо де Матос Симоэс, Шайлеша Трипати и Джона Квакенбуша за плодотворные обсуждения. Для численного моделирования мы использовали R [97] и пакет QuACN [98].
Вклад авторов
Задумал и спроектировал эксперименты: FES MD. Проведенные эксперименты: ФЭС МД. Проанализированы данные: ФЭС к.м.н. Предоставленные реактивы / материалы / инструменты анализа: ФЭС МД. Написал доклад: ФЭС МД.
Ссылки
- 1.Бар-Ям Ю. (1997) Динамика сложных систем. Книги Персея.
- 2. Чайтин Г. (1966) О длине программ для вычисления конечных двоичных последовательностей. Журнал ACM. С. 547–569.
- 3. Колмогоров А.Н. (1965) Три подхода к количественному определению «информации». Проблемы передачи информации 1: 1–7.
- 4. Лопес-Руиса Р., Мансиниб Х., Кальбет Х (1995) Статистическая мера сложности. Physics Letters A 209: 321–326.
- 5. Николис Г., Пригожин И. (1989) Изучение сложности. Фримен.
- 6. Прокопенко М., Боскетти Ф, Райан А. (2009) Теоретико-информационный учебник по сложности, самоорганизации и возникновению. Сложность 15: 11–28.
- 7. Шустер Х (2002) Сложные адаптивные системы. Скатор Верлаг.
- 8.
Solomonoff R (1960) Предварительный отчет по общей теории индуктивного вывода. Технический отчет V-131, Zator Co.
 , Кембридж, штат Массачусетс.
, Кембридж, штат Массачусетс. - 9. Вольфрам С. (1983) Статистическая механика клеточных автоматов. Phys Rev E 55: 601–644.
- 10. Бадий Р., Полит А. (1997) Сложность: иерархические структуры и масштабирование в физике. Издательство Кембриджского университета, Кембридж.
- 11. Беннет C (1988) Логическая глубина и физическая сложность. Херкен Р., редактор Универсальной машины Тьюринга — обзор за полвека, Oxford University Press. С. 227–257.
- 12.Кратчфилд Дж. П., Янг К. (1989) Вывод статистической сложности. Phys Rev Lett 63: 105–108.
- 13. Emmert-Streib F (2010) Исследовательский анализ пространственно-временных паттернов клеточных автоматов путем кластерной сжимаемости. Physical Review E 81: 026103.
- 14. Эммерт-Стрейб Ф (2010) Статистическая сложность: сочетание сложности Колмогорова с ансамблевым подходом. PLoS ONE 5: e12256.
- 15. Гелл-Манн М., Ллойд С. (1998) Информационные меры, эффективная сложность и полная информация.Сложность 2: 44–52.
- 16. Грассбергер П. (1986) К количественной теории самопроизведенной сложности. Int J Theor Phys 25: 907–938.
- 17. Lloyd S, Pagels H (1988) Сложность как термодинамическая глубина. Анналы физики 188: 186–213.
- 18. Зурек В., редактор. (1990) Сложность, энтропия и физика информации. Эддисон-Уэсли, Редвуд-Сити.
- 19. Грассбергер П. (1989) Проблемы количественной оценки самопроизвольной сложности.Helvetica Physica Acta 62: 489–511.
- 20. Ли М., Витаньи П. (1997) Введение в сложность Колмогорова и ее приложения. Springer.
- 21. Кратчфилд Дж., Паккард Н. (1983) Символическая динамика шумного хаоса. Physica D 7: 201–223.
- 22. Бялек В., Неменман И., Тишби Н. (2001) Предсказуемость, сложность и обучение. Нейронные вычисления 13: 2409–2463.
- 23.
Бончев Д.
 (1983) Теоретико-информационные показатели для характеристики химических структур.Research Studies Press, Чичестер.
(1983) Теоретико-информационные показатели для характеристики химических структур.Research Studies Press, Чичестер. - 24. Бончев Д., Руврей Д.Х. (2005) Сложность в химии, биологии и экологии. Математическая и вычислительная химия. Springer. Нью-Йорк, штат Нью-Йорк, США.
- 25. Янежич Д., Милежевич А., Николич С., Тринайстич Н. (2009) Топологическая сложность молекул. Мейерс Р., редактор, Энциклопедия сложности и системных наук, Springer, том 5. С. 9210–9224.
- 26. Бертц Ш. (1983) О сложности графов и молекул.Bull Math Biol 45: 849–855.
- 27. Бончев Д., Полянский О.Е. (1987) О топологической сложности химических систем. King RB, Rouvray DH, редакторы, теория графов и топология, Elsevier. С. 125–158. Амстердам, Нидерланды.
- 28. Ким Дж., Вильгельм Т. (2008) Что такое сложный граф? Physica A 387: 2637–2652.
- 29. Dancoff SM, Quastler H (1953) Информационное содержание и частота ошибок живых существ. Квастлер Х., редактор, Essays on the Use of Information Theory in Biology, University of Illinois Press.С. 263–274.
- 30. Линшиц Х. (1953) Информационное содержание элемента батареи. Квастлер Х., редактор, Essays on the Use of Information Theory in Biology, University of Illinois Press. Урбана, штат Иллинойс, США.
- 31. Моровиц Х. (1953) Некоторые соображения порядка-беспорядка в живых системах. Bull Math Biophys 17: 81–86.
- 32. Миноли Д. (1975) Комбинаторная сложность графов. Атти Accad Naz Lincei, VIII Ser, Rend, Cl Sci Fis Mat Nat 59: 651–661.
- 33. Бончев Д. (2003) Сложность в химии. Введение и основы. Тейлор и Фрэнсис. Бока-Ратон, Флорида, США.
- 34. Константин Г (1990) Сложность графа и матрица лапласа в блокированных экспериментах. Линейная и полилинейная алгебра 28: 49–56.
- 35.
Юкна С. (2006) О сложности графа. Расческа Probab Comput 15: 855–876.

- 36. Ли М., Витаньи П. (1997) Введение в сложность Колмогорова и ее приложения.Springer.
- 37. Бончев Д. (1995) Информация Колмогорова, энтропия Шеннона и топологическая сложность молекул. Bulg Chem Commun 28: 567–582.
- 38. Демер М., Мовшовиц А. (2011) История мер энтропии графов. Информационные науки 1: 57–78.
- 39. Демер М. (2008) Обработка информации в сложных сетях: энтропия графа и информационные функционалы. Appl Math Comput 201: 82–94.
- 40. Скоробогатов В.А., Добрынин А.А. (1988) Метрический анализ графов.Commun Math Comp Chem 23: 105–155.
- 41. Диудеа М.В., Гутман И., Янтски Л. (2001) Молекулярная топология. Нова Паблишинг. Нью-Йорк, штат Нью-Йорк, США.
- 42. Todeschini R, Consonni V, Mannhold R (2002) Справочник по молекулярным дескрипторам. Вайнхайм: Wiley-VCH.
- 43. Адами С (2002) Что такое сложность? BioEssays 24: 1085–1094.
- 44. Лэнгтон C (1990) Вычисления на краю choas: фазовые переходы и эмерджентные вычисления.Physica D 42: 12–37.
- 45. Рибейро А.С., Кауфман С.А., Ллойд-Прайс Дж., Самуэльссон Б., Socolar JES (2008) Взаимная информация в случайных булевых моделях регуляторных сетей. Phys Rev E 77: 011901.
- 46. Ньюман М (2010) Сети: Введение. Оксфорд: Издательство Оксфордского университета.
- 47. Балабан А.Т. (1982) Высоко различительный топологический индекс, основанный на расстоянии. ChemPhysLett 89: 399–404.
- 48. Бончев Д., Тринайстич Н. (1977) Теория информации, матрица расстояний и молекулярное ветвление.J. Chem Phys 67: 4517–4533.
- 49. Латора В., Маркиори М. (2001) Эффективное поведение сетей малого мира. Phys Rev Lett 87: 198701.
- 50.
Latora V, MarchioriM (2003) Экономическое поведение малого мира во взвешенных сетях. Европейский физический журнал B Condensed Matter 32: 249–263.

- 51. Гутман I (1991) Полиномы в теории графов. Бончев Д., Руврей Д.Х., редакторы, Химическая теория графов. Введение и основы, Abacus Press.pp133–176. Нью-Йорк, штат Нью-Йорк, США.
- 52. Демер М., Эммерт-Стрейб Ф, Цой Ю., Вармуза К. (2011) Количественная оценка структурной сложности графов: информационные меры в математической химии. Путц М., редактор Quantum Frontiers of Atoms and Molecules, Nova Publishing. С. 479–498.
- 53. Гутман И., Чжоу Б. (2006) Лапласова энергия графа. Линейная алгебра и ее приложения 414: 29–37.
- 54. Клауссен Дж. К. (2007) Характеристика сетей недиагональной сложностью.Physica A 365–373: 321–354.
- 55. Randić M (1975) О характеристике молекулярного разветвления. J Amer Chem Soc 97: 6609–6615.
- 56. Mowshowitz A (1968) Энтропия и сложность графов I: индекс относительной сложности графа. Bull Math Biophys 30: 175–204.
- 57. Винер Х. (1947) Структурное определение точек кипения парафинов. Журнал Американского химического общества 69: 17–20.
- 58. Рашевский Н. (1955) Жизнь, теория информации и топология.Bull Math Biophys 17: 229–235.
- 59. Trucco E (1956) Заметка об информативности графиков. Bull Math Biol 18: 129–135.
- 60. Mowshowitz A (1968) Энтропия и сложность графов II: информационное содержание орграфов и бесконечных графов. Bull Math Biophys 30: 225–240.
- 61. Mowshowitz A (1968) Энтропия и сложность графов III: Графы с заданным информационным содержанием. Bull Math Biophys 30: 387–414.
- 62. Кормен Т.Х., Лейзерсон К.Э., Ривест Р.Л. (1990) Введение в алгоритмы. MIT Press.
- 63. Дейкстра Э. (1959) Заметка о двух проблемах, связанных с графами. Numerische Math 1: 269–271.
- 64.
Балабан А.Т., Балабан Т.С. (1991) Новые вершинные инварианты и топологические индексы химических графов, основанные на информации о расстояниях.
 J Math Chem 8: 383–397.
J Math Chem 8: 383–397. - 65. Бакли Ф., Харари Ф. (1990) Расстояние в графах.Издательство Эддисон Уэсли.
- 66. Ли X, Гутман I (2006) Математические аспекты дескрипторов молекулярной структуры типа Рандича. Монографии по математической химии. Крагуевацкий университет и научный факультет Крагуеваца.
- 67. Демер М., Мюллер Л., Грабер А. (2010) Новые основанные на полиномах молекулярные дескрипторы с низкой вырожденностью. PLoS ONE 5:
- 68. Гэри М.Р., Джонсон Д.С. (1979) Компьютеры и несговорчивость: Руководство по теории неполноты NPC.Серия книг по математическим наукам. В. Х. Фриман.
- 69. Mowshowitz A, Mitsou V (2009) Энтропия, орбиты и спектры графов. Демер М., Эммерт-Стрейб Ф., редакторы, Анализ сложных сетей: от биологии до лингвистики, Wiley-VCH. С. 1–22.
- 70. Девиллерс Дж., Балабан А.Т. (1999) Топологические индексы и связанные дескрипторы в QSAR и QSPR. Издательство Gordon and Breach Science. Амстердам, Нидерланды.
- 71. Саган Х (1989) Граничные задачи и задачи на собственные значения в математической физике.Dover Publications.
- 72. Pons P, LatapyM (2005) Вычислительные сообщества в больших сетях с использованием случайных блужданий. Yolum p, Güngör T, Gürgen F, Özturan C, редакторы, Computer and Information Sciences — ISCIS 2005, Springer Berlin / Heidelberg, volume 3733 of Lecture Notes in Computer Science. С. 284–293.
- 73. Ван Донген С. (2000) Кластеризация графов с помощью потокового моделирования. Кандидат наук. докторская диссертация, Центры математики и информатики (CWI), Утрехтский университет.
- 74. Зив Э., Миддендорф М, Виггинс Ч. (2005) Теоретико-информационный подход к модульности сети. Phys Rev. E 71: 046117.
- 75. Чанг ФРК (1997) Теория спектральных графов. Американское математическое общество.
- 76.
Майло Р.
 , Шен-Орр С., Ицковиц С., Каштан Н., Чкловский Д. и др. (2002) Сетевые мотивы: простые строительные блоки сложных сетей. Наука 298: 824–7.
, Шен-Орр С., Ицковиц С., Каштан Н., Чкловский Д. и др. (2002) Сетевые мотивы: простые строительные блоки сложных сетей. Наука 298: 824–7. - 77. Эрдеш П., Реньи А. (1959) О случайных графах.I. Математические публикации 6: 290–297.
- 78. Гилберт Э. Н. (1959) Случайные графы. Анналы математической статистики 20: 1141–1144.
- 79. Альберт Р., Барабаши А. (2002) Статистическая механика сложных сетей. Издание современной физики 74: 47.
- 80. Барабаши А.Л., Альберт Р. (1999) Появление масштабирования в случайных сетях. Наука 206: 509–512.
- 81. Феллер В. (1968) Введение в теорию вероятностей и ее приложения.1. Джон Уайли и сыновья.
- 82. Уоттс Д., Строгац С. (1998) Коллективная динамика сетей «маленького мира». Природа 393: 440–442.
- 83. Lehman E, Casella G (1999) Теория точечного оценивания. Нью-Йорк: Спрингер.
- 84. NewmanMEJ (2001) Структура сетей научного сотрудничества. Слушания Национальной академии наук Соединенных Штатов Америки 98: 404–409.
- 85. Ньюман MEJ (2006) Нахождение структуры сообщества в сетях с использованием собственных векторов матриц.Phys Rev E 74: 036104.
- 86. Xenarios I, Rice DW, Salwinski L, Baron MK, Marcotte EM, et al. (2000) DIP: База данных взаимодействующих белков. Nucl Acids Res 28: 289–291.
- 87. Ceccatto HA, Huberman BA (1988) Сложность иерархических систем. Physica Scripta 37: 145
- 88. Равас Э., Сомера А.Л., Монгру Д.А., Олтвай З.Н., Барабаши А.Л. (2002) Иерархическая организация модульности в метаболических сетях. Наука 297: 1551–1555.
- 89. Emmert-Streib F (2007) Синдром хронической усталости: сравнительный анализ путей. Журнал вычислительной биологии 14: 961–972.
- 90.
Эммерт-Стрейб Ф., Глазко Г. (2011) Анализ данных экспрессии: расшифровка функциональных строительных блоков сложных заболеваний.
 PLoS Computational Biology 7: e1002053.
PLoS Computational Biology 7: e1002053. - 91. Schadt E (2009) Молекулярные сети как датчики и драйверы распространенных заболеваний человека. Природа 461: 218–223.
- 92. Богинский В., Бутенко С., Пардалос П. (2005) Статистический анализ финансовых сетей. Вычислительная статистика и анализ данных 48: 431–443.
- 93. Эммерт-Стрейб Ф., Демер М. (2010) Определение критических финансовых сетей DJIA: на пути к сетевому индексу. Сложность 16: 24–33.
- 94. Эммерт-Стрейб Ф., Демер М. (2010) Влияние временной шкалы на построение финансовых сетей. PLoS ONE 5: e12884.
- 95.Kaiser M, Hilgetag CC, Kötter R (2010) Иерархия и динамика нейронных сетей. Границы нейроинформатики 4:
- 96. Sporns O (2011) Сети мозга. Кембридж, Массачусетс: MIT Press.
- 97. Основная группа разработчиков R (2008 г.) R: Язык и среда для статистических вычислений. R Фонд статистических вычислений, Вена, Австрия. ISBN 3-1-07-0.
- 98. Мюллер Л.А., Куглер К.Г., Дандер А., Грабер А., Демер М. (2010) QuACN — пакет R для количественного анализа сложных биологических сетей.Биоинформатика.
Сравнение методов для сравнения сетей
В этом разделе мы выбираем некоторые из ранее описанных методов, а также определяем и проводим тесты на синтетических сетях для оценки производительности каждого метода. Наконец, мы проиллюстрируем приложение на реальных сетевых данных. Как правило, мы рассматриваем только те методы, для которых исходный / исполняемый код бесплатно предоставляется авторами метода (подробности используемых кодов находятся в файле дополнительной информации, разд.S2), чтобы достоверно протестировать каждый метод с точки зрения правильности (исключение составляют базовый и спектральный методы, требующие вычисления простых расстояний, которые были непосредственно закодированы нами).
В частности, среди методов KNC мы включили:
Различие матриц смежности (с нормами Евклида, Манхэттена, Канберры и Жаккара) в качестве базового подхода;
DeltaCon, благодаря своим описанным выше желаемым свойствам, и с целью тестирования нетривиального метода KNC.
 Мы также протестировали реализацию для направленных сетей.
Мы также протестировали реализацию для направленных сетей.
Среди методов UNC мы выбрали:
(абсолютную) разность коэффициента кластеризации и диаметра по мере приближения базовой линии;
Для методов на основе выравнивания, MI-GRAAL, который позволяет извлекать дополнительную информацию из отображения узлов;
Для методов, основанных на графах, GCD-11 и DCGD-129. Первый предназначен для неориентированных сетей, и было доказано, что он очень эффективен при различении синтетических сетей с различными топологиями 19 .Вторая — это направленная версия GCD-11, за исключением того, что, в отличие от GCD-11, DGCD-129 не исключает избыточных орбит;
Для спектральных методов подход Уилсона и Чжу 37 : мы определяем три расстояния, вычисляя евклидово расстояние между спектрами матриц смежности, лапласианов и симметричных нормализованных лапласианов 52 (SNL) (подход Гера и др. . 38 было отброшено, так как код не был доступен).
NetLSD, основанный на решении динамического («теплового») уравнения;
Наконец, портретное расхождение, которое, естественно, может иметь дело с ненаправленными и направленными сетями.
Исходный / исполняемый код недоступен для Cut Distance и Persistent Homology. Байесовский метод был исключен, поскольку прямое сравнение с другими подходами невозможно из-за его принципиально иной природы. Наконец, GRAFENE был исключен, потому что, несмотря на то, что он определен для общих сетей, исполняемый файл, предоставленный авторами, сильно зависит от предметной области, т.е.е., это требует биологически обоснованного определения сети.
Мы суммируем в таблице 1 методы, выбранные для тестирования, классифицированные по типу сети, которой они могут управлять, и по характеру самого метода. В столбце UNC мы обычно вставляем «Глобальную статистику» во все строки, хотя конкретно используемая статистика может зависеть от типа сети. Мы отмечаем, что тесты, которые мы проводили на синтетических сетях, ограничиваются невзвешенным случаем: определение подходящих сетей с взвешенными тестами и адекватных стратегий тестирования для них — сложная и деликатная задача, выходящая за рамки настоящей работы.Обратите внимание, что в невзвешенном (двоичном) случае расстояния MAN и CAN фактически дают тот же результат, что и (квадрат) расстояния EUC; таким образом, три расстояния фактически одинаковы, и в анализе будет учитываться только расстояние EUC.
Мы отмечаем, что тесты, которые мы проводили на синтетических сетях, ограничиваются невзвешенным случаем: определение подходящих сетей с взвешенными тестами и адекватных стратегий тестирования для них — сложная и деликатная задача, выходящая за рамки настоящей работы.Обратите внимание, что в невзвешенном (двоичном) случае расстояния MAN и CAN фактически дают тот же результат, что и (квадрат) расстояния EUC; таким образом, три расстояния фактически одинаковы, и в анализе будет учитываться только расстояние EUC.
Тесты возмущений
Мы выполняем последовательные возмущения, начиная с исходного графа, и измеряем после каждого возмущения расстояние полученного графа от исходного.Это нацелено на проверку того, в какой степени рассматриваемое сетевое расстояние имеет «регулярное» поведение. Фактически, мы ожидаем, что какое бы расстояние мы ни использовали, оно должно стремиться к нулю, когда возмущения стремятся к нулю, т.е. расстояние между очень похожими графиками мало; кроме того, расстояние должно монотонно увеличиваться с увеличением количества возмущений, а это означает, что флуктуации, если они есть, должны быть очень ограничены. Кроме того, для возмущений, которые имеют тенденцию к рандомизации графа (см. Ниже), расстояние должно достигать некоторого асимптотического значения после большого числа возмущений, потому что, когда граф становится полностью рандомизированным, он остается таким для любых дальнейших возмущений (см. 16 для формального обсуждения свойств мер подобия).
Рассматриваются следующие типы возмущений:
Удаление ( pREM-test ): связанная пара узлов выбирается равномерно случайным образом и ребро удаляется (плотность графа уменьшается).
Добавление ( pADD-test ): пара неподключенных узлов выбирается равномерно случайным образом и добавляется ребро (плотность графа увеличивается).

Случайное переключение ( pRSW-test ): объединяет два предыдущих: пара подключенных узлов выбирается равномерно случайным образом и ребро удаляется; затем случайным образом выбирается несвязанная пара узлов и добавляется ребро (плотность графа не меняется).
Переключение с сохранением степени ( pDSW-test ): два ребра выбираются равномерно случайным образом и меняются местами: если мы выберем ( i , j ) и ( u , v ) , мы удаляем их и вставляем новые ребра ( i , v ) и ( j , u ), если они еще не существуют (плотность графа и распределение степеней не меняются).
Кроме того, для направленных сетей:
Изменение направления ( pDIR-test ): подключенная пара узлов выбирается равномерно случайным образом, а направление ребер меняется на противоположное (плотность графа не меняется).
Мы рассматриваем два семейства сетей, т. Е. Ненаправленные и направленные, и три модели для каждого семейства, т. Е. Erdös-Rényi (ER) 53 , Barabási-Albert (BA) 54 и Lancichinetti-Fortunato- Radicchi (LFR) 55,56 (см. Исх. 16 для альтернативных предложений синтетических тестовых сетей для методов сравнения). Три модели, которые хорошо известны и широко используются в качестве испытательных стендов в различных задачах сетевой науки 2 , имеют возрастающую структурную сложность. В неориентированном случае ER-сеть 53 строится путем задания количества узлов и ссылок, а затем путем случайного назначения ссылок парам узлов, выбранным равномерно случайным образом. Это дает сеть с почти однородным распределением степеней, т.е.е., все узлы статистически эквивалентны и имеют небольшие колебания около средней степени. В сети BA 54 , с другой стороны, несколько узлов с очень высокой степенью сосуществуют с большинством узлов средней / малой степени, что приводит к сильно неоднородному (степенному) распределению степеней, которое встречается в ряде наборов данных из реального мира. Сети LFR 55,56 добавляют еще один уровень сложности, а именно модульную структуру: сеть разделена на сообщества, которые представляют собой подграфы с большой внутренней плотностью, но слабо связаны с другими сообществами, причем не только степенью узлов, но и размеры сообществ распределены по степенному закону, чтобы имитировать особенности, обычно встречающиеся в реальных данных.Три модели, первоначально разработанные для неориентированных сетей, были обобщены для направленных случаев (подробности о создании неориентированных и направленных сетей см. В файле дополнительной информации, раздел S3).
Сети LFR 55,56 добавляют еще один уровень сложности, а именно модульную структуру: сеть разделена на сообщества, которые представляют собой подграфы с большой внутренней плотностью, но слабо связаны с другими сообществами, причем не только степенью узлов, но и размеры сообществ распределены по степенному закону, чтобы имитировать особенности, обычно встречающиеся в реальных данных.Три модели, первоначально разработанные для неориентированных сетей, были обобщены для направленных случаев (подробности о создании неориентированных и направленных сетей см. В файле дополнительной информации, раздел S3).
Для каждой пары семейство / модель мы создаем два графа с 1000 узлами соответственно с плотностью 0,01 и 0,05. В каждой сети мы выполняем 10 различных повторений 1000 последовательных возмущений указанных выше типов. Для неориентированного и направленного случаев, соответственно, мы тестируем методы в первой и второй строке таблицы 1.Для «Глобальной статистики» мы используем коэффициент кластеризации и диаметр для ненаправленных сетей, а диаметр только для направленных сетей. Для плотности 0,05 и для всех направленных сетей мы исключаем MI-GRAAL из анализа, поскольку он оказывается слишком тяжелым в вычислительном отношении.
На рисунках 2 и 3 представлены результаты, полученные в ненаправленных сетях с плотностью 0,01 (см. Файл дополнительной информации, рисунки S1 и S2, для плотности 0,05). Мы замечаем, что практически все расстояния имеют «регулярное» поведение в рассмотренном выше смысле.Единственное примечательное исключение — это расстояние по диаметру, которое остается нулевым при широком диапазоне возмущений для большинства сетевых моделей, таким образом, оказывается неадекватным в качестве сетевого расстояния. Полосы уверенности в целом узкие, за исключением MI-GRAAL и GCD-11, которые колеблются сильнее. В некоторых случаях расстояния имеют тенденцию к насыщению — это особенно заметно в тестах переключения ( pRSW-test и pDSW-test ). В целом, эти результаты означают, что все расстояния четко определены и могут быть правильно использованы для сравнения — за исключением диаметра, который поэтому не будет учитываться в остальной части.
В целом, эти результаты означают, что все расстояния четко определены и могут быть правильно использованы для сравнения — за исключением диаметра, который поэтому не будет учитываться в остальной части.
: результаты тестов Removal ( pREM-test ) и Addition ( pADD-test ) для 12 дистанций и 3 ненаправленных моделей ER, BA, LFR (плотность 0,01). Сплошные (пунктирные) линии — это средние (± 3 стандартных) значения, полученные за 10 повторений историй возмущений.
Рисунок 3Испытания на возмущения: результаты Случайное переключение ( pRSW-test ) и Сохранение степени переключения ( pDSW-test ) тестов для 12 расстояний и 3 ненаправленных моделей ER, BA , LFR (плотность 0.01). Сплошные (пунктирные) линии — это средние (± 3 стандартных) значения, полученные за 10 повторений историй возмущений.
В то же время тесты показывают различное поведение для двух классов дистанций KNC и UNC (Таблица 1). Расстояния KNC оказываются практически нечувствительными к сетевой модели и даже к типу возмущения: на этих расстояниях возмущение действует одинаково во всех рассмотренных моделях. В этом нет ничего неожиданного: например, EUC просто измеряет (квадратный корень из) числа ребер, которые были добавлены, удалены или переключены, не обращая внимания на топологию, в которой происходят эти изменения: очень слабая характеристика эффектов возмущений.
Расстояния UNC, напротив, показывают совершенно разные значения и закономерности для разных моделей и возмущений. Три спектральных расстояния ведут себя по-разному от одного теста к другому. Тенденция линейна в pADD-test и pREM-test и не зависит от сетевой модели, в то время как для pRSW-test и pDSW-test расстояние определенно больше для сетей LFR почти во всех случаях. Это поведение отражает более высокую чувствительность сетей LFR к случайному переналадке из-за прогрессирующего разрушения встроенной структуры сообщества за счет удаления границ внутри сообществ и создания межобщинных связей.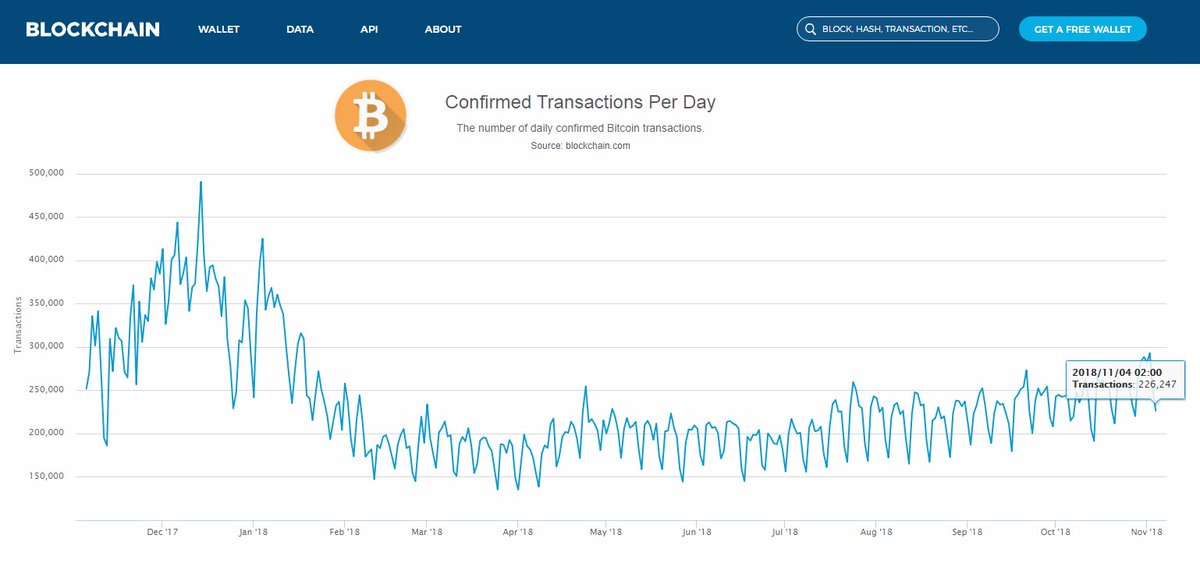 Действительно, такое же поведение демонстрируют коэффициент кластеризации и расстояние NetLSD. С другой стороны, pRSW-test влияет и на сети BA, по крайней мере, на некоторых расстояниях, потому что концентраторы легко теряют соединения. Примечательно, что на ER-сети слабо влияет случайное изменение схемы обоих типов, если оно измеряется спектральными расстояниями: случайное изменение схемы дает, конечно, разные графы, но структурно эквивалентные исходному.
Действительно, такое же поведение демонстрируют коэффициент кластеризации и расстояние NetLSD. С другой стороны, pRSW-test влияет и на сети BA, по крайней мере, на некоторых расстояниях, потому что концентраторы легко теряют соединения. Примечательно, что на ER-сети слабо влияет случайное изменение схемы обоих типов, если оно измеряется спектральными расстояниями: случайное изменение схемы дает, конечно, разные графы, но структурно эквивалентные исходному.
Переходя к последним расстояниям UNC, мы замечаем сравнительно большую изменчивость GCD-11.PDIV, с другой стороны, имеет своеобразное поведение: расстояние резко увеличивается при самых первых возмущениях, затем оно либо увеличивается дальше, но медленнее, либо сразу насыщается. Последнее относится, например, к моделям ER и BA в рамках pDSW-test : при случайном изменении схемы топология ER дает эквивалентные графы, которые почти одинаково удалены от исходного, но, что интересно, то же самое происходит и со структурой BA: мы утверждаем, что после pDSW-теста шагов распределение кратчайших путей почти одинаково для всех возмущенных графов, так что расстояние PDIV становится постоянным.
Расстояние MI-GRAAL отличается от всех остальных расстояний. Как отмечалось выше, доверительные интервалы показывают большую изменчивость. В некоторых крайних случаях (например, pREM-test и pDSW-test на графиках LFR или pADD-test и pDSW-test на графиках ER) доверительный интервал охватывает почти все [0, 1], а именно, несколько возмущений могут привести к графу, очевидно равному или полностью отличному от исходного, в зависимости от того, какие ребра возмущены.Такое неприятное поведение, вероятно, связано с большой чувствительностью к возмущениям локальных (узловых) особенностей. Напомним, что расстояние MI-GRAAL строит карту между наиболее похожими узлами сравниваемых сетей. Возмущения вызывают различия в характеристиках отдельных узлов, то есть в степени, коэффициенте кластеризации и центральности между узлами, которые могут скрывать и искажать правильное соответствие узлов. Кстати, ER-сети кажутся наиболее страдающими, по-видимому, потому, что узлы слабо охарактеризованы.
Кстати, ER-сети кажутся наиболее страдающими, по-видимому, потому, что узлы слабо охарактеризованы.
Наконец, на рис. 4 представлены результаты теста изменения направления ( pDIR-test ) в направленных сетях с плотностью 0,01 (см. Файл дополнительной информации, рис. S3 – S5, для плотности 0,05). Опять же, по тем же причинам, что и выше, простейшие расстояния (EUC и JAC) демонстрируют поведение, которое очень регулярно и нечувствительно к сетевой модели. Опять же, расстояние по диаметру имеет патологическое поведение, и от него в любом случае следует отказаться. Что проявляется в оставшихся двух расстояниях UNC, с другой стороны, так это их сильная чувствительность в случае сетей BA, где (см. Панели DGCD-129 и PDIV) даже первые несколько возмущений приводят к большим расстояниям.Чтобы объяснить этот эффект, следует подчеркнуть, что в наших направленных сетях BA по своей конструкции концентраторы представляют собой узлы, имеющие систематически большую начальную степень, в то время как исходящая степень однородно распределена (см. Файл дополнительной информации, раздел S3, для получения подробной информации о построение направленных сетей). Оказывается, нескольких изменений в направлениях ребер достаточно, чтобы резко изменить количество и тип графлетов (DGCD-129) и структуру кратчайших путей (PDIV). Такая высокая чувствительность может быть проблемой в некоторых приложениях, хотя она, безусловно, усиливается конкретной структурой наших тестовых сетей.
Рисунок 4Испытания на возмущения: результаты теста Изменение направления ( pDIR-test ) для 6 дистанций (см. Таблицу 1, MI-GRAAL исключен из соображений вычислений) и трех направленных моделей ER, BA , LFR (плотность 0,01). Сплошные (пунктирные) линии — это средние (± 3 стандартных) значения, полученные за 10 повторений историй возмущений.
Тесты кластеризации
В этом разделе предлагается несколько тестов, направленных на оценку эффективности каждого метода распознавания и группирования сетей с одинаковыми структурными особенностями, т.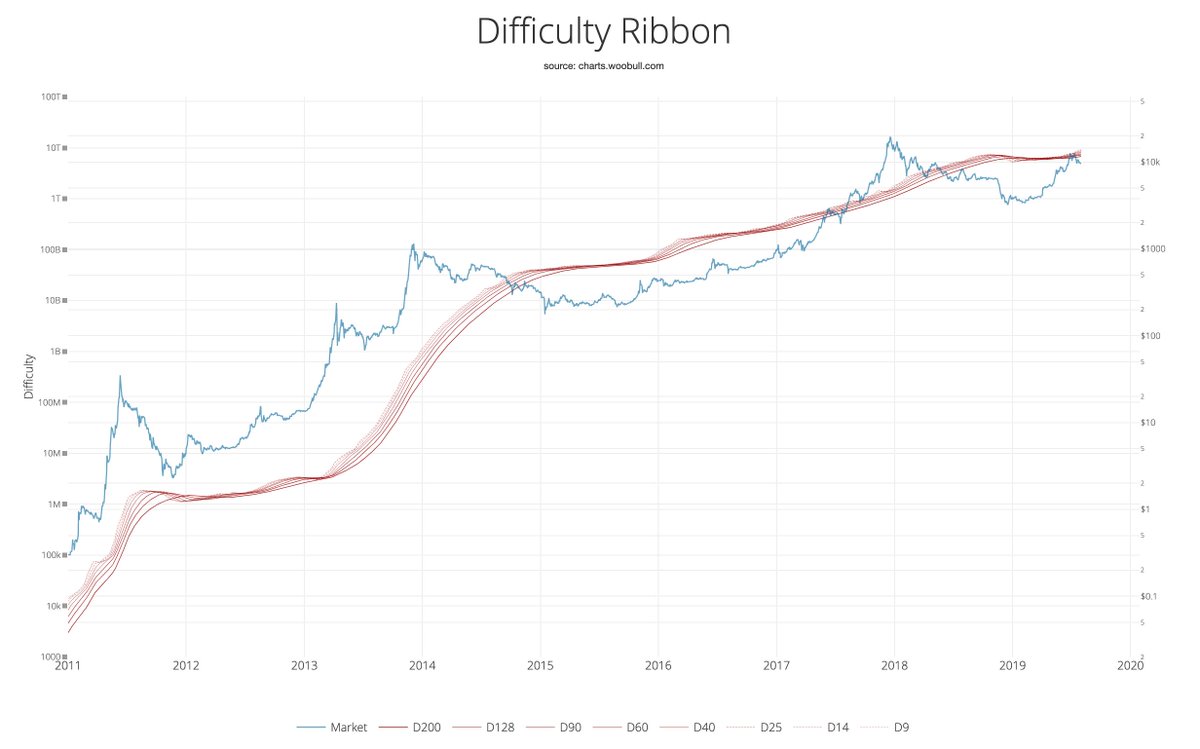 е.е., произошла от той же модели. Другими словами, чтобы обеспечить хорошую производительность, метод должен иметь возможность назначать небольшое расстояние сетевым парам, исходящим из одной и той же модели, но большое расстояние парам, исходящим из разных моделей. Мы применяем типичный подход для тестирования производительности методов, работающих в неконтролируемой среде, т. Е. Моделируя контролируемые сценарии, в которых группы (или, как в этом случае, сетевые модели) известны, затем выполняем алгоритмы, как в случае неконтролируемого вмешательства, наконец, проверка их способности правильно определять группы, происходящие из разных моделей.Обратите внимание, что для этой задачи подходят только методы UNC, поскольку мы предполагаем, что соответствие узлов недоступно. Таким образом, со ссылкой на Таблицу 1 мы тестируем методы столбца UNC в первой и второй строке соответственно для неориентированных и направленных сетей. В обоих случаях мы исключаем MI-GRAAL, который оказался слишком сложным в вычислительном отношении в большинстве описанных ниже экспериментальных условий. Мы также ограничиваем анализ «Глобальной статистики» коэффициентом кластеризации (только для неориентированных сетей), учитывая плохие характеристики диаметра в описанных выше тестах на возмущение.
е.е., произошла от той же модели. Другими словами, чтобы обеспечить хорошую производительность, метод должен иметь возможность назначать небольшое расстояние сетевым парам, исходящим из одной и той же модели, но большое расстояние парам, исходящим из разных моделей. Мы применяем типичный подход для тестирования производительности методов, работающих в неконтролируемой среде, т. Е. Моделируя контролируемые сценарии, в которых группы (или, как в этом случае, сетевые модели) известны, затем выполняем алгоритмы, как в случае неконтролируемого вмешательства, наконец, проверка их способности правильно определять группы, происходящие из разных моделей.Обратите внимание, что для этой задачи подходят только методы UNC, поскольку мы предполагаем, что соответствие узлов недоступно. Таким образом, со ссылкой на Таблицу 1 мы тестируем методы столбца UNC в первой и второй строке соответственно для неориентированных и направленных сетей. В обоих случаях мы исключаем MI-GRAAL, который оказался слишком сложным в вычислительном отношении в большинстве описанных ниже экспериментальных условий. Мы также ограничиваем анализ «Глобальной статистики» коэффициентом кластеризации (только для неориентированных сетей), учитывая плохие характеристики диаметра в описанных выше тестах на возмущение.
Мы снова выбираем сетевые модели ER, BA и LFR. Для каждой модели мы рассматриваем два размера (1000 и 2000 узлов), две плотности (0,01 и 0,05) и два семейства неориентированных / направленных (подробности о построении сети см. В файле дополнительной информации, раздел S3), и мы генерируем 5 сетей для каждой модели / набора параметров 3 × 2 × 2, всего 60 неориентированных и 60 направленных сетей. Затем мы вычисляем все попарные расстояния для каждого метода, в результате чего получаем две (т. Е. Ненаправленные / направленные) матрицы расстояний 60 × 60.
На рис. 5 и 6 мы визуализируем результаты с помощью дендрограмм (построенных с помощью ward.D2 linkage 57 и оптимального упорядочивания листьев 58 ), где для облегчения интерпретации мы помечаем каждый лист (= сеть) двумя цветами, одним обозначает модель сети, а другой размер / плотность. Это соответствует вышеупомянутой цели: поскольку мы можем управлять только механизмами создания сети, а не реализацией, полученной каждым из них, мы моделируем настройку как можно более контролируемой, имитируя контролируемый контекст, а затем оцениваем производительность различные методы, применяемые для построения кластеров, например, в неконтролируемой обстановке.Таким образом, контролируемый контекст используется только для установки объекта бенчмаркинга, а затем алгоритмы работают совершенно неконтролируемым образом. По этой причине, как подчеркивалось выше, разумно ожидать, что эффективный метод в идеале должен иметь возможность кластеризовать вместе все сети, происходящие из одного и того же модельного семейства, без помех из-за разных размеров и плотностей.
Рисунок 5Тесты кластеризации: дендрограммы для ненаправленного случая (дендрограммы EIG-LAP, EIG-SNL и PDIV аналогичны EIG-ADJ и представлены в файле дополнительной информации, рис.S6).
Рисунок 6Тесты кластеризации: дендрограммы для направленного случая. Слева: расстояние портретной дивергенции PDIV. Справа: дистанция DGCD-129.
В неориентированном случае (рис. 5) мы видим, что все методы могут более или менее точно группировать сети одного класса, но только если они имеют одинаковый размер / плотность. Это касается расстояния коэффициента кластеризации, EIG-ADJ (а также EIG-LAP, EIG-SNL и PDIV, не указанных на рисунке) и NetLSD.GCD-11 обеспечивает определенно лучшую производительность, поскольку он доказывает способность группировать все сети LFR вместе с графами BA с низкой плотностью, а также путем идентификации двух других чистых кластеров: один содержит графы ER с низкой плотностью, а другой BA и ER. графики с высокой плотностью. В целом результаты показывают достаточно сильную зависимость всех методов, кроме GCD-11, от размера и плотности графиков, что не совсем удовлетворительно.
В направленном случае (рис. 6) PDIV ведет себя лучше, чем в неориентированном случае, поскольку он может сгруппировать вместе все графы BA, в то время как графы ER и LFR сгруппированы вместе в другом большом кластере, внутри которого плотность становится Различающий фактор.С другой стороны, DGCD-129 может обеспечить идеальную группировку сетевых моделей.
Системный подход к сравнительной количественной оценке производительности различных методов — это структура Precision-Recall 19,20,24 : для заданного расстояния в сети определяется порог ε > 0 и две сети классифицируются как принадлежащие к модели того же класса, если расстояние между ними меньше ε . Учитывая, что правильные классы известны, точность классификации всех сетевых пар может быть определена количественно с помощью Precision and Recall.Затем процедура повторяется, изменяя ε , получая кривую Precision-Recall (рис. 7), которая в идеале должна иметь Precision равную 1 для любого значения Recall. В целом, кривые подчеркивают превосходство подходов, основанных на графлетах (GCD-11 и DGCD-129, соответственно), по сравнению со всеми другими методами, которые мы тестировали — их кривая превосходит все остальные почти во всем диапазоне кривых.
Рисунок 7Тесты кластеризации. Кривые Precision-Recall для методов, используемых для ненаправленных (слева) и направленных (справа) сетей.
Количественную оценку эффективности каждого метода можно получить с помощью области под кривой точного отзыва (AUPR), которая в идеальном случае должна быть равна 1. Для левой панели рис. 7 AUPR находится в диапазоне от 0,386 (NetLSD) до 0,688 (GCD-11), для правой панели AUPR составляет 0,685 для PDIV и 0,928 для DGCD-129. Отметим, что все методы работают лучше, чем случайный классификатор (AUPR равен 0,322), но улучшение очень умеренное для спектральных методов и NetLSD. Показатели расстояния коэффициента кластеризации (ненаправленные сети) на удивление хороши, с AUPR, равным 0.620. По крайней мере, в нашей тестовой среде эта простая статистика кажется жизнеспособной недорогой альтернативой более сложным расстояниям.
Кроме того, показатель AUPR может использоваться для подтверждения того, что, если рассматриваются только сети одного размера / плотности, все проанализированные методы дают по существу правильную классификацию — особенность, уже отмеченная выше при обсуждении дендрограмм. Действительно, мы сообщаем, что в этом случае почти все методы, показанные на рис. 7, получают AUPR больше 0.8 в неориентированном случае и практически равно 1 в направленном случае (см. Файл дополнительной информации, таблицы S3 и S4).
Тесты в реальных сетях
В этом разделе мы оцениваем эффективность вышеупомянутых методов при группировании наборов реальных сетей: наша цель — более глубоко понять, как эти методы работают и каких результатов следует ожидать от их использование. Мы анализируем мультиплексные сети, поскольку их уровни можно рассматривать как отдельные (обычные) сети, определенные на одном и том же наборе узлов.Это желаемое свойство для нашего анализа, поскольку оно позволяет использовать как методы KNC, так и UNC. Таким образом, можно установить, дают ли два класса методов разное понимание одной и той же проблемы.
Европейская сеть авиаперевозок
Эта сеть имеет 448 узлов, представляющих европейские аэропорты, и 37 уровней, соответствующих авиакомпаниям (список см. В файле дополнительной информации, таблица S5), всего 3588 ненаправленных и невзвешенных ребер 59 .Мы тестируем все расстояния первой строки таблицы 1, а именно три расстояния KNC (напомним, что MAN и CAN эквивалентны EUC в этой настройке) и восемь расстояний UNC (с коэффициентом кластеризации как «Глобальная статистика»).
На рис. 8 показаны одиннадцать матриц расстояний 37 × 37 (симметричные) (соответствующие дендрограммы находятся в файле дополнительной информации, рис. S7). Во-первых, мы заметим, что два класса расстояний дают качественно разные результаты: расстояния KNC почти одинаковы по всей матрице (прежде всего JAC), в то время как методы UNC получают разные степени дифференциации, особенно для EIG-SNL и GCD-11.EUC и DCON, по сути, идентифицируют один (тривиальный) кластер, включающий все сети, кроме Ryanair (№2). Это неудивительно, поскольку слой Ryanair отличается от других тем, что имеет наибольшее количество ребер и (неизолированных) узлов. В свою очередь, это демонстрирует, что на расстояния KNC сильно влияют размер и плотность: два графа с разными размерами или плотностями классифицируются как далекие только из-за подсчета ребер, независимо от их топологических свойств.
Рисунок 8Европейская сеть воздушного транспорта: матрицы расстояний для трех расстояний KNC (первая строка) и восьми расстояний UNC (вторая — последняя строка).Цвет в записи ( i , j ) — это расстояние между слоями i и j мультиплексной авиатранспортной сети. Расстояния кодируются цветами от синего (большое расстояние) до красного (маленькое расстояние).
Три спектральных расстояния имеют аналогичное поведение. Дендрограммы идентифицируют два основных кластера: маленький, содержащий авиакомпании №1, №2, №3 и, в соответствии с методом, №5, №6 или №26, и большой, содержащий все остальные (на самом деле EIG-SNL показывает третий, небольшой кластер, который, однако, не имеет четкой интерпретации).Небольшой кластер объединяет авиалинии с наибольшим количеством узлов и соединений (> 75 узлов,> 110 ребер). Это подтверждает сильную зависимость трех спектральных расстояний от размера и плотности, как было выявлено в синтетических тестах.
Чтобы избежать неоднозначности в интерпретации тепловых карт на рис. 8, отметим, что наличие группы авиакомпаний со сравнительно меньшим внутренним расстоянием (т. Е. Диагональный блок более горячего цвета) не означает наличие четко определенного группы, если сама группа не отображает сравнительно большее расстояние (более холодный цвет) до остальных авиакомпаний.Вот почему, например, в случае EUC авиакомпании № 34, № 19, № 12 и т. Д. Не образуют хорошо разделенную группу, а также диагональные блоки более горячего цвета в случае EIG-ADJ не имеют значения, поскольку нет четкого цветового разделения (то есть холодного цвета за пределами квартала), но существует континуум расстояний между авиакомпаниями.
Шаблоны коэффициента кластеризации и матриц расстояний NetLSD качественно аналогичны шаблонам спектральных расстояний. Матрица NetLSD не дает четкой интерпретации.Матрица коэффициентов кластеризации, напротив, легко читается благодаря прямому определению конкретного сетевого расстояния: авиакомпания № 35 (Wideore) имеет самый большой коэффициент кластеризации. Кроме того, тепловая карта выявляет две слабо разделенные группы, которые действительно соответствуют группам авиакомпаний с соответственно большим (> 0,1) и меньшим коэффициентом кластеризации.
Расстояния MI-GRAAL и PDIV не показывают какой-либо значимой группировки сетей, за исключением того, что первая группирует вместе три сети чистой звезды (# 9, # 31, # 33), но пропускает четвертую, существующую в базе данных (# 18 ), а последняя группирует несколько сетей, имеющих одинаковую максимальную степень (# 17, # 19, # 23, и # 13, # 20, # 31, # 34), но на самом деле пропускает несколько других.Наконец, матрица расстояний и дендрограмма для GCD-11 показывают три основных кластера. Один из них содержит все четыре слоя чистых звезд в наборе данных (№ 9, № 18, № 31, № 33), а второй группирует семь из восьми авиакомпаний со сравнительно большим (> 0,15) коэффициентом кластеризации (№ 2, № 3, № 6, № 15, № 16, № 21, № 26, № 35). Третий кластер содержит все остальные слои. Кроме того, авиалинии №4 и №28 также объединены в пары, чтобы сформировать небольшой, но хорошо идентифицированный кластер: оказывается, что обе они имеют нулевой коэффициент кластеризации, не будучи звездным графом.В целом, эти результаты означают, что GCD-11 достаточно эффективен для классификации сетей на основе чисто топологических характеристик.
Выше мы указали, что расстояния KNC не могут выделить значимые кластеры сетей. Тем не менее, они дают полезный результат, поскольку объединяют сети в пары на региональной основе, то есть размещают на сравнительно небольших расстояниях авиакомпании, базирующиеся в одной стране / регионе. Например, дендрограмма EUC соединяет № 1 с № 6 (Германия), № 8 с № 13 (Скандинавия), № 30 с № 37 (Греция) и № 9 с № 27 (Нидерланды).JAC объединяет вышеупомянутые авиакомпании и, кроме того, № 3 с № 4 (Великобритания), № 12 с № 22 (Испания), № 2 с № 23 (Ирландия) и № 16 с № 33 (Венгрия). DCON (см. Рис. 9) группы № 8 с № 13 (Скандинавия), № 12, № 21, № 22 (Испания), № 30 с № 37 (Греция), № 1 с № 6 (Германия) и № 24. с № 29 (снова Германия). Такая группировка не восстанавливается с помощью расстояний UNC (см., Например, DCON и GCD-11 на рис. 9). На самом деле все расстояния KNC основаны на некотором сходстве узлов. Авиакомпании, базирующиеся в одной стране, используют одни и те же национальные аэропорты; кроме того, во многих случаях две авиакомпании, объединенные методами KNC, являются ведущей национальной компанией и компанией с низкими издержками, предлагая разные поездки и ценовые условия на одних и тех же маршрутах.Следовательно, узлы двух авиакомпаний, базирующихся в одной стране, обычно похожи, и это уменьшает расстояние между соответствующими сетями.
Рис. 9Европейская сеть воздушного транспорта: дендрограммы для DCON и GCD-11 с авиакомпаниями, окрашенными в соответствии со странами, в которых они базируются. В отличие от расстояний UNC (например, GCD-11), расстояния KNC (например, DCON) представлены во многих случаях может объединять авиакомпании, базирующиеся в одной стране.
Торговая сеть ФАО
Теперь рассмотрим Торговую сеть ФАО по продуктам питания, сельскохозяйственной продукции и животноводству 60 .Он состоит из 364 уровней, каждый из которых представляет отдельный продукт, с общими узлами 214, соответствующими странам, для общего количества 318346 соединений. Если несушки / продукты соответствуют классификации 61 Гармонизированной системы ВТО, мы обнаруживаем, что продукты ФАО относятся к семи из пятнадцати основных категорий ГС: Животные и продукты животного происхождения ; Растительные продукты ; Продукты питания ; Chemicals ; Пластмассы и каучуки ; Необработанные шкуры, кожа и кожа ; Текстиль .Каждый слой ориентирован и взвешен, веса представляют стоимость экспорта (в тысячах долларов США) продукта из одной страны в другую. Здесь мы обсуждаем несколько результатов, полученных на бинаризованной версии сети, которая получается для каждого продукта p путем сохранения только ссылок, исходящих из стран c с выявленным сравнительным преимуществом RCA cp > 1, т. Е. Страны, которые являются крупными экспортерами этого продукта (см. 62,63 . и файл дополнительной информации, ур. (S1), подробнее). Мы тестируем расстояния второй строки таблицы 1, а именно три расстояния KNC (поскольку MAN и CAN эквивалентны EUC) и два расстояния UNC (как обычно, мы исключаем MI-GRAAL из-за высокой вычислительной стоимости, и мы не учитываем коэффициент кластеризации, поскольку мы анализировали его как «Глобальную статистику» только для неориентированных сетей).
Кластерный анализ, обобщенный дендрограммами на рис. 10, ясно показывает, что наивное ожидание того, что продукты будут организованы в группы в соответствии с их категорией, не выполняется: категории ГС оказываются слишком широкими и диверсифицированными, чтобы создавать аналогичные торговые топологии. Овощные продукты , например, является наиболее представленной категорией: она включает в себя такое разнообразие продуктов, что соответствующие сети также чрезвычайно разнообразны не только с точки зрения количества и местоположения стран-производителей / потребителей, но и с точки зрения возможного существования. промежуточных стран, куда товары импортируются, трансформируются и, в конечном итоге, реэкспортируются.
Рис. 10Торговая сеть ФАО: кластерный анализ тестируемых методов. В верхней цветной полосе продукты классифицируются в соответствии с Гармонизированной системой ВТО.В нижней панели отображаются несколько конкретных категорий.
Тем не менее, кластерный анализ может выявить интересные сходства. Например, некоторые сельскохозяйственные продукты (например, тропические фрукты или цитрусовые) могут производиться только в определенных регионах мира и, следовательно, только в нескольких странах. Таким образом, мы ожидаем, что расстояние между соответствующими слоями будет небольшим — это, очевидно, верно, если используются расстояния KNC. Это ожидание действительно подтверждается. Все расстояния KNC группируются вместе (см. Нижние цветные полосы на рис.10) все цитрусовые (а именно апельсинов ; лимонов и лаймов ; грейпфрутов ; мандаринов, мандаринов, клементинов, сатсумы ), присутствующих в наборе данных, и EUC также помещает консервированных оливок и масел, оливок. , Дева рядом с ними. Это неудивительно, поскольку последние в основном выращивают в тех же регионах, что и цитрусовые, по климатическим причинам. Большая часть тропических фруктов также собирается вместе: EUC в основном находит две группы: одна содержит какао, бобы ; Какао, порошок и жмых ; Какао, паста ; Какао, масло ; Bananas ; Ананасы ; Манго, мангустины, гуавы ; и другой, который содержит Ваниль ; Кокосы ; Кокосы сушеные ; Корица ; Мускатный орех ; Перец ; Кофе, зеленый .Аналогичным образом DCON также выделяет две основные группы тропических фруктов. Кроме того, другая группа конкретных продуктов, а именно продукты, относящиеся к сокам, сгруппированы по расстояниям KNC. Примечательно, что группы цитрусовых и цитрусовых соков не соседствуют друг с другом, что свидетельствует о том, что производство и переработка свежих фруктов в основном осуществляется в разных странах, что приводит к разным торговым сетям.
Наконец, расстояния UNC, примененные к набору данных ФАО, определяют те немногие продукты с очень своеобразной структурой торговли.Например, крайние левые листья дендрограммы DGCD-129 (рис. 10), находящиеся на большом расстоянии от всех остальных листьев, соответствуют торговым сетям с ярко выраженной звездчатой структурой. Они относятся к очень своеобразным продуктам, таким как Bulgur ; Кленовый сахар и сиропы ; Маргарин жидкий ; Ульи ; Camels ; и другие. Некоторые из них производятся и экспортируются только одной страной (например, Кленовый сахар и сироп ) или в значительной степени импортируются очень немногими странами (например, Кленовый сахар и сироп ).g., Beehives ), и поэтому их торговые схемы сильно централизованы.
A.6 — Теория графов: меры и индексы
Авторы: д-р Сезар Дюкрю и д-р Жан-Поль Родриг
Теория графов основывается на нескольких показателях и показателях, оценивающих эффективность транспортных сетей.
Транспортные сети состоят из множества узлов , и каналов , , и по мере их усложнения их сравнение становится затруднительным.Например, на первый взгляд может быть неочевидно оценить, какая из двух транспортных сетей является наиболее доступной или наиболее эффективной. Для анализа эффективности сети можно использовать несколько показателей и индексов, многие из которых были первоначально разработаны Кански в 1960-х годах:
- Выражение взаимосвязи между значениями и сетевыми структурами, которые они представляют.
- Сравнение различных транспортных сетей в определенный момент времени.
- Сравнение развития транспортной сети в разные моменты времени.
Помимо описания размера сети по количеству узлов и ребер , ее общей длины и трафика, для определения структурных атрибутов графа используются несколько показателей; диаметр, количество циклов и порядок узла.
Диаметр ( d ). Длина кратчайшего пути между наиболее удаленными узлами графа. Он измеряет размер графа и топологическую длину между двумя узлами.
Диаметр позволяет нам измерить развитие сети во времени. Большой диаметр подразумевает менее связанную сеть. В случае сложного графа диаметр может быть найден с помощью матрицы топологических расстояний (расстояние Шимбеля), которая вычисляет для каждой пары узлов минимальное топологическое расстояние. Графики, протяженность которых остается постоянной, но с большей связностью, имеют меньшие значения диаметра. Плоские сети часто имеют большой диаметр из-за наличия множества промежуточных остановок между двумя удаленными узлами.
Количество циклов ( и ) . Максимальное количество независимых циклов в графе. Это число ( u ) оценивается через количество узлов ( v ), ссылок ( e ) и подграфов ( p ) . Деревья и простые сети имеют значение 0, поскольку у них нет циклов. Чем сложнее сеть, тем выше значение u, поэтому его можно использовать как индикатор уровня развития и сложности транспортной системы.
2. Индексы на сетевом уровне
Индексы — это более сложные методы представления структурных свойств графа, поскольку они включают сравнение одной меры с другой. Некоторые индексы учитывают пространственные характеристики (расстояние, поверхность), а также уровень активности (трафик), в то время как другие основываются исключительно на топологическом измерении сети.
Стоимость . Представляет общую длину сети, измеренную в реальных транспортных расстояниях, где aij — это наличие (1) или отсутствие (0) связи между i и j и lij — длина ссылки.Этот показатель также можно рассчитать на основе двух других измерений сети; минимальное связующее дерево (MST) и жадная триангуляция (GT). MST представляет самое короткое и / или самое дешевое поддерево сети; его можно получить, применяя алгоритм кратчайшего пути, алгоритм Крускала, который позволяет найти маршрут с наименьшей стоимостью, соединяющий все узлы в сети. GT относится к максимальному связанному планарному графу, сохраняющему то же количество узлов, что и в исходной сети, но добавляющим все возможные связи без нарушения его планарности.Такие операции учитывают как топологию, так и географию сети, сравнивая последнюю с ее оптимальными конфигурациями. Более эффективные сети имеют относительную стоимость, близкую к 1, в то время как менее эффективные сети ближе к 0.
Указатель объезда . Мера эффективности транспортной сети с точки зрения того, насколько хорошо она преодолевает расстояние или трение расстояния. Чем ближе индекс обхода приближается к 1, тем более эффективна сеть в пространственном отношении.Сети, имеющие индекс обхода 1, редко, если вообще когда-либо, встречаются, и большинство сетей будут соответствовать асимптотической кривой, приближающейся к 1, но никогда не достигающей ее. Например, расстояние по прямой D ( S) между двумя узлами может составлять 40 км, но расстояние транспортировки , D (T) ; реальное расстояние составляет 50 км. Таким образом, индекс объезда составляет 0,8 (40/50). Сложность топографии часто является хорошим показателем уровня объезда.
Чтобы получить показатель относительной эффективности, Относительная эффективность индекса обхода — это отношение между индексом обхода, рассчитанным из исходной сети, и индексом обхода, рассчитанным либо из MST (минимальное остовное дерево), либо из GT (жадная триангуляция). .
Плотность сети . Измеряет территориальную занятость транспортной сети в километрах линий ( L ) на квадратный километр поверхности ( S ). Чем он выше, тем больше развита сеть.
Индекс Пи. Соотношение между общей длиной графа L (G) и расстоянием по его диаметру D (d). Он обозначен как Пи из-за его сходства с реальным значением Пи, которое выражает соотношение между длиной окружности и диаметром круга.Высокий показатель показывает развитую сеть. Это мера расстояния на единицы диаметра и индикатор формы сети .
Eta Index. Средняя длина ссылки. Добавление новых узлов приведет к уменьшению Eta, поскольку средняя длина на ссылку уменьшается. Сложные сети, как правило, имеют низкое значение eta.
Тета-индекс. Измеряет функцию узла, которая представляет собой средний объем трафика на перекресток.Чем выше тета, тем больше нагрузка на сеть. Мера также может применяться к количеству звеньев (ребер), где он представляет собой среднюю нагрузку на звено.
Бета Индекс. Измеряет уровень связности в графе и выражается соотношением между количеством ссылок (e) и количеством узлов (v). У деревьев и простых сетей бета-значение меньше единицы. Связанная сеть с одним циклом имеет значение 1. Более сложные сети имеют значение больше 1.В сети с фиксированным количеством узлов, чем больше количество ссылок, тем больше количество возможных путей в сети. Сложные сети имеют высокое значение бета-версии. Коэффициент богатого клуба — это бета-индекс, применяемый к отношениям между узлами более крупного порядка (степени); он проверяет, выше ли связь между узлами с большей степенью, чем для всей сети.
Для плоских графов Для неплоских графовАльфа-индекс. Мера связности, которая оценивает количество циклов на графике по сравнению с максимальным количеством циклов.Чем выше альфа-индекс, тем больше количество подключений к сети. Деревья и простые сети будут иметь значение 0. Значение 1 указывает на полностью подключенную сеть. Измеряет уровень подключения независимо от количества узлов. Очень редко сеть будет иметь альфа-значение 1, потому что это будет означать очень серьезное дублирование. В литературе по планарным сетям этот индекс также называется коэффициентом сетки .
Для плоских графов Для неплоских графовГамма-индекс. Мера возможности подключения, которая учитывает взаимосвязь между количеством наблюдаемых ссылок и количеством возможных ссылок. Значение гаммы находится в диапазоне от 0 до 1, где значение 1 указывает на полностью подключенную сеть и было бы крайне маловероятным. Гамма — это эффективное значение для измерения развития сети во времени.
Основываясь исключительно на количестве узлов и связей, индексы Alpha, Beta и Gamma остаются ограниченными для выявления структурных различий между сетями одинакового размера.Таким образом, физики предложили более надежные меры, которые учитывают внутреннюю сложность графа.
Иерархия (h) . Показатель наклона степенной линии, проведенной на двухлогарифмическом графике зависимости частоты узлов от распределения степеней. Сети, характеризующиеся сильными иерархическими конфигурациями, такими как сети без масштабирования (несколько узлов с высокой степенью и много узлов с низкой степенью), часто имеют значения более 1 или 2. Значение ниже 1 указывает на отсутствие безмасштабных свойств и ограниченную иерархию среди узлов.
Транзитивность (t) . Также называемый коэффициентом кластеризации, это общая вероятность того, что соседние узлы сети будут соединены между собой, что свидетельствует о существовании тесно связанных сообществ (или кластеров, подгрупп, клик). Он рассчитывается как отношение наблюдаемого количества закрытых троек к максимально возможному количеству закрытых троек на графике. Другой способ вычисления транзитивности — это вычисление среднего коэффициента кластеризации всех узлов.Сложные сети и особенно сети с малым миром часто имеют высокую транзитивность и малый диаметр. Поскольку тройки — не единственный способ взглянуть на плотность соседства между узлами, эту меру можно расширить до циклов длиной 4 и 5.
Средняя длина кратчайшего пути . Показатель эффективности, который представляет собой среднее количество остановок, необходимых для достижения двух удаленных узлов на графике. Чем ниже результат, тем эффективнее сеть обеспечивает простоту обращения.Для сравнения, диаметр — это максимальная длина всех возможных кратчайших путей.
Ассортативный коэффициент (r) . Этот коэффициент представляет собой корреляцию Пирсона между порядком (степенью) узлов на обоих концах каждого звена (ребра) в сети. Результат варьируется от -1 (узлы с низкой степенью часто соединяют узлы с высокой степенью) до 1 (часто связаны узлы с одинаковой или одинаковой степенью). Дизассортативные сети (r значительно отрицательно) часто представляют собой сети с сильной иерархической конфигурацией с большими узлами, соединяющими меньшие узлы, как в безмасштабных сетях, тогда как обычные сети часто ассортативны.
Существует множество мер для выявления положения узла в сети. Некоторые из них создаются на «локальном уровне» на основе связей с соседними узлами, в то время как другие на «глобальном уровне» учитывают положение узла во всей сети.
Порядок (степень) узла ( o ). Количество прикрепленных к нему ссылок и является простой, но эффективной мерой узловой важности. Чем выше его значение, тем важнее узел в графе, поскольку к нему сходится множество ссылок.Узлы-концентраторы имеют высокий порядок, в то время как конечные точки имеют порядок, который может быть даже ниже 1. Порядок идеального концентратора будет равен сумме всех порядков других узлов в графе, а идеальная спица будет иметь порядка 1. Процент узлов, напрямую связанных во всем графе, таким образом, является мерой достижимости. Изолятор — это узел без связей (степень равна 0). Разница между входящей и исходящей степенью в ориентированном графе (орграфе) может подчеркивать интересные функции некоторых узлов как аттракторов или отправителей.Порядок может быть вычислен на разной глубине: смежные узлы (глубина 1), смежные узлы соседних узлов (глубина 2) и т. Д. Взвешенная степень — это просто сумма значений, связанных со ссылками.
- Порядок в графике
Число Кенига (или связанное с ним число, эксцентриситет). Мера удаленности, основанная на количестве ссылок, необходимых для достижения самого дальнего узла в графе.
Индекс Шимбеля (или расстояние Шимбеля, узловая доступность, узловая точка).Мера доступности, представляющая сумму длин всех кратчайших путей, соединяющих все остальные узлы в графе. Обратная мера также называется центральностью по близости или центральностью по расстоянию.
Центральность посредничества (или кратчайший путь промежуточности). Мера доступности, которая представляет собой количество раз, когда узел пересекается кратчайшими путями в графе. Аномальная центральность обнаруживается, когда узел имеет высокую промежуточную центральность и низкий порядок (степень центральности), как в воздушном транспорте.
Зависимость от концентратора (hd) . Мера уязвимости узла, которая представляет собой долю канала с наибольшим трафиком в общем трафике (взвешенная степень). Слабые узлы, зависящие от нескольких ссылок, будут иметь высокую зависимость от концентратора, особенно если они расположены по соседству с большим узлом, в то время как концентраторы будут иметь более равномерное распределение трафика между своими соединениями. Он указывает, в какой степени удаление самого крупного канала трафика повлияет на общую активность узла.Мера может быть расширена на большее количество звеньев (2, 3… 10 самых крупных звеньев потока).
Средняя степень ближайшего соседа (knn) . Мера соседства, указывающая тип среды, в которой находится узел. Узел с низким порядком (степенью) может быть окружен множеством других узлов, малых или больших, что имеет прямое влияние на его собственную центральность и потенциал роста. Сеть является ассортативной или дезассортативной в зависимости от схожести порядка (степени) между соседними узлами, что можно проверить с помощью корреляции Пирсона (коэффициент ассортативности).Связность между соседями — это корреляция между порядком (степенью) узлов и средним порядком (степенью) их соседей.
Индекс когезии (ci) . Для заданного ребра ij (ссылки) этот индекс измеряет соотношение между количеством общих соседей, подключенных к узлам i и j, и общим количеством их соседей. Ссылки с наивысшими значениями обычно соединяют плотные сообщества (или кластеры) на графике и могут быть удалены, чтобы разделить график пополам и выявить такие подгруппы.Умножение этого индекса на вес (например, трафик) ссылок позволяет связать топологию и потоки. Этот индекс сплоченности также называется индексом прочности, и он соответствует наблюдаемому количеству циклов длиной 3 и 4, к которым принадлежит кромка, деленному на максимальное количество таких циклов.
Степень внутри модуля (Zi; или z-оценка) . Показывает, насколько хорошо узел связан с другими узлами в том же модуле (или кластере, сообществе), где Ki — это порядок (степень) узла i в кластере si, Ksi — средний порядок (степень) всех узлов в кластер si, а δKsi — стандартное отклонение K в si.Поскольку два узла с одинаковым z-значением могут играть разные роли в кластере, этот показатель часто сравнивают с коэффициентом участия (Pi). Обе меры применяются к узлам после того, как известны кластеры в сети.
Коэффициент участия (Pi) . Сравнивает количество связей (порядок, степень) узла i с узлами во всех кластерах с количеством связей в собственном кластере. Zi и Pi показывают, действительно ли узлы являются концентраторами в сети, в то время как другие привязаны к локальным ссылкам и, следовательно, не действуют как соединители между кластерами.
Было высказано несколько критических замечаний по поводу таких индексов, поскольку они не всегда учитывают реальную длину, качество и вес ссылок; сети равного размера могут иметь противоположные топологические формы. Однако они остаются полезными для описания изменяющейся структуры данной сети.
Связанные темы
Библиография
- Arlinghaus, S.L., W.C. Арлингхаус и Ф. Харари (2001) Теория графов и география: интерактивное представление.Нью-Йорк: Джон Вили и сыновья.
- Jiang B. и C. Claramunt (2004) «Топологический анализ городских уличных сетей», Environment and Planning B, Vol. 31, с. 151-162.
- Кански К. (1963) Структура транспортных сетей: взаимосвязь между географией сети и региональными характеристиками, Чикагский университет, географический факультет, исследовательские документы 84.
- Уотерс, Нью-Мексико (2006) Сетевые и узловые индексы: меры сложности и избыточность: обзор. В А. Реджиани и П.Nijkamp (eds) Пространственная динамика, сети и моделирование, Челтенхэм, Великобритания и Нортгемптон, Массачусетс, США: Эдвард Элгар.
- Уоттс, Д.Дж., Строгац, С.Х. (1998) «Коллективная динамика сетей« маленького мира »», Nature 393 (6684): 440–442.
Комплексные сети — Области исследований — AFOSR
Описание программы
Сложные сети широко используются в военных, коммерческих и гражданских операциях. Сложные сети состоят из графа (направленного или неориентированного) вместе с набором атрибутов.Эти атрибуты могут включать в себя скалярные или многомерные веса на ребрах или узлах графа, топологические характеристики графа и процессы, которые определяют динамику графа. Сложные сети охватывают многие научные дисциплины (например, математику, информатику, инженерию, социально-экономику, биологию и т. Д.) И многие прикладные области (например, логистику, зондирование, информационные системы). Сети фундаментально описывают структурные аспекты взаимодействия между отдельными агентами.Сети могут быть очень большими и иметь несколько масштабов характеристик. Они могут быть статичными или динамическими. Они могут быть физическими или виртуальными. Сети могут состоять из нескольких разнородных подсетей (то есть сети сетей) с явными и неявными взаимозависимостями. Например, логистические сети тесно связаны с компьютерными и электрическими сетями. Таким образом, отказ критического узла или дуги в одной сети может вызвать сбои в другой, что может создать каскадное событие с катастрофическими последствиями.Все эти характеристики сетей могут затруднить анализ, понимание и использование сетей и сделать их недоступными для вычислений.
Эта программа фундаментальных исследований направлена на разработку фундаментальных математических и алгоритмических методов для изучения, понимания, анализа и проектирования сложных сетей и динамических процессов, связанных с их характеристиками. Программа ищет инновационные подходы с далеко идущим потенциалом, а это означает, что в идеале подходы должны быть применимы к широким классам проблем и не должны быть привязаны к конкретной области приложения.Представляющие интерес сети могут иметь произвольную топологию, могут быть статическими или динамическими и могут подвергаться неопределенным условиям, начиная от стохастической среды до преднамеренных враждебных действий, затрагивающих как узлы, так и ссылки.
Мы настоятельно рекомендуем вам связаться с нашим сотрудником по программе до разработки полного предложения, чтобы обсудить соответствие ваших идей целям нашей программы, предлагаемым вами методам и масштабам предлагаемых вами усилий.
Ходатайство
BAA
Общий доступ к файлам для сложных сетей Обзор программы
При загрузке файлов используйте соглашение об именах файлов «Имя-Университет-Тема.

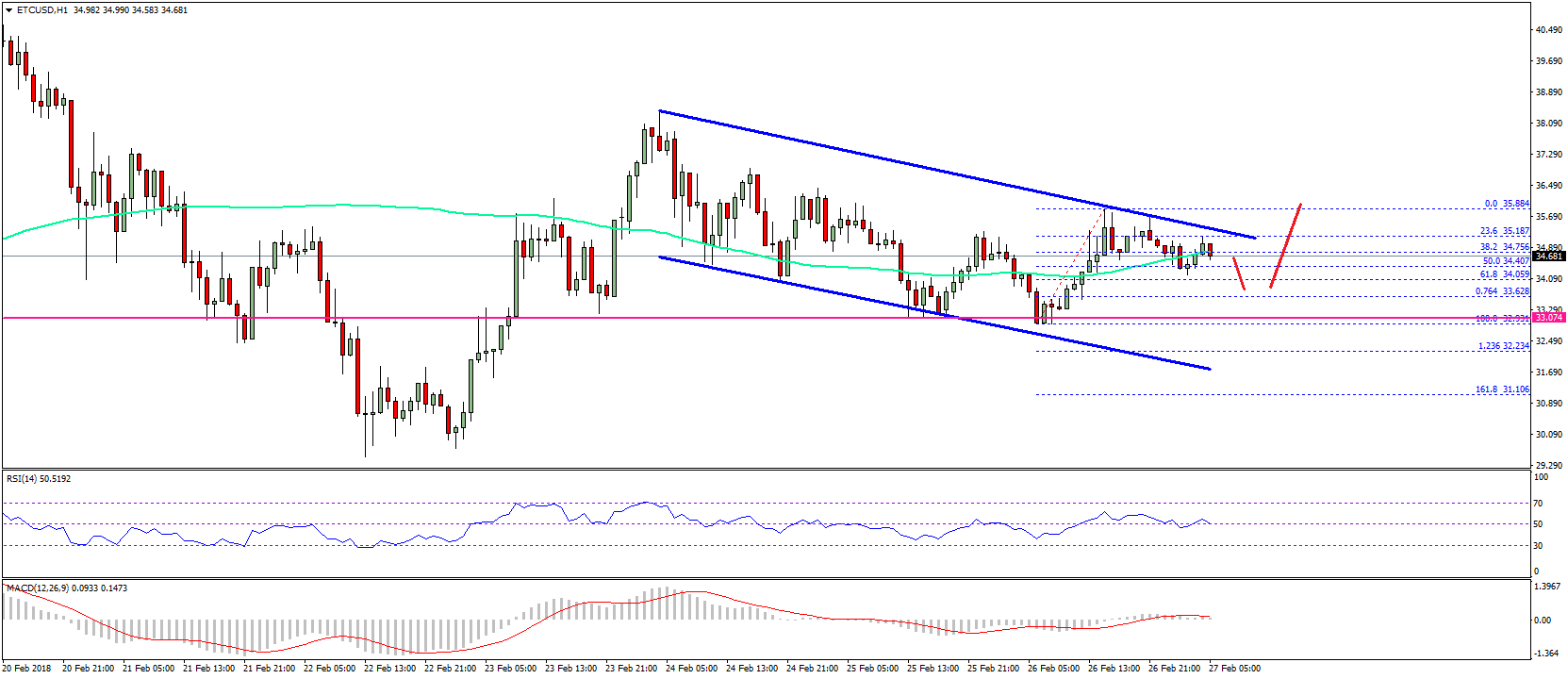 , Кембридж, штат Массачусетс.
, Кембридж, штат Массачусетс. (1983) Теоретико-информационные показатели для характеристики химических структур.Research Studies Press, Чичестер.
(1983) Теоретико-информационные показатели для характеристики химических структур.Research Studies Press, Чичестер.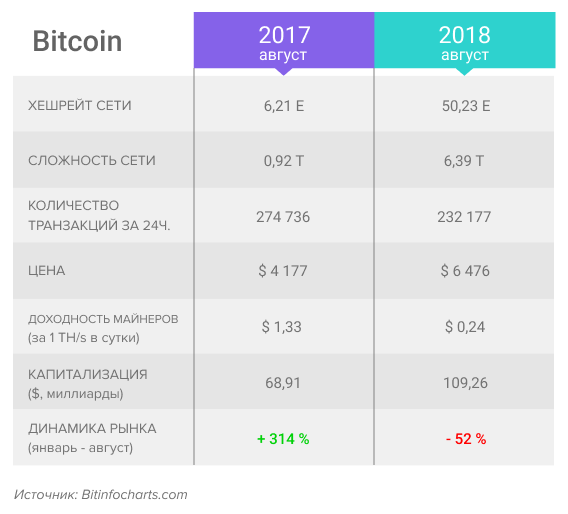

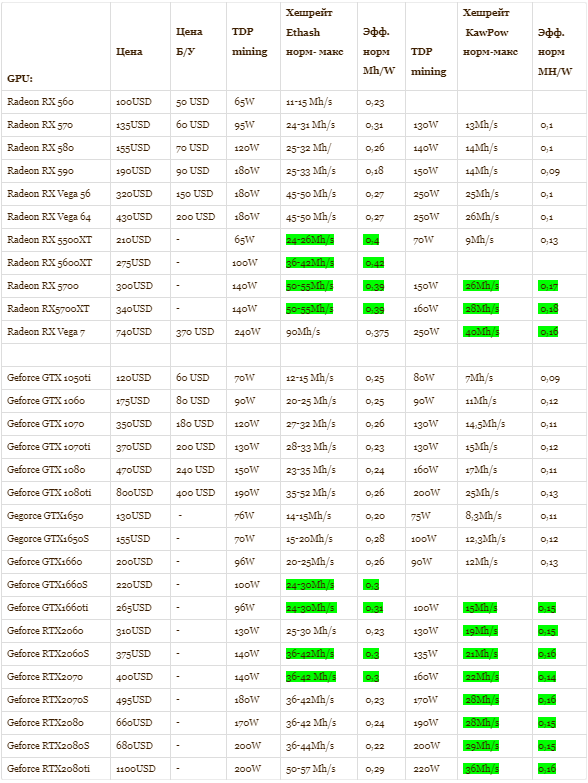 J Math Chem 8: 383–397.
J Math Chem 8: 383–397.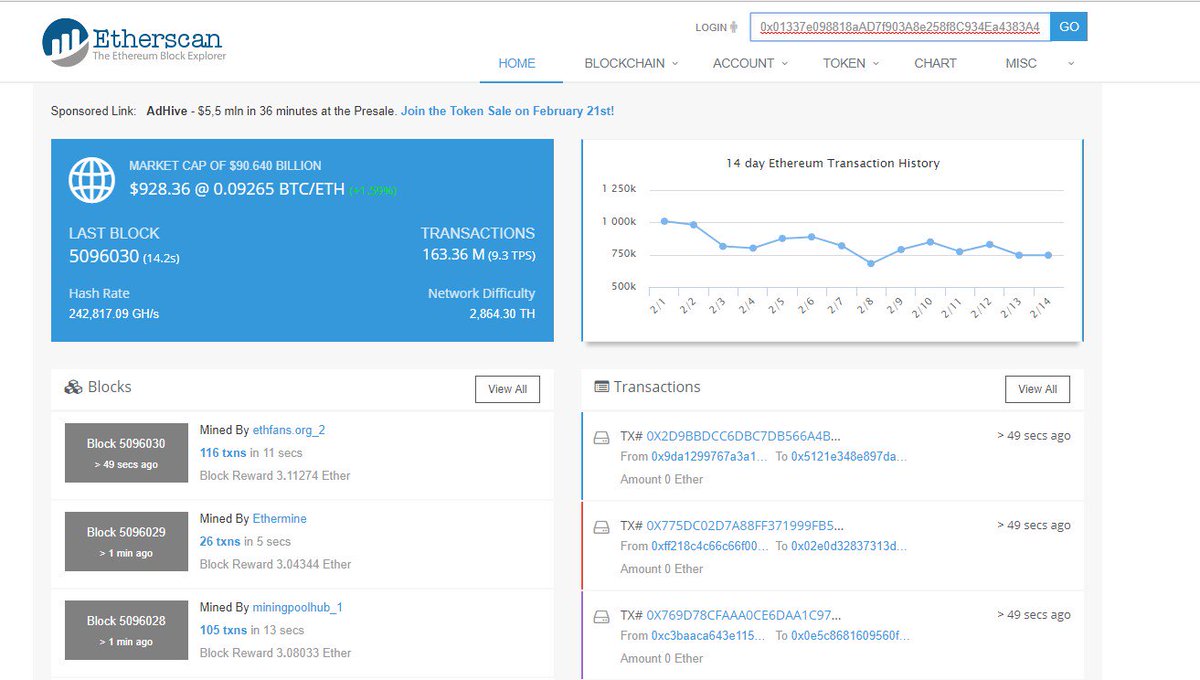 , Шен-Орр С., Ицковиц С., Каштан Н., Чкловский Д. и др. (2002) Сетевые мотивы: простые строительные блоки сложных сетей. Наука 298: 824–7.
, Шен-Орр С., Ицковиц С., Каштан Н., Чкловский Д. и др. (2002) Сетевые мотивы: простые строительные блоки сложных сетей. Наука 298: 824–7. PLoS Computational Biology 7: e1002053.
PLoS Computational Biology 7: e1002053.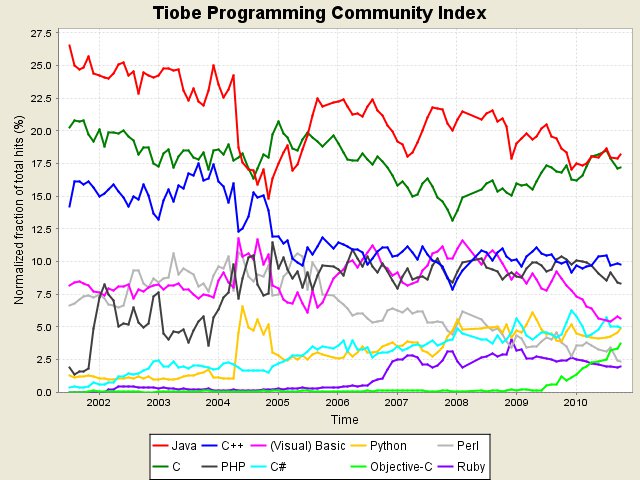 Мы также протестировали реализацию для направленных сетей.
Мы также протестировали реализацию для направленных сетей.