Задачка на основы криптографии с подробным разбором
Как удостовериться, что у друга есть ваш номер телефона так, чтобы никто об этом не узнал, причём нельзя спросить его напрямую?
Поясним условия подробнее. Например, вы хотите удостовериться, что у Пети есть номер вашего телефона. Но вы не можете спросить его об этом прямо. Вам придется написать ему сообщение на карточке и отдать карточку Кате, которая будет выступать в качестве посредника. Катя отнесет карточку Пете, он напишет свое сообщение и отдаст его Кате, которая передаст его вам. Вы не хотите, чтобы Катя узнала ваш номер телефона. Как в таких обстоятельствах следует сформулировать свой вопрос Пете?
Даже если вы дадите короткий и простой ответ, вас могут попросить представить и ответ на основе RSA. Он не такой сложный, если у Пети есть компьютер, и если он сможет следовать вашим рекомендациям. Спросите интервьюера, насколько Петя продвинут в математике и компьютерах.
При использовании RSA генерируется два ключа: общественный и частный. Общественный ключ похож на адрес электронной почты. Он позволяет любому человеку отправить вам сообщение. Частный ключ — это что-то вроде вашего пароля к электронной почте. Вам он необходим, чтобы получить ваши е-мейлы, и вы должны держать его в секрете, так как в противном случае сообщение, адресованное вам, сможет прочитать любой желающий.
Вы не сможете послать Пете секретное сообщение, поскольку он не создал свои ключи. Он, может быть, даже не знает, что такое RSA, и не будет о нем ничего знать до тех пор, пока вы ему не расскажете! Но для этого вам и не нужно отправлять ему секретное сообщение. Вы хотите, чтобы Петя отправил такое сообщение вам, а именно — ваш номер телефона. Это означает, что нам нужны ключи для себя, а не для Пети. Вот общая схема решения.
«Привет, Петя! Мы собираемся воспользоваться криптографией RSA. Может быть, ты не знаешь, что это такое, но я объясню тебе, что надо сделать. Вот мой общественный ключ… Возьми его и мой номер телефона и придумай зашифрованный номер, следуя инструкциям.
Пришли этот зашифрованный номер обратно мне через Катю».
Трюк в том, чтобы составить инструкцию так, чтобы ею мог воспользоваться практически каждый. К тому же вам нужно обеспечить и необходимую точность.
Криптография RSA впервые была описана, как теперь считается, в 1973 году. Её первым создателем был британский математик Клиффорд Кок, который тогда работал на секретной службе Её Величества. В те годы его схема считалась непрактичной: для нее обязательно нужен был компьютер. В те времена, когда шпионы обычно обходились фотоаппаратами, спрятанными в запонки, эту трудность было не так легко преодолеть. До 1997 года идея Кока считалась секретной. Однако в 1978 году трое ученых из MIT, Рональд Ривест, Ади Шамир и Леонард Адлеман, предложили ее независимо от Кока. Первые буквы их фамилий (RSA) стали акронимом и названием этого алгоритма.
В системе RSA человек, который хочет получать сообщения, должен выбрать два случайных простых числа p и q. Числа должны быть большими и, по крайней мере, такими же крупными (по числу цифр), как и числа или сообщения, которые надо передать. Для телефонного номера из десяти цифр р и q также должны состоять (каждое) по крайней мере из десяти цифр.
Один из способов выбора p и q — воспользоваться Google и найти веб-сайт, на котором перечисляются крупные простые числа. Скажем, Primes Pages, который ведет Крис Колдуэлл из Университета Теннесси в Мартине. Выберите случайным образом два десятизначных простых числа. Вот пример такой парочки:
1 500 450 271 и 3 367 900 313.
Назовите их соответственно р и q. Вам придется перемножить их и получить точный ответ. Здесь может быть небольшая трудность, так как вы не сможете воспользоваться калькуляторами, Excel или Google, да и большинством любых других потребительских программ, поскольку они показывают ограниченное число значимых цифр. Один из вариантов — умножить вручную. Или использовать Wolfram Alpha. Введите
1 500 450 271 и 3 367 900 313
и вы получите точный ответ:
5 053 366 937 341 834 823.
Назовите это произведение N. Оно является одной из составляющих вашего общественного ключа. Другим компонентом является число, называемое е, произвольно выбранное и равное по длине, в идеале N, но которое не делится точно на произведение (р — 1) (q — 1). Я, возможно, запутал вас последним предложением, но пока об этом не беспокойтесь.
Во многих прикладных программах в качестве е шифровальщики выбирают простую тройку. Этот достаточно хороший вариант для многих целей и позволяет быстро шифровать.
Вы получили N и е, у вас теперь имеется все необходимое для решения задачи. Всего лишь нужно отправить эти два числа Пете, а также полное «Руководство для чайников по криптографии RSA». Пете необходимо вычислить
хe mod N,
где Х – это номер телефона. Поскольку в качестве e мы выбрали 3, часть слева — это х, возведенное в куб. Это будет число из 30 цифр. «Mod» указывает на деление по модулю, что означает, что вы разделите x³ на N и возьмете только остаток. Этот остаток должен быть в диапазоне от 0 до N — 1. Вполне вероятно, что будет число из 20 цифр. Это число является зашифрованным посланием, которое Петя отправит обратно вам.
Для решения этой задачи Пете необходимо возвести в куб число, и произвести деление. Важная часть инструкции может быть такой.
«Петя, я хочу, чтобы ты внимательно следовал этим инструкциям и не сомневался. Исходи из того, что мой телефонный номер — это обычное число из десяти цифр. Вначале необходимо, чтобы ты возвел в куб это число (умножь вначале его на само себя, а затем полученное произведение умножь еще раз на первоначальный номер). Ответ будет числом из 30 цифр, и оно должно быть точным. Выполни это умножение, даже если придется сделать это вручную, и дважды его проверь. Затем необходимо, чтобы ты осуществил самый длинный процесс деления за всю свою жизнь. Раздели полученный результат на число 5 053 366 937 341 834 823. Важно не ошибиться! Пришли мне только остаток этого деления. Важно, чтобы ты не прислал целую часть, а только остаток».
Затем кликни на маленький знак равенства, находящийся в правой части прямоугольника. Ответом будет, вероятно, число из 20 цифр, которое появится в прямоугольнике со словом Result (Результат). Пришли мне этот ответ, и только этот ответ».
Естественно, Катя прочитает эти инструкции, а также прочитает ответ Пети. Но она не сможет ничего понять. Она получила число из 20 цифр, которое, как она знает, является остатком куба телефонного номера, разделенного на 5053366937341834823, по модулю. Пока никто не придумал эффективного способа, позволяющего восстановить по остатку исходное число, в данном случае являющееся телефонным номером.
Можете ли вы предложить что-то еще лучше? Да, поскольку у вас есть секретный декодирующий ключ. Это d, инверсивное значение е mod (р — 1) (q — 1). Для его вычисления имеется удобный алгоритм, которым можно воспользоваться, конечно, при условии, что вы знаете два простых числа p и q, которые были использованы для получения N. (Вы ведь знаете их, потому что сами их выбрали, не забыли?)
Назовите кодированное число/сообщение, которое Петя отправил вам назад. Y. Его первоначальное сообщение было
Yd mod N.
Для определения этого значения нужно всего лишь ввести это в Wolfram Alpha (замените Y, d и N фактическими числами).
Катя знает N, поскольку оно было написано на карточке, которую вы попросили её передать Пете. Она знает Y, поскольку это число было указано в ответе Пети, отправленном вам. Но она не знает d, и у нее нет возможности его выяснить. Катя сталкивается с алгоритмической трудностью. При умножении двух чисел никаких сложностей ни у кого не возникнет, ведь этому все-таки в школе всех научили. А вот определить множитель, имея огромное число, гораздо сложнее.
Разбор по книге «Действительно ли Вы достаточно умны, чтобы работать в Google?»
IV Олимпиада по криптографии и математике
IV Олимпиада по криптографии и математике
список всех олимпиад по криптографии и математике
Задача 4.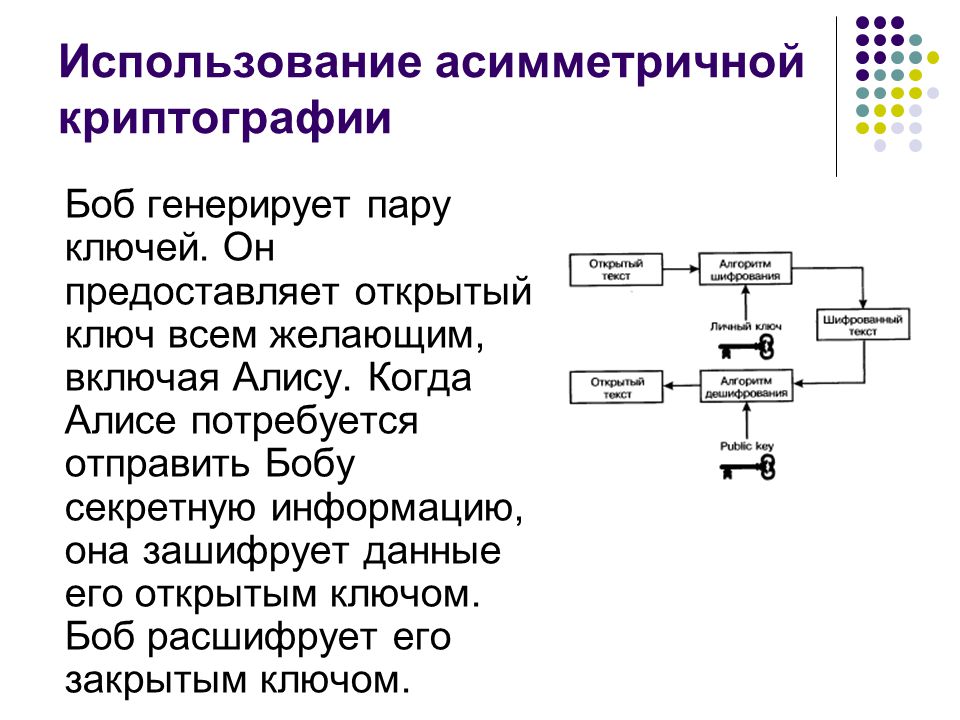
1.
Ключом шифра, называемого «решеткой», является прямоугольный трафарет размера 6× 10 клеток. В трафарете вырезаны 15 клеток так, что при наложении его на прямоугольный лист бумаги размера 6 × 10 клеток четырьмя возможными способами его вырезы полностью покрывают всю площадь листа.
Буквы сообщения (без пропусков) последовательно вписываются в вырезы трафарета (по строкам, в каждой строке слева направо) при каждом из четырех его возможных положений. Прочтите исходный текст, если после зашифрования на листе бумаги оказался следующий текст (на русском языке):
Задача 4.2.
Криптограмма
12 2 24 5 3 21 6 29 28 2 20 18 20 21 5 10 27 17 2 11 2 16 —
19 2 27 5 8 29 12 31 22 2 16, 19 2 19 5 17 29 8 29 6 29 16:
8 2 19 19 29 10 19 29 14 19 29 29 19 10 2 24 2 11 2 16
10 14 18 21 17 2 20 2 28 29 16 21 29 28 6 29 16.
получена заменой букв на числа (от 1 до 32) так, что разным буквам соответствуют разные числа. Отдельные слова разделены несколькими пробелами, буквы — одним пробелом, знаки препинания сохранены. Буквы «е» и «ё» не различаются. Прочтите четверостишие В. Высоцкого.
«Шифровальный диск» используется для зашифрования числовых сообщений. Он состоит из неподвижного диска и соосно вращающегося на нем диска меньшего диаметра. На обоих дисках нанесены цифры от 0 до 9, которые расположены в вершинах правильных 10-угольников, вписанных в диски.
Цифра X на неподвижном диске зашифровывается в цифру Y подвижного диска, лежащую на том же радиусе, что и X.
Для построения вписанного 10-угольника без транспортира надо уметь строить угол в 36◦. Попытайтесь вычислить с точностью до 0,1 значение какой-либо тригонометрической функции такого угла без таблиц и калькулятора.
Задача 4.4.
Зашифрование фразы на латинском языке осуществлено в два этапа. На первом этапе каждая буква текста заменяется на следующую в алфавитном порядке (последняя Z заменяется на первую A).
На втором этапе применяется шифр простой замены с неизвестным ключом. Его применение заключается в замене каждой буквы шифруемого текста буквой того же алфавита, при этом разные буквы заменяются разными буквами. Ключом такого шифра является таблица, в которой указано, какой буквой надо заменить каждую букву алфавита.
По данному шифртексту
OSZJX FXRE YOQJSZ RAYFJ
восстановите открытое сообщение, если известно, что для использованного (неизвестного) ключа результат шифрования не зависит от порядка выполнения указанных этапов для любого открытого сообщения. Пробелы в тексте разделяют слова.
Латинский алфавит состоит из следующих 24 букв:
A B C D E F G H I J L M N O P Q R S T U V X Y Z.
Задача 4.5.
Для проверки телетайпа, печатающего буквами русского алфавита
А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я
передан набор из 9 слов, содержащий все 33 буквы алфавита. В результате неисправности телетайпа на приемном конце получены слова
ГЪЙ АЭЕ БПРК ЕЖЩЮ НМЬЧ СЫЛЗ ШДУ ЦХОТ ЯФВИ
Восстановите исходный текст, если известно, что характер неисправности таков, что каждая буква заменяется буквой, отстоящей от нее в указанном алфавите не дальше, чем на две буквы. Например, буква Б может перейти в одну из букв {А, Б, В, Г}.
Задача 4.6.
Исходное сообщение из букв русского алфавита преобразуется в числовое сообщение заменой каждой его буквы числом по следующей таблице:
| A | Б | В | Г | Д | Е | Ж | З | И | К |
| 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 |
| Л | М | Н | О | П | Р | С | Т | У | Ф |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| X | Ц | Ч | Ш | Щ | Ь | Ы | Э | Ю | Я |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
Для зашифрования полученного числового сообщения используется шифрующий отрезок последовательности подходящей длины, начинающийся с .
При зашифровании каждое число числового сообщения складывается с соответствующим числом шифрующего отрезка. Затем вычисляется остаток от деления полученной суммы на 30, который по данной таблице заменяется буквой. Восстановите сообщение КЕНЗЭРЕ, если шифрующий отрезок взят из последовательности, у которой и для любого натурального .
Задача 4.7
Чтобы запомнить периодически меняющийся пароль в ЭВМ, математики придумали следующий способ. При известном числе a (например, номере месяца в году), пароль представляет собой первые шесть цифр наименьшего решения уравнения . (Число меньшей значности дополняется справа необходимым числом нулей.)
Решите такое уравнение при произвольном .
список всех олимпиад по криптографии и математике
1.2. Основные задачи криптографии.
Задача криптографии, т.е. тайная передача, возникает только для информации, которая нуждается в защите. В таких случаях говорят, что информация содержит тайну или является защищаемой, приватной, конфиденциальной, секретной. Для наиболее типичных, часто встречающихся ситуаций такого типа введены даже специальные понятия:
государственная тайна;
военная тайна;
коммерческая тайна;
юридическая тайна;
врачебная тайна и т. д.
Далее мы будем говорить о защищаемой информации, имея в виду следующие признаки такой информации:
имеется какой-то определенный круг законных пользователей, которые имеют право владеть этой информацией;
имеются незаконные пользователи, которые стремятся овладеть этой информацией с тем, чтобы обратить ее себе во благо, а законным пользователям во вред.
1.3 Выводы по разделу 1.
Криптография — это набор методов защиты информационных взаимодействий от отклонений от их нормального, штатного протекания, вызванных злоумышленными действиями различных субъектов, методов, базирующихся на секретных алгоритмах преобразования информации, включая алгоритмы, не являющиеся собственно секретными, но использующие секретные параметры. Исторически первой задачей криптографии была защита передаваемых текстовых сообщений от несанкционированного ознакомления с их содержанием, что нашло отражение в самом названии этой дисциплины, эта защита базируется на использовании «секретного языка», известного только отправителю и получателю, все методы шифрования являются лишь развитием этой философской идеи. С усложнением информационных взаимодействий в человеческом обществе возникли и продолжают возникать новые задачи по их защите, некоторые из них были решены в рамках криптографии, что потребовало развития принципиально новых подходов и методов.
2. Криптографические средства защиты.
Криптографическими средствами защиты называются специальные средства и методы преобразования информации, в результате которых маскируется ее содержание. Основными видами криптографического закрытия являются шифрование и кодирование защищаемых данных. При этом шифрование есть такой вид закрытия, при котором самостоятельному преобразованию подвергается каждый символ закрываемых данных; при кодировании защищаемые данные делятся на блоки, имеющие смысловое значение, и каждый такой блок заменяется цифровым, буквенным или комбинированным кодом. При этом используется несколько различных систем шифрования: заменой, перестановкой, гаммированием, аналитическим преобразованием шифруемых данных. Широкое распространение получили комбинированные шифры, когда исходный текст последовательно преобразуется с использованием двух или даже трех различных шифров.
2.1 Принцыпы работы Криптосистемы.
Типичный пример изображения ситуации, в которой возникает задача криптографии (шифрования) изображён на рисунке №1:
Рис.
№1
На рисунке № 1 А и В — законные пользователи защищённой информации, они хотят обмениваться информацией по общедоступному каналу связи. П — незаконный пользователь (противник, хакер), который хочет перехватывать передаваемые по каналу связи сообщения и попытаться извлечь из них интересную для него информацию. Эту простую схему можно считать моделью типичной ситуации, в которой применяются криптографические методы защиты информации или просто шифрование.
Исторически в криптографии закрепились некоторые военные слова (противник, атака на шифр и др.). Они наиболее точно отражают смысл соответствующих криптографических понятий. Вместе с тем широко известная военная терминология, основанная на понятии кода (военно-морские коды, коды Генерального штаба, кодовые книги, кодобозначения и т. п.), уже не применяется в теоретической криптографии. Дело в том, что за последние десятилетия сформировалась теория кодирования — большое научное направление, которое разрабатывает и изучает методы защиты информации от случайных искажений в каналах связи.
Криптография
занимается методами преобразования
информации, которые бы не позволили
противнику извлечь ее из перехватываемых
сообщений. При этом по каналу связи
передается уже не сама защищаемая
информация, а результат ее преобразования
с помощью шифра, и для противника
возникает сложная задача вскрытия
шифра. Вскрытие (взламывание) шифра —
процесс получения защищаемой информации
из шифрованного сообщения без знания
примененного шифра. Противник может
пытаться не получить, а уничтожить или
модифицировать защищаемую информацию
в процессе ее передачи. Это — совсем
другой тип угроз для информация, отличный
от перехвата и вскрытия шифра. Для защиты
от таких угроз разрабатываются свои
специфические методы. Следовательно,
на пути от одного законного пользователя
к другому информация должна защищаться
различными способами, противостоящими
различным угрозам. Возникает ситуация
цепи из разнотипных звеньев, которая
защищает информацию.
Естественно,
противник будет стремиться найти самое
слабое звено, чтобы с наименьшими
затратами добраться до информации. А
значит, и законные пользователи должны
учитывать это обстоятельство в своей
стратегии защиты: бессмысленно делать
какое-то звено очень прочным, если есть
заведомо более слабые звенья («принцип
равнопрочности защиты»).
Придумывание хорошего шифра дело трудоемкое. Поэтому желательно увеличить время жизни хорошего шифра и использовать его для шифрования как можно большего количества сообщений. Но при этом возникает опасность, что противник уже разгадал (вскрыл) шифр и читает защищаемую информацию. Если же в шифре сеть сменный ключ то, заменив ключ, можно сделать так, что разработанные противником методы уже не дают эффекта.
Разработка криптографических систем с открытым ключом, основанных на обобщении задачи о ранце Текст научной статьи по специальности «Математика»
УДК 004.056.55
М. И. Вахрушев, Е. А. Загурских
Новосибирский государственный университет ул. Пирогова, 1, Новосибирск, 630090, Россия
[email protected], [email protected]
РАЗРАБОТКА
КРИПТОГРАФИЧЕСКИХ СИСТЕМ С ОТКРЫТЫМ КЛЮЧОМ, ОСНОВАННЫХ НА ОБОБЩЕНИИ ЗАДАЧИ О РАНЦЕ
Развитие квантовых компьютеров ставит под угрозу множество распространенных на данный момент криптосистем, основанных на задачах факторизации, дискретного логарифмирования и других, которые могут быть решены за полиномиальное время на квантовом компьютере.
Однако на данный момент не предложено алгоритмов, позволяющих за полиномиальное время решать №-полные задачи квантовыми компьютерами.
Мы рассматриваем две криптосистемы с открытым ключом, основанные на №-полных задачах о сумме подмножеств и целочисленного программирования.
Ключевые слова: асимметричная криптография, постквантовая криптография, рюкзачная криптография, №-полнота, задача о сумме подмножеств.
Введение
В данной работе рассматриваются два подхода к построению систем шифрования с открытым ключом на основе методов, использующих некоторые обобщения задач subset sum и целочисленного программирования.
Обоснование стойкости предлагаемых алгоритмов основано на том, что в результате шифрования получается система линейных уравнений, в которой число уравнений меньше, чем число неизвестных, к тому же на неизвестные налагаются ограничения. Доказано, что задача решения таких уравнений NP-полна [1]. На данный момент не существует алгоритмов, позволяющих решать данную задачу эффективно с помощью квантовых компьютеров, поэтому предлагаемые алгоритмы являются алгоритмами постквантовой криптографии.
Задача subset sum
Задача subset sum заключается в поиске такого непустого подмножества некоторого набора чисел, что сумма чисел этого подмножества равна нулю. Эту задачу можно считать частным случаем задачи о ранце [2]. В данной статье будем рассматривать эквивалентную subset sum задачу, заключающуюся в нахождении подмножества, сумма элементов которого равна некоторому заданному числу s. Несмотря на то, что обе эти задачи являются NP-полными, существуют такие наборы чисел, для которых задачи легко решаются за полиномиальное время.
В данном параграфе рассматриваются методы построения таких наборов целых положительных чисел, что всевозможные суммы различных чисел не совпадают.
Другими словами,
Вахрушев М. И., Загурских Е. А. Разработка криптографических систем с открытым ключом, основанных на обобщении задачи о ранце // Вестн. Новосиб. гос. ун-та. Серия: Информационные технологии. 2016. Т. 14, № 4. С. 31-38.
ISSN 1818-7900. Вестник НГУ. Серия: Информационные технологии. 2016. Том 14, № 4 © М. И. Вахрушев, Е. А. Загурских, 2016
если нам известно некоторое число, то можно однозначно, с точностью до перестановки, найти те числа, сумма которых равна данному числу. Для таких наборов чисел легко решить задачу subset sum.
Один из вариантов такого набора — сверхвозрастающая (супервозрастающая) последовательность [3], однако для последовательностей такого вида имеет место проблема, заключающаяся в том, что представимые числа расположены очень редко. Приведем другой алгоритм построения наборов чисел, избавленных от данного недостатка.
Алгоритм 1
Будем одновременно строить две последовательности: сам набор чисел и набор всех возможных сумм элементов первого набора.
1. Прежде всего, в последовательность сумм записывается число 0, которое означает, что для составления суммы никаких чисел не берется.
2. Теперь выберем первое натуральное число X. Множество возможных сумм на данном этапе: {0, X}.
3. Далее будем последовательно, до момента достижения необходимой длины последовательности, выбирать некоторое число, не представимое в виде сумм предыдущих и большее любого из уже выбранных чисел.
Заметим, что всевозможные суммы различных чисел полученного набора не совпадают по построению и получившаяся последовательность не будет обязательно супервозрастаю-щей.
Кроме того, из построенных таким образом наборов чисел можно строить другие, воспользовавшись сильным модульным умножением [4].
Приведем два алгоритма построения новых последовательностей с помощью сильного модульного умножения. Пусть дана некоторая последовательность целых положительных чисел {aj} и последовательность возможных сумм ее элементов {¿j}. Выберем некоторое число z, большее максимальной возможной суммы, и посчитаем количество обратимых элементов по модулю данного числа, воспользовавшись функцией Эйлера. Пусть существует N обратимых элементов, тогда с помощью модуля z мы можем построить N — 1 новую последовательность каждым из алгоритмов (не N, так как среди обратимых элементов будет 1). Рассмотрим предлагаемые алгоритмы:
Алгоритм 2.1
Выбираем любой обратимый элемент x по модулю z и преобразовываем последовательность {aj} в {ax mod(z)}, а последовательность сумм {¿j} пересчитываем заново, с учетом изменений в исходной последовательности.
Алгоритм 2.2
Выбираем любой обратимый элемент x по модулю z и добавляем к последовательности {aj} последовательность {ax mod(z)}, тем самым удлиняя исходный набор чисел в два раза. Последовательность сумм {¿j} также необходимо пересчитать. Далее применяем Алгоритм 2.1 к новой последовательности и на выходе получаем новый набор чисел.
Пример 1
Ниже приводится пример построения набора чисел из 4 элементов с помощью Алгоритма 1:
• Пусть выполнен первый пункт алгоритма и на втором этапе в первый раз было выбрано число 5, тогда текущая последовательность чисел — {5} и возможные суммы — {0, 5}. Будем выполнять третий пункт алгоритма.
(4×11) = 2 X 10 = 20, значит можно изготовить 19 новых последовательностей (не 20, т.к. 1×1 = 1mod(44)). Например, рассмотрим число 5, обратным является 9, т.к 5×9 = 1mod(44). Значит относительно сильного модульного умножения на 5 последовательность {5, 7, 11, 14} перейдет в последовательность {25, 35, 11, 26}, а последовательность сумм перейдет в новую — {0, 11, 25, 26, 35, 36, 37, 46, 51, 60, 61, 62, 71, 72, 86, 97}.
Воспользуемся Алгоритмом 2.2 построения нового набора чисел. Выберем число, большее 37, например, 39. Тогда промежуточной последовательностью будет {5,7,11,14,5 X 39,7 X 39,11 X 39,14 X 39} = {5,7,11,14,195,273,429,546}. Максимальная сумма равна 1480. Заметим, что 31 X 48 = 1mod(1487) и 1480 < 1487. Применим сильное модульное умножение и получим новую последовательность {0, 240, 336, 528, 672, 438, 1208, 1261, 929}, которая имеет длину в два раза больше, чем исходная.
Прямой подход
Построение ключей
Рассмотрим матрицу B Е ZXn, k < n/2, строки которой построены следующим образом. Пусть N=[n/k], тогда первые (i-1) Nэлементов i-й строки (i =1…k) — случайные, следующие N элементов — последовательность, являющаяся легко разрешимой для задачи subset sum, например, построенная одним из вышеописанных алгоритмов, остальные элементы — нулевые. Система уравнений вида Вх = у (1) при x Е {0,1}n либо не имеет решения, либо имеет единственное решение, которое находится за полиномиальное время. По построению B эту систему легко решить следующим образом: из первого уравнения находим первые N бит сообщения путем последовательного деления с остатком правой части уравнения на коэффициенты, начиная с наибольшего элемента легко разрешимой последовательности. Частное от каждого деления будет являться соответствующим битом сообщения, а остаток -делимым, используемым при вычислении следующего бита, и т.
, х9, х10 во втором. Таким образом,
В = (2 3 7 14 27 0 0 0 0 0 \ 13 12 7 2 1 4 5 10 21 41
Система уравнений Вх = Ь имеет вид
2хх + 3х2 + 7х3 + 14х4 + 27х5 + 0х6 + 0х7 + 0х8 + 0х9 + 0х10 = Ьг 3хх + 12х2 + 7х3 + 2х4 + 1х5 +4х6 + 5х7 + 10х8 + 21х9 + 41х10 = ь2
Добавив еще два произвольных уравнения, получаем матрицу
А =
3 7 14 27 0 0 0 0 0
12 7 2 1 4 5 10 21 4
4 1 40 2 3 7 2 3 21
11 3 2 10 7 4 1 1 8
Система уравнений Ах = Ь представляет собой систему вида (2)
2х1 + 3х2 + 7х3 + 14х4 + 27х5 + 0х6 + 0х7 + 0х8 + 0х9 + 0х10 = Ь1 3хх + 12х2 + 7х3 + 2х4 + 1х5 +4х6 + 5х7 + 10х8 + 21х9 + 41х10 = ь2 5хх + 4х2 + 1х3 +40х4 + 12х5 + 3х6 + 7х7 + 2х8 + 3х9 + 21х10 = ь3 0хг + 11х2 + 3х3 + 2х4 + 10х5 + 7х6 + 4х7 + 1х8 + 11х9 + 8х10 = Ь4
Следующим шагом находим максимальные значения для правых частей системы уравнений: т1=тах(Ь1)=53, т2=тах(Ь2)=106, т3=тах(Ь3)=98, т4=тах(Ь4)=57, тах{ти т2, т3, т4}=106. Возьмем простоер=149>106 и матрицу Н:
Матрица обратима, так как ёв((Н)=114 и gcd(106, 149)=1. Теперь получим матрицу Я = НАтойр:
Таким образом, построенная матрица Я является открытым ключом, а матрицы В, А и Н -закрытым.
Шифрование
Пусть необходимо зашифровать сообщение е=(1, 0, 0, 1, 0, 1, 1, 1, 0, 0).
Ц, ее определитель det=15. Если планируется решать данную систему в целых числах, то желательно, чтобы определитель равнялся 1. Этого можно добиться выбором другого набора случайных чисел во второй строчке уравнения.
Теперь применим стандартный подход к решению этой системы. Построим матрицу Ь с определителем 1 такую, что и = ЬС — верхнетреугольная матрица. Напимер, при Ь =
С3 2) получим: у=(0 1).
Умножим систему (5) слева на матрицу L, получим эквивалентную систему уравнений (6):
1хх + 9х2 + 0х3 — 12х4 — 26х5 +4х6 + 5х7 + 10х8 + 17х9 + 41х10 = 0 0хг + 15х2 -7Х3 — 38Х4 — 79Х5 + 8Х6 + 10Х7 + 20Х8 + 34Х9 + 82Х10 = 0
В данной системе во втором уравнении есть два взаимно простых числа -7 и 10 при x3 и x7 соответственно. Это означает, что переменные x2, x4, x5, x6, x8, x9, x10 можно выбирать произвольно. Для упрощения примера выберем x2=x4=x5=x6=x8=x9=x10=1, подставим эти значения во второе уравнение системы и получим уравнение 7х3 — 10х7 = 42.
Используя алгоритм Евклида найдем переменные x3 и x7: x3=6, x7=0. Теперь подставим в первое уравнение системы (3) полученные значения и найдем x1=-78. В результате получим первое решение однородной системы: u1=(-43,1, 6,1,1,1, 0,1,1, 1).
Повторив описанные выше действия для других пар взаимно простых чисел из коэффициентов второго уравнения системы (6) найдем полный набор решений системы однородных уравнений (5). Кроме того, можно рассмотреть матрицу С при других переменных системы, построить для нее матрицу L и повторить дальнейшие рассуждения. Если же уравнений в исходной системе больше двух, то рассуждения аналогичны.
Пусть N=2, тогда нужно найти еще одно решение.
В этот раз рассмотрим пару взаимно простых чисел 15 и 8 при x2 и x6 и, повторив вышеописанные действия, найдем решение U2= =(-33, 6, 1, 1, 1, -14,1,1,1,1).
Полученные вектора u1, u2 ортогональны векторам-строкам матрицы B по построению. Далее выберем M=3 и построим вектора открытого ключа w1, w2, w3, выбрав случайные вектора ах = (1,2,3) и а2 = (5,6,7): w=(-208, 31, 11, 6, 6, -69, 5, 6, 6, 6), W2=(-284, 38, 18, 8, 8, -82, 6, 8, 8, 8), w3=(-360, 45, 25, 10,10, -95, 7, 10, 10,10). Эти вектора также ортогональны векторам a1, a2 и являются элементами открытого ключа. В то же время матрица A — секретный ключ.
Шифрование
Пусть сообщением является вектор e=(0,1, 0,1, 0,1, 0,1, 0, 1). Выберем случайно 4 целых числа А1 = 10, А2 = 2,Л,3 = 5 и вычислим шифротекст:
с = A1w1 + A2w2 +A3w3 + е В данном примере получим c=(-3369, 429, 293, 84, 83, -951,167, 84, 83, 83).
Дешифрование
Вычисляем
у = Ас = A1Aw1 +A2Aw2 +A3Aw3 + Ае = Ае
Решая систему уравнений Ае = у = (17,69) согласно методу, описанному в параграфе 2, находим вектор зашифрованного сообщения e=(0,1, 0,1, 0,1, 0,1, 0, 1).
Заметим, что для упрощения примера были выбраны заведомо неудачные «случайные» числа на разных этапах алгоритма, вследствие чего по шифротексту можно догадаться об элементах сообщения и секретного ключа.
Основным недостатком описанного подхода является рост размера ключа, поскольку все вычисления проводятся в целых числах. Однако эту проблему можно устранить, если выполнять все вычисления по некоторому модулю p, выбранному больше максимальной возможной суммы последовательности чисел, состоящей из коэффициентов уравнений системы.
Заключение
В данной работе предложено два способа построения криптосистем, основанных на обобщении частного случая задачи о ранце — задачи subset sum. Рассмотренные подходы ос-
нованы на том факте, что кольцо целых чисел является евклидовым. Таким образом, возможно построение криптографических систем на базе других евклидовых колец, например, на базе кольца многочленов с коэффициентами из конечного поля. Однако это тема для отдельных исследований, не рассматриваемых в данной работе.
Список литературы
1. Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и анализ. 3-е изд. М.: Вильямс, 2013. 1328 с.
2. Martello S., Toth P. Knapsack problems: Algorithms and computer interpretations. Wiley-Interscience, 1990. 306 с.
3. Шнайер Б. Прикладная криптография: протоколы, алгоритмы, исходные тексты на языке Си. М.: Триумф, 2002. 610 c.
4. СаломааА. Криптография с открытым ключом. M.: Мир, 1995. 320 с.
Материал поступил в редколлегию 23.08.2016
M. I. Vakhrushev, E. A. Zagurskikh
Novosibirsk State University 1 Pirogov Str., Novosibirsk, 630090, Russian Federation
[email protected], [email protected]
DESIGN OF KNAPSACK CRYPTOSYSTEMS
The development of quantum computers endangers the great number modern cryptosystems based on factorization problem, discrete logarithm problem and other, which can be solved in polynomial time on a quantum computer.
However, quantum computing algorithms can’t efficiently solve NP-hard problems at present. In this paper, we consider two public key cryptosystems based on NP-hard problems: subset sum and integer programming.
Keywords: post-quantum cryptography, knapsack public-key cryptosystem, subset sum problem, NP-hard, knapsack problem.
References
1. T. Cormen, C. Leiserson, R. Rivest, C. Stein. Introduction to Algorithms. 3rd. MIT Press, 2009. 1312 p.
2. S. Martello, P. Toth. Knapsack problems: Algorithms and computer interpretations. Wiley-Interscience, 1990. 306 p.
3. B. Schneier. Applied Cryptography: Protocols, Algorithms, and Source Code in C. John Wiley & Sons, 1996. 784 p.
4. A. Salomaa. Public-Key Cryptography — Springer Science & Business Media, 1996. 275 p.
Задача о рюкзаке в криптографии
1. История.
(History) Проблема рюкзака лежит в основе первого алгоритма асимметричного шифрования или шифрования с открытым ключом. идея криптографии с открытыми ключами была выдвинута американской криптографии Уитфилда Диффи, Мартином Хеллманом и независимо Ральфом Меркле. в первый раз было введено Диффи и Хеллманом на Национальной компьютерной конференции англ. National Computer Conference (Национальной Компьютерной Конференции) в 1976 году в том же году была издана их совместная работа на эту тему — «New Directions in Cryptography» Рус. «Новые направления в криптографии». Меркле Статье «Secure Communication Over Insecure Channels» Рус. «Безопасная связь по незащищённым каналам» был опубликован в 1978 году.
новизной по отношению к распространенным в то время симметричных криптосистем является использование пары ключей — закрытого и открытого англ. public key (открытый ключ), PK пользовательский. секретный ключ используется для расшифровки информации, пользователь должен скрывать, тогда как открытый ключ нужен только для шифрования может быть открытым. во многих криптосистем с секретным ключом вам открытый ключ.
Первый алгоритм шифрования на основе задачи о ранце были разработаны Меркл и Хеллман в 1978 году и был назван «Алгоритм Меркла-Хеллмана». он был опубликован в одноступенчатых англ. singly-iterated (поодиночке-повторяемых) и многоступенчатой гидравлической версии на английском языке. multiply-iterated (умножить-повторяемых). алгоритм мог быть использован только для шифрования, но израильский криптоаналитик Ади Шамир и адаптировали его для использования в цифровых подписях. после опубликования схемы Меркл предложил вознаграждение в 100 долларов тому, кто успешно осуществил взлом одноэтапный алгоритм. В 1982 году Шамир провел успешную атаку и получил обещанное вознаграждение. но даже после уплаты Меркле был уверен в надежности многоступенчатой гидравлической системы и предложил 1000 долларов в случае успешного взлома. В 1984 году американский математик Эрнест Брикелл удалось осуществить взлом за сорок этапе вариант немного более за 1 час на автомобиле Cray-1 (Крэй-1).
Независимо друг от друга в 1980 году американский математик Грэм Рон и Ади Шамир нашли способ повысить безопасность схемы Меркла-Хеллмана, но в 1983 году полученный схема Грэм-Шамир был взломан американский ученый Леонард Адлеман. однако, поиск изменений, лишен недостатков схемы Меркла-Хеллмана, продолжил. В 1985 году британский профессор Родни Гудман и американскому инженеру Энтони Маколи создал схему, основанную на модульном рюкзаки с тайной лазейки, которые не основаны на векторах servosystemer, и используя китайскую теорему об остатках.
Впоследствии выяснилось, что схема уязвима для атаки, основанные на поиске тайных лазеек.
но в 1990 году Валттери Ниеми предложена новая схема, основанная на той же задачи модульный рюкзак. он был взломан в следующем году Чи е Антуана Жу, и Жак Стерн независимо друг от друга, несколько разных методов. в дополнение к использованию модульные рюкзаки были попытки использовать другие виды рюкзак.
Так, в 1986 году Харальд Niederreiter опубликовал рюкзачные системы на основе алгебраической теории кодирования, который позже был взломан, и в 1988 году Масакацу Мории и Масао Касахара разработана криптосистема, используя мультипликативный рюкзак. идея была хорошая и во время работы системы на мультипликативный рюкзаки не треснул.
В 2001 году Шинья Киучи, Ясуюки Мураками и Масао Касахара предложения по усовершенствованию схемы Мориа-Касахара на основе мультипликатора рюкзаков с использованием алгоритма Schalkwijk.
Также успешной была идея Хусейн Али Хусейн, Джафар Вади Абдул сад М. Халифа, который предложил в 1991 году многоступенчатая рюкзачные системы инж. multistage trapdoor knapsack cryptosystem (многоступенчатый люк ранцевая криптосистема). Она включает в себя векторные ранец для каждого этапа, и вывод зашифрованного текста после каждого этапа алгоритма используется в качестве входного текста на этапе успешной атаки по этой схеме не известно на 2001 год.
В Минхуа Цюй и Скотт Vanston в 1992 году предложена гибридная криптосистема, которая основывается прежде всего на проблему упаковки, но также включает в себя логарифмический подпись. В 1994 году Р. Блэкберн, Мерфи, Шон и Жак Стерн показал, что упрощенный вариант Ву-Ватсон. криптосистема неуверенно. эти криптосистемы были более тщательно изучены Фонг Нгуен и Жак Стерн в 1997 году.
Продолжение улучшения классического алгоритма, Меркле-Хеллмана. В 1994 году Ортон предложена модификация многоступенчатого гидравлического Меркле-Хеллмана схема, но после двух лет она была взломана Риттер.
В 1995 году были предложены два новых подхода к проблеме. во-первых, на основе диофантовых уравнений принадлежит Jusino Лин, Чжан Кьянчано, будь Catunu.
почти сразу лай, Zisun и Блэкберн, Мерфи, Шон С. Патерсон. Г, независимо друг от друга показали, что эта криптосистема не является безопасной.
Второй подход основан на проблеме мультипликативный рюкзак был предложен Дэвидом Наккаш и Жак Стерн. Наккаш и Штерн предлагал 1024 ДМ кто-то, кто успешно взломает их cryptoscheme, но информация о том, что кто-то получил эту награду еще не было на 2001 год.
В 1996 году Kunikazu и Кобаяси Масаки Кимура предложил улучшить рюкзачные системы на основе новой концепции, где отправитель может выбрать ключ шифрования ключей. после двух лет, Hidenori Танаки и Hatsukazu Kuakata показал, что система является потенциально небезопасной.
Последний вариант был предложен алгоритм Б. и Шора Р. Л. Ривест в 2006 году. Алгоритм В 2002 году Chor-Rivest (Чор-Ривест) считался безопасным.
В 2015 году сообщил, что Натан Хэмлин и Уильям Уэбб из Университета штата Вашингтон создали алгоритм ранца без недостатков предыдущих релизов.
В будущем, было высказано мнение, что многие государственные ключевые алгоритмы, не основанные на ранцевых систем. самые известные из них: RSA (ОГА), EIGamal и Rabin (Рабин). они могут быть использованы для шифрования и для цифровой подписи. однако они медленные и не подходят для быстрого шифрования / расшифровки больших объемов сообщений. решением этой проблемы является гибридный криптография, шифрование сообщений с помощью симметричного шифрования со случайным ключом и открытым ключом алгоритм используется для шифрования случайного ключа сессии.
Лекции
Конспекты
| Темы для семинара
|
задачи декодирования – Новости – Московский институт электроники и математики им. А.Н. Тихонова – Национальный исследовательский университет «Высшая школа экономики»
24 января 2019 г. в рамках научного семинара «Коды, исправляющие ошибки, и пост-квантовая криптография» выступил д.т.н., профессор, научный руководитель, и.о. директора МИЭМ НИУ ВШЭ Евгений Крук, основной темой доклада которого являлось обсуждение криптосистем, построенных на основе решения задачи декодирования произвольного кода, исправляющего ошибки.
Евгений Крук является одним из ведущих российских ученых в области помехоустойчивого кодирования, компьютерной безопасности и кодовой криптографии, руководит в МИЭМ научной лабораторией Интернета вещей и киберфизических систем.
Доклад содержал краткое введение в кодовую криптографию и описание двух основных кодовых криптосистем — системы Мак-Элиса и системы Нидеррайтера. Данные системы, разработанные на основе теории алгебраического кодирования, сегодня являются уже классическими, а принципы их работы лежат в основе целого класса последующих разработок. Основой стойкости кодовой криптографии является задача декодирования линейных кодов (общая задача декодирования является NP-сложной).
Система Мак-Элиса — первая криптосистема с открытыми ключами, разработанная в 1978 году, использующая в процессе шифрования порождающую матрицу линейного кода.
Система Нидеррайтера — криптосистема с открытыми ключами, разработанная в 1986 году. В отличие от криптосистемы Мак-Элиса, в криптосистеме Нидеррайтера используется проверочная матрица кода.
Обе системы не получили широкого распространения в криптографических приложениях, но в то же время являются кандидатами для пост -квантовой криптографии, так как устойчивы к атаке с использованием квантового компьютера.
Основным препятствием для внедрения кодовых криптосистем является большой размер ключей. Поэтому, после рассмотрения базовых криптосистем, участники семинара обсудили их возможные модификации, позволяющие уменьшить ключ без потери криптостойкости.
В конце доклада была рассмотрена атака Зорге на одну из предложенных модификаций системы Мак-Элиса. В результате было показано, что данная модификация фактически не позволяет уменьшить ключ, поскольку задача вскрытия модифицированной системы может быть сведена к решению задачи вскрытия классической системы Мак-Элиса.
Как показало активное обсуждение темы семинара, данная проблематика интересна участникам и дает исследователям широкое поле для реализации своих идей и получения новых результатов.
Cryptopals Crypto Challenges
Добро пожаловать на вызов
Незавершенные работы.
На этом сайте будут размещены все восемь наборов наших криптовалютных задач, с решения на большинстве основных языков.
Но: пока нет. Если бы мы ждали, чтобы нажать «опубликовать», пока все был здесь, возможно, мы будем писать это в 2015 году. Итак, мы публикуем как мы идем.В частности: дайте нам немного времени на задачу решения.
Мы не можем представить их лучше, чем Мацей Цегловски сделал, так что сначала прочтите этот пост в блоге.
Мы собрали сборник из 48 упражнений, демонстрирующих атаки на реальные криптовалюты.
Это другой способ узнать о криптографии, чем занятия или чтение книги. Мы даем вам проблемы, которые нужно решить. Они проистекают из недостатков реальных систем и современных криптографических конструкций.Мы даем вам достаточно информации, чтобы самостоятельно изучить основные концепции криптографии. Когда вы закончите, вы не только узнаете много нового о том, как построены криптосистемы, но также поймете, как они атакуются.
Каковы правила?
Нет! В течение нескольких лет мы решали эти задачи по электронной почте и просили участников не сообщать их результаты. Система чести сработала прекрасно! Но теперь мы готовы отложить церемонию и просто опубликуйте задачи, чтобы каждый мог поработать над ними.
Сколько математики мне нужно знать?
Если у вас возникнут проблемы с математикой в этих задачах, вы сможете найти местного девятиклассника, который поможет вам. Оказывается, многие современные крипто-атаки не требуют сложной математики.
Сколько криптовалюты мне нужно знать?
Никто. В этом-то и дело.
Итак, что мне нужно знать?
Вы захотите уметь грамотно писать код на любом языке.
Мы получили заявки на C, C ++, Python, Ruby, Perl, Visual Basic, X86 Assembly, Haskell и Lisp. Удивите нас другим языком. Наш друг Мачей говорит, что эти задачи — хороший способ выучить новый язык, так что, возможно, сейчас самое время заняться Clojure или Rust.
Чего мне ожидать?
Сейчас у нас восемь наборов. Они становятся все труднее. Опять же: они основаны на реальных уязвимостях. Ни одна из них не является «головоломкой». Они не предназначены для того, чтобы сбивать вас с толку.Однако некоторые из атак являются умными, и если вы не знакомы с крипто-хитростью … что ж, вам должно понравиться разгадывать головоломки. Признание хип-хопа MTV начала 90-х тоже не повредит.
Можете ли вы дать нам длинное снисходительное описание того, почему вы выбрали именно это?
Оказывается, можем.
Если вы еще не так хорошо знакомы с криптографией или если вы знакомы в основном с такими вещами, как прикладная криптография, этот факт может вас удивить: большая часть криптографии фатально взломана.Системы, на которые мы полагаемся сегодня, и о которых не известно, что они сломаны до смертельного исхода, просто ждут, чтобы их сломали. Никто не уверен, что TLS 1.2, SSH 2 или OTR останутся безопасными, как было задумано.
Текущее состояние криптографической безопасности программного обеспечения аналогично состоянию безопасности программного обеспечения в 1990-х годах. В частности: примерно до 1995 года не было общепризнанным фактом, что программное обеспечение, созданное людьми, может иметь проблемы со счетом. В результате никто не мог правильно определить размер буфера, и человечество потратило миллиарды долларов на очистку после полутора десятилетий аварийных исправлений уязвимостей, связанных с повреждением памяти.
Подсчет — не сложная задача. Но криптография есть. Есть всего несколько вещей, которые вы можете испортить, чтобы получить неверный размер буфера.
Есть десятки, а может быть, и сотни непонятных мелочей, которые вы можете сделать, чтобы взять криптосистему, которая должна быть защищена даже от противника с большим количеством ядер ЦП, чем атомов в солнечной системе, и сделать ее решаемой с помощью сценария Perl и 15 секунд. . Не верьте нам на слово: решайте задачи, и вы увидите.
Люди уже «знают» это, но на самом деле они этого не знают, и мы думаем, что причина этого в том, что очень немногие люди на самом деле знают, как реализовать самые известные атаки.Так что напишите нам, и мы проведем для вас экскурсию по ним.
Как мне начать?
Начни здесь!
Кто это сделал?
- Томас Птачек (@tqbf)
- Шон Девлин (@spdevlin)
- Алекс Бальдуччи (@iamalexalright)
- Марцин Вельгошевский (@marcinw)
Криптопалы обслуживаются и расширяются (начиная с Сета 8) Шоном Девлином совместно с командой службы криптографии в NCC Group.
Мы не смогли бы сделать это без помощи еще нескольких человек. Примерно в порядке влияние:
- Нейт Лоусон научил нас практически всему, что мы знаем о криптографии.
- Тревор Перрин научил Нейта кое-чему. Я могу рассказать вам довольно интересную историю о том, как Тревор интеллектуальное происхождение каждой успешной атаки на TLS за последние 5 лет.
- Тай Дуонг и Джулиано Риццо — крестные отцы практического криптографического программного обеспечения. безопасность.Некоторые вещи в этом испытании не имели для нас смысла до тех пор, пока не вышли тайский и Джулиано использовал их в распространенном программном обеспечении.
Юридический
Отдельные материалы упражнений принадлежат их автору и могут распространяться или не распространяться по лицензии с открытым исходным кодом.
Практическая криптография
Хотя большинство людей заявляют, что они не знакомы с криптографией
, они часто знакомы с концепцией шифров, независимо от того, осознают ли они это на самом деле.
Шифры, возможно, являются краеугольным камнем криптографии. В общем, шифр — это просто набор шагов (алгоритм) для выполнения как шифрования, так и соответствующего дешифрования.
Несмотря на кажущуюся относительно простой концепцию, шифры играют решающую роль в современных технологиях. Технологии связи (включая Интернет , мобильные телефоны , цифровое телевидение или даже банкоматов ) полагаются на шифры для обеспечения как безопасности, так и конфиденциальности.
Хотя большинство людей заявляют, что они не знакомы с криптографией
, они часто знакомы с концепцией шифров, независимо от того, осознают ли они это на самом деле. В последних фильмах, таких как Код да Винчи
и Национальное лечение: Книга секретов
, сюжеты сосредоточены вокруг криптографии и шифров, доводя эти концепции до широкой публики.
В этом разделе (вполне уместно) рассматриваются отдельные шифры и алгоритмы.Они были разделены в зависимости от их эпохи и категории (т.е. , когда они использовали и , как они работают ). Если вы ищете справочное руководство, обратитесь к алфавитному списку справа, в противном случае продолжайте чтение.
Стремясь предоставить к ним практический подход, мы разработали реализацию javascript для каждого шифра, которая позволяет шифрование и дешифрование произвольного текста (по вашему выбору) с использованием этого шифра. Также включена история каждого шифра и даны советы по криптоанализу.
Какие эпохи криптографии?
Криптография прошла через множество этапов эволюции. Ранние шифры в криптографии были разработаны, чтобы обеспечить возможность шифрования и дешифрования вручную, в то время как те, которые разработаны и используются сегодня, возможны только благодаря высокой вычислительной производительности современных машин (то есть компьютера, который вы используете прямо сейчас).
Основные эпохи, сформировавшие криптографию, перечислены ниже.
Классический
Классические алгоритмы — это алгоритмы, изобретенные до компьютера примерно до 1950-х годов.Список ниже примерно упорядочен по сложности, наименее сложный вверху.
Механический
Механические шифры— это те, которые были разработаны во время Второй мировой войны и основаны на сложных механизмах передачи для шифрования текста.
Современное
Современные алгоритмы — это те, которые используются в современных технологиях, например. блочные шифры, криптосистемы с открытым ключом и т. д. Эти алогрифмы очень безопасны (в противном случае они не использовались бы), но во многих случаях мы можем практиковаться на ослабленных версиях алгоритмов.
Практическая криптография
В этом разделе описаны способы криптографического анализа и взлома многих криптографических шифров. Легче всего взломать шифры, которые существуют долгое время. Имея это в виду, мы сосредоточимся на классических шифрах, поскольку их легче всего объяснить.
На этой странице представлен очень общий обзор методов и приемов, используемых для криптоанализа практически любого алгоритма, шифрующего текст.Многое из этого будет немного математическим, но мы постараемся предоставить программы для всего. Это означает, что даже если вы не полностью понимаете теорию техники, вы все равно сможете ее использовать.
Большинство описанных здесь методов не работают с современными криптографическими алгоритмами, поэтому, если это то, что вы ищете, вы, вероятно, добьетесь большего успеха в поисках в другом месте.
Большая часть удовольствия от этих алгоритмов заключается в их взломе. Некоторые из более простых алгоритмов, такие как шифр Цезаря и шифр подстановки, могут быть решены вручную, в то время как другие, такие как ADFGVX и трехзначный шифр, легче решить с помощью компьютера.
Какие существуют методы?
Реализации шифров
В этот раздел будут включены реализации общих классических шифров на разных языках.
Конкретные примеры
Примеры в этом разделе описывают методы криптоанализа конкретных шифров. Эти примеры будут посвящены автоматизированным методам, то есть методам использования компьютера для взлома шифров.В целом эти методы будут отличаться от тех, которые используются для взлома шифров вручную.
Описание текста
При криптоанализе шифров мы обычно пробуем много «потенциальных» ключей, пока не будет найден ключ, который дает читаемый результат. Характеризация текста — это способ автоматического определения того, насколько фрагмент текста близок к естественному английскому языку, который может использоваться в качестве вспомогательного средства для криптоаналитика или в качестве компонента в программном обеспечении для автоматического взлома кода.
Шифры машины взлома
Этот раздел посвящен криптоанализу немного более продвинутых шифров, таких как Enigma и M-209, используемых во время Второй мировой войны. Они немного сложнее, чем простые примеры, приведенные в другом месте, однако они по-прежнему сильно зависят от разработанных методов, таких как восхождение на холм, с использованием индекса совпадения и статистики квадграмм.
Частота букв для разных языков
Предоставляет модели ngram для нескольких языков.
Современный криптоанализ
Этот раздел посвящен взлому современных шифров, представленные здесь методы не имеют много общего с классическими методами и в целом являются гораздо более математическими.
| 1 | Числовая последовательность | я | 4043 | 100 |
| 2 | Оригинальный шифр Цезаря | я | 2790 | 100 |
| 3 | Числовая последовательность — Часть 2 | я | 1973 | 100 |
| 4 | Цезарь Шифрование | я | 1330 | 100 |
| 5 | Бобр Код | я | 1097 | 100 |
| 6 | Письмо тамплиерам — Часть 1 | я | 961 | 100 |
| 7 | Числовая последовательность — Часть 3 | я | 926 | 100 |
| 8 | Письмо к тамплиерам. Часть 2 | я | 771 | 100 |
| 9 | Числовая последовательность — Часть 4 | я | 767 | 100 |
| 10 | Скрытое слово | я | 756 | 100 |
| 11 | Письмо к тамплиерам. Часть 3 | II | 656 | 1087 |
| 12 | Аффинные коды / Арифметика по модулю с N / Расширенный Евклид | я | 541 | 100 |
| 13 | Моноалфавитная замена | я | 523 | 100 |
| 14 | Взлом паролей с хешированием SHA1 | II | 494 | 1083 |
| 15 | Шифр факторизации — Часть 1 | я | 466 | 100 |
| 16 | Решетка Шифр | я | 446 | 100 |
| 17 | Advent-Challenge — Часть 1 | я | 385 | 100 |
| 18 | Модифицированный гомофонический шифр с сокращенными алфавитами — Часть 1 | я | 371 | 100 |
| 19 | Числовая последовательность — Часть 8 | я | 336 | 100 |
| 20 | Модифицированный гомофонический шифр с сокращенными алфавитами — Часть 2 | я | 318 | 100 |
| 21 | Подушечка одноразовая с изъянами | я | 293 | 100 |
| 22 | День рождения Алисы (часть 1) | II | 279 | 1082 |
| 23 | Белоснежка и семь гномов | я | 274 | 100 |
| 24 | День рождения Алисы (часть 2) | II | 272 | 1082 |
| 25 | Из России с любовью | я | 260 | 100 |
| 26 | Трансляция и низкий показатель степени — RSA Attack | II | 217 | 1084 |
| 27 | Модифицированный шифр Цезаря | я | 215 | 100 |
| 28 | Как стать крупным криптографом? | я | 209 | 100 |
| 29 | М-138 — Часть 1 | я | 191 | 100 |
| 30 | Не секретное сообщение из Малави — Часть I (ЮАР) | II | 183 | 1082 |
| 31 | Процедура резервной руки — Часть 1 | я | 182 | 100 |
| 32 | Атака грубой силой на Triple-DES с уменьшенным пространством ключей | II | 182 | 1082 |
| 33 | Письмо предполагаемой графини Джули фон Ортенбург | я | 166 | 100 |
| 34 | Классические шифры ^ 3 | я | 164 | 100 |
| 35 | Загадочные сообщения с повторяющимися буквами — Часть 1 | я | 160 | 100 |
| 36 | Гибридное шифрование I | II | 159 | 1082 |
| 37 | Нильс на выезде | я | 152 | 100 |
| 38 | RSA: два разных ключа — один и тот же зашифрованный текст | II | 150 | 1084 |
| 39 | Свинья с изюминкой — Часть 1 | я | 145 | 100 |
| 40 | Охота на кротов (Часть 1/3) | я | 141 | 100 |
| 41 | Шифр факторизации — Часть 2 | II | 139 | 1084 |
| 42 | Книжный код: вызов книжным червям | я | 137 | 100 |
| 43 | ¿Нет Hablas Español? Без проблем! | я | 137 | 100 |
| 44 | Охота на кротов (Часть 2/3) | я | 135 | 100 |
| 45 | Пазлы для взлома криптоанализа — Часть 2 | я | 134 | 100 |
| 46 | Шифр Autokey | я | 130 | 100 |
| 47 | Числовая последовательность — Часть 6 | я | 130 | 100 |
| 48 | Загадка, часть 1 | II | 127 | 1082 |
| 49 | М-138 — Часть 2 | II | 119 | 1094 |
| 50 | Секретное послание из замка Мансфельд | я | 118 | 100 |
| 51 | Трехзначный шифр | я | 114 | 100 |
| 52 | Шум изображения | я | 113 | 100 |
| 53 | Очень длинная числовая последовательность | II | 111 | 1084 |
| 54 | ADFGVX — Часть 2 | я | 111 | 100 |
| 55 | ADFGVX — Часть 1 | я | 103 | 100 |
| 56 | Шифрование Playfair | я | 103 | 100 |
| 57 | Playfair с подсказками о сетке | я | 102 | 100 |
| 58 | Каскаде-С / Т — Часть 1 | я | 101 | 100 |
| 59 | Двухстолбцовая транспозиция | я | 100 | 100 |
| 60 | Enigma Combinatorics | я | 96 | 100 |
| 61 | Числовая последовательность — Часть 10 | я | 95 | 100 |
| 62 | Постквантовая криптография: несбалансированная система масла и уксуса — Часть 1 | я | 94 | 100 |
| 63 | Скрытое слово — Часть 2 | я | 92 | 100 |
| 64 | Числовая последовательность — Часть 9 | я | 91 | 100 |
| 65 | Heartbleed — Часть 1 | я | 90 | 100 |
| 66 | Обмен ключами ECDH для начинающих | я | 89 | 100 |
| 67 | Шифр факторизации — Часть 3 | II | 88 | 1085 |
| 68 | Зодиакальный шифр | я | 86 | 100 |
| 69 | Загадка, часть 2 | II | 84 | 1082 |
| 70 | Числовая последовательность — Часть 5 | я | 82 | 100 |
| 71 | Hill Cipher с ключом судоку | я | 82 | 100 |
| 72 | Частичное раскрытие ключа с помощью RSA — часть 1 | II | 81 | 1085 |
| 73 | Потоковый шифр ORYX, часть I | II | 79 | 1082 |
| 74 | Последняя нота | я | 79 | 100 |
| 75 | Охота на кротов (Часть 3/3) | II | 78 | 1082 |
| 76 | Числовая последовательность — Часть 7 | я | 75 | 100 |
| 77 | Загадочные сообщения с повторяющимися буквами — Часть 3 | я | 73 | 100 |
| 78 | Загадочные сообщения с повторяющимися буквами — Часть 2 | я | 72 | 100 |
| 79 | Смарт-карта RSA | II | 71 | 1082 |
| 80 | Сообщения Enigma | я | 70 | 100 |
| 81 | Загадочные сообщения с повторяющимися буквами — Часть 5 | я | 70 | 100 |
| 82 | Многоязычная моноалфавитная замена | я | 69 | 100 |
| 83 | Код BCR (Книга-Цезарь-RSA) | II | 67 | 1086 |
| 84 | Каскадное шифрование — Часть 1/3 | я | 67 | 100 |
| 85 | Ключ AES — закодирован в машиночитаемой зоне европейского электронного паспорта | II | 66 | 1085 |
| 86 | Загадка бомбы Тьюринга I | я | 65 | 100 |
| 87 | Загадочные сообщения с повторяющимися буквами — Часть 4 | я | 64 | 100 |
| 88 | Одноразовый блокнот из вторсырья | я | 62 | 100 |
| 89 | Необычное шифрование с использованием диофантова уравнения | II | 61 | 1084 |
| 90 | Heartbleed — Часть 2 | я | 60 | 100 |
| 91 | Моноалфавитная замена с камуфляжем — Часть 1 | я | 59 | 100 |
| 92 | Модульные последовательности | я | 57 | 100 |
| 93 | Невидимое сообщение | я | 56 | 100 |
| 94 | М-138 — Часть 3 | II | 55 | 1094 |
| 95 | Загадка Эйнштейна | II | 52 | 1114 |
| 96 | Задача факторинга RSA: RSA-704 | II | 50 | 0 |
| 97 | Каскаде-С / Т — Часть 2 | II | 50 | 1083 |
| 98 | Незакрытые сообщения RSA | II | 48 | 1084 |
| 99 | Моноалфавитная замена с камуфляжем — Часть 2 | II | 48 | 1084 |
| 100 | Новости из замка Мансфельд | я | 48 | 100 |
| 101 | Потоковый шифр ORYX, часть II | II | 47 | 1082 |
| 102 | Моноалфавитная замена с камуфляжем — Часть 4 | я | 46 | 100 |
| 103 | Новогоднее поздравление — 1 часть | я | 45 | 100 |
| 104 | Keyshanc — Часть 1 | II | 45 | 1086 |
| 105 | Моноалфавитная замена с камуфляжем — Часть 3 | II | 44 | 1084 |
| 106 | Атака в обеденное время на схему полностью гомоморфного шифрования | II | 44 | 1082 |
| 107 | Проблема факторинга RSA: RSA-210 | II | 44 | 0 |
| 108 | Advent-Challenge — Часть 2 | II | 44 | 1113 |
| 109 | Летняя работа | II | 43 | 1118 |
| 110 | Странное послание из Салоников | я | 42 | 100 |
| 111 | Двойное транспонирование столбца — Часть 4 | II | 42 | 1092 |
| 112 | Новогоднее поздравление — часть 2 | я | 42 | 100 |
| 113 | Ослабленный гранит — Часть 1 | я | 42 | 100 |
| 114 | СЭВ 1 | II | 41 | 1082 |
| 115 | Музыкальный кодекс — часть 2 | II | 40 | 1083 |
| 116 | Новогоднее поздравление — часть 3 | я | 40 | 100 |
| 117 | «Невыносимое» сообщение | я | 40 | 100 |
| 118 | Музыкальный кодекс — часть 1 | я | 40 | 100 |
| 119 | Двойное транспонирование столбца — Часть 2 | II | 40 | 1092 |
| 120 | Новогоднее поздравление — часть 4 | я | 38 | 100 |
| 121 | Свинья с изюминкой — Часть 2 | II | 37 | 1084 |
| 122 | Ку-клукс-клан | Х | 36 | вар |
| 123 | Двойное транспонирование столбца — часть 3 | II | 36 | 1092 |
| 124 | Advent Challenge — Часть 3 | II | 36 | 1113 |
| 125 | Не секретное сообщение из Малави — Часть II (ECC) | II | 36 | 1082 |
| 126 | Advent Challenge — Часть 4 | II | 36 | 1113 |
| 127 | Найдите правильный маршрут — Часть 1 | я | 35 | 101 |
| 128 | Свинья с изюминкой — Часть 3 | II | 35 | 1084 |
| 129 | Keyshanc — Часть 2 | II | 35 | 1086 |
| 130 | Гомофоническое шифрование — Часть 1 | II | 32 | 1131 |
| 131 | Модный мессенджер | II | 31 | 1118 |
| 132 | Каскаде-С / Т — Часть 3 | II | 31 | 1083 |
| 133 | Облегченное введение в решетки — часть 1 | я | 31 | 100 |
| 134 | ORYX Stream Cipher — Часть 3 (пересмотренная) | II | 30 | 1089 |
| 135 | Самый быстрый на Западе | II | 30 | 1118 |
| 136 | Heartbleed — Часть 3 | II | 30 | 1093 |
| 137 | Проблема факторинга RSA: RSA-220 | II | 29 | 0 |
| 138 | Решетка, часть 1 | II | 28 | 1083 |
| 139 | Двойное транспонирование столбца — Часть 1 | II | 28 | 1091 |
| 140 | Моноалфавитная замена с камуфляжем — Часть 5 | II | 28 | 1085 |
| 141 | Испанский полосовой шифр — часть 1 | II | 28 | 1091 |
| 142 | СЭВ 2 | III | 27 | 13076 |
| 143 | Моноалфавитная замена вкусом Нострадамуса | II | 27 | 1127 |
| 144 | Полигомофоническая подмена — Часть 1 | я | 26 | 100 |
| 145 | Проблема факторинга RSA: RSA-230 | II | 26 | 0 |
| 146 | Пазлы для взлома криптоанализа — Часть 1 | я | 25 | 100 |
| 147 | Гомофоническое шифрование — Часть 2 | II | 25 | 1131 |
| 148 | Typex — Часть 1 | II | 25 | 1088 |
| 149 | Гомофоническое шифрование — Часть 3 | II | 24 | 1131 |
| 150 | Облегченное введение в решетки — часть 2 | я | 23 | 100 |
| 151 | RSA с Special d | III | 23 | 13071 |
| 152 | Гомофоническое шифрование — Часть 4 | II | 23 | 1131 |
| 153 | М-138 — Часть 4 | II | 22 | 1094 |
| 154 | Испанский полосовой шифр — часть 2 | II | 22 | 1091 |
| 155 | Typex — Часть 2 | II | 22 | 1088 |
| 156 | Handycipher made in love — Часть 1 | II | 21 | 1127 |
| 157 | Облегченное введение в решетки — часть 3 | II | 21 | 1175 |
| 158 | Разрушение фильтра-генератора | II | 18 | 1121 |
| 159 | Шифр полифонической замены — Часть 1 | II | 18 | 1145 |
| 160 | Фиолетовый 1 | II | 17 | 1082 |
| 161 | AES ECB Неверная кодировка | II | 17 | 1113 |
| 162 | Шифр LoRa: Логическая случайность — Часть 1 | II | 17 | 1153 |
| 163 | Полигомофоническая подмена — Часть 2 | II | 16 | 1158 |
| 164 | Handycipher made in love — Часть 2 | II | 16 | 1132 |
| 165 | Скрытые сообщения — Ночное небо Виженера | Х | 16 | вар |
| 166 | Ослабленный Handycipher — Часть 1 | II | 15 | 1096 |
| 167 | ASAC — Сильный (er) шифр ADFGVX — Часть 1 | II | 15 | 1102 |
| 168 | Шифр полифонической замены — Часть 2 | II | 15 | 1150 |
| 169 | Новогоднее поздравление — 5 часть | II | 15 | 1100 |
| 170 | Sigaba Часть 1 | II | 15 | 1082 |
| 171 | Скрытый шифр подстановки — часть 1 | II | 15 | 1138 |
| 172 | Идентификатор шифра — Часть 1 | II | 14 | 1144 |
| 173 | Скрытый шифр подстановки — часть 2 | II | 14 | 1138 |
| 174 | Проблема факторинга RSA: RSA-240 | III | 14 | 0 |
| 175 | Некорректное использование OTP шифра BND | II | 14 | 1097 |
| 176 | Ослабленный Handycipher — Часть 3 | II | 14 | 1096 |
| 177 | Ослабленный Handycipher — Часть 2 | II | 13 | 1096 |
| 178 | Каскадное шифрование — Часть 2/3 | II | 13 | 1088 |
| 179 | Найдите правильный маршрут — Часть 2 | я | 13 | 101 |
| 180 | Найдите правильный маршрут — Часть 3 | я | 13 | 101 |
| 181 | The T52 Sturgeon Challenge — Часть 1 | II | 13 | 1135 |
| 182 | Полигомофоническая подмена — Часть 3 | II | 12 | 1159 |
| 183 | RSA Factoring Challenge: RSA-250 | III | 12 | 0 |
| 184 | Каскадное шифрование — часть 3/3 | II | 12 | 1088 |
| 185 | The T52 Sturgeon Challenge — Часть 2 | II | 12 | 1136 |
| 186 | Потоковый шифр ORYX — Часть 4a | II | 11 | 1091 |
| 187 | Проблема факторинга RSA: RSA-232 | III | 11 | 0 |
| 188 | Постквантовая криптография: несбалансированная система масла и уксуса — Часть 2 | II | 11 | 1083 |
| 189 | Каскаде-С / Т — Часть 5 | II | 10 | 1083 |
| 190 | Акеларре Часть 1 | II | 10 | 1082 |
| 191 | The T52 Sturgeon Challenge — Часть 3 | II | 10 | 1136 |
| 192 | The T52 Sturgeon Challenge — Часть 4 | II | 9 | 1136 |
| 193 | Двойное транспонирование столбца — Часть 5 | II | 8 | 1092 |
| 194 | Вызов SZ42 — Часть 2 | II | 8 | 1180 |
| 195 | Вызов SZ42 — Часть 1 | II | 8 | 1177 |
| 196 | Холмы — Часть 1 | II | 8 | 1105 |
| 197 | Вызов SZ42 — Часть 4 | II | 7 | 1186 |
| 198 | Вызов SIGABA — Часть 1 | II | 7 | 1154 |
| 199 | Вызов SIGABA — Часть 2 | II | 7 | 1155 |
| 200 | Вызов SZ42 — Часть 3 | II | 7 | 1182 |
| 201 | Handycipher — Часть 2 | II | 7 | 1095 |
| 202 | The T52 Sturgeon Challenge — Часть 12 | II | 6 | 1137 |
| 203 | The T52 Sturgeon Challenge — Часть 8 | II | 6 | 1137 |
| 204 | The T52 Sturgeon Challenge — Часть 11 | II | 6 | 1137 |
| 205 | Голографическое шифрование — часть 1 | II | 6 | 1107 |
| 206 | Handycipher — часть 3 | III | 6 | 13299 |
| 207 | Вызов SZ42 — Часть 5 | II | 6 | 1187 |
| 208 | Каскаде-С / Т — Часть 6 (ВыкупKaskade Часть 1) | II | 6 | 1108 |
| 209 | Handycipher — Часть 6 | III | 5 | 13409 |
| 210 | «Дорога» — Часть 1 | II | 5 | 1124 |
| 211 | The T52 Sturgeon Challenge — Часть 10 | II | 5 | 1137 |
| 212 | The T52 Sturgeon Challenge — Часть 9 | II | 5 | 1137 |
| 213 | Ослабленный Handycipher — Часть 4 | II | 5 | 1102 |
| 214 | The T52 Sturgeon Challenge — Часть 7 | II | 5 | 1137 |
| 215 | Вызов SZ42 — Часть 6 | II | 5 | 1196 |
| 216 | Вызов SIGABA — Часть 3 | III | 5 | 14203 |
| 217 | Handycipher — Часть 5 | III | 5 | 13409 |
| 218 | Вызов SZ42 — Часть 8 | II | 5 | 1207 |
| 219 | Ослабленный Handycipher — Часть 6 | II | 5 | 1102 |
| 220 | Ослабленный Handycipher — Часть 5 | II | 5 | 1102 |
| 221 | Спираль — Часть 1 | II | 5 | 1097 |
| 222 | Handycipher — Часть 1 | II | 5 | 1095 |
| 223 | Спираль — Часть 2 | II | 5 | 1097 |
| 224 | Вызов SIGABA — Часть 4 | III | 4 | 14213 |
| 225 | The Heavy T52 Sturgeon Challenge — Часть 4 | III | 4 | 14262 |
| 226 | Спираль — Часть 3 | II | 4 | 1097 |
| 227 | Вызов SZ42 — Часть 7 | II | 4 | 1205 |
| 228 | Handycipher — Часть 4 | III | 4 | 13409 |
| 229 | Sigaba Часть 2 | III | 4 | 13071 |
| 230 | The T52 Sturgeon Challenge — Часть 6 | II | 4 | 1137 |
| 231 | Записки итальянского солдата | Х | 4 | вар |
| 232 | The T52 Sturgeon Challenge — Часть 5 | II | 4 | 1137 |
| 233 | Расширенный Handycipher — Часть 3 | II | 3 | 1095 |
| 234 | Дифференциальный криптоанализ — Часть 2 | II | 3 | 1151 |
| 235 | Расширенный Handycipher — Часть 1 | II | 3 | 1095 |
| 236 | Christmas Challenge 2019: Дифференциальный криптоанализ — Часть 1 | II | 3 | 1147 |
| 237 | Ватиканский вызов — часть 2 | Х | 3 | вар |
| 238 | Ватиканский вызов — Часть 1 | Х | 3 | вар |
| 239 | Ослабленная ElsieFour — Часть 1 | II | 3 | 1116 |
| 240 | Расширенный Handycipher — Часть 2 | II | 3 | 1095 |
| 241 | Ослабленная ElsieFour — Часть 3 | II | 3 | 1111 |
| 242 | Вызов SZ42 — Часть 9 | II | 3 | 1235 |
| 243 | Handycipher — Часть 8 | III | 3 | 13468 |
| 244 | Вызов SZ42 — Часть 10 | II | 3 | 1281 |
| 245 | Расширенный Handycipher — Часть 5 | III | 3 | 13409 |
| 246 | Расширенный Handycipher — Часть 4 | III | 3 | 13409 |
| 247 | Handycipher — Часть 9 | III | 3 | 13468 |
| 248 | The Heavy T52 Sturgeon Challenge — Часть 7 | III | 3 | 14276 |
| 249 | Голографическое шифрование — часть 2 | II | 3 | 1107 |
| 250 | ElsieFour — Часть 1 | III | 3 | 13555 |
| 251 | Вызов SZ42 — Часть 11 | II | 2 | 1281 |
| 252 | The Heavy T52 Sturgeon Challenge — Часть 3 | III | 2 | 14024 |
| 253 | Расширенный Handycipher — Часть 6 | III | 2 | 13409 |
| 254 | Потоковый шифр ORYX — Часть 4b | III | 2 | 13240 |
| 255 | Автор неизвестен | Х | 2 | вар |
| 256 | Вызов SIGABA — Часть 5 | III | 2 | 14228 |
| 257 | Handycipher — Часть 7 | III | 2 | 13468 |
| 258 | The Heavy T52 Sturgeon Challenge — Часть 5 | III | 2 | 14272 |
| 259 | Письмо Екатерины Арагонской королю Фердинанду, своему отцу (1509) | Х | 2 | вар |
| 260 | Двухстолбцовая транспозиция | Х | 2 | вар |
| 261 | Моноалфавитная замена с камуфляжем — часть 6 | II | 1 | 1086 |
| 262 | Подстановочный шифр с непрефиксными кодами | III | 1 | 13097 |
| 263 | Вызов SIGABA — Часть 6 | III | 1 | 14244 |
| 264 | The Heavy T52 Sturgeon Challenge — Part 9 | III | 1 | 14289 |
| 265 | The Heavy T52 Sturgeon Challenge — Part 6 | III | 1 | 14274 |
| 266 | Handycipher — Part 10 | II | 1 | 1134 |
| 267 | The Heavy T52 Sturgeon Challenge — Part 1 | III | 1 | 13997 |
| 268 | The Vatican Challenge — Part 4 | X | 1 | var |
| 269 | Hilly — Part 2 | II | 1 | 1111 |
| 270 | Beale Ciphers | X | 1 | var |
| 271 | ASAC — A Strong(er) ADFGVX Cipher — Part 2 | II | 1 | 1102 |
| 272 | Double-Column Transposition/Granit — Part 3 | II | 0 | 1096 |
| 273 | RSA Factoring Challenge: RSA-400 | III | 0 | 13125 |
| 274 | ASAC — A Strong(er) ADFGVX Cipher — Part 5 | II | 0 | 1102 |
| 275 | ASAC — A Strong(er) ADFGVX Cipher — Part 4 | II | 0 | 1102 |
| 276 | ASAC — A Strong(er) ADFGVX Cipher — Part 3 | II | 0 | 1102 |
| 277 | The Heavy T52 Sturgeon Challenge — Part 8 | III | 0 | 14278 |
| 278 | RSA Factoring Challenge: RSA-360 | III | 0 | 13125 |
| 279 | Double-Column Transposition/Granit — Part 2 | II | 0 | 1096 |
| 280 | RSA Factoring Challenge: RSA-380 | III | 0 | 13125 |
| 281 | Double-Column Transposition/Granit — Part 1 | II | 0 | 1096 |
| 282 | Kryptos | X | 0 | var |
| 283 | RSA Factoring Challenge: RSA-370 | III | 0 | 13125 |
| 284 | RSA Factoring Challenge: RSA-350 | III | 0 | 13125 |
| 285 | RSA Factoring Challenge: RSA-390 | III | 0 | 13125 |
| 286 | RSA Factoring Challenge: RSA-340 | III | 0 | 13125 |
| 287 | Spirale — Part 4 | III | 0 | 13335 |
| 288 | RSA Factoring Challenge: RSA-896 | III | 0 | 13125 |
| 289 | RSA Factoring Challenge: RSA-270 | III | 0 | 13125 |
| 290 | RSA Factoring Challenge: RSA-260 | III | 0 | 13125 |
| 291 | Weakened Granit — Part 3 | II | 0 | 1097 |
| 292 | Weakened Granit — Part 2 | II | 0 | 1097 |
| 293 | RSA Factoring Challenge: RSA-280 | III | 0 | 13125 |
| 294 | RSA Factoring Challenge: RSA-290 | III | 0 | 13125 |
| 295 | RSA Factoring Challenge: RSA-320 | III | 0 | 13125 |
| 296 | RSA Factoring Challenge: RSA-330 | III | 0 | 13125 |
| 297 | RSA Factoring Challenge: RSA-310 | III | 0 | 13125 |
| 298 | RSA Factoring Challenge: RSA-1024 | III | 0 | 13125 |
| 299 | RSA Factoring Challenge: RSA-300 | III | 0 | 13125 |
| 300 | RSA Factoring Challenge: RSA-309 | III | 0 | 13125 |
| 301 | RSA Factoring Challenge: RSA-410 | III | 0 | 13125 |
| 302 | RSA Factoring Challenge: RSA-420 | III | 0 | 13125 |
| 303 | «The Road» — Part 3 | II | 0 | 1124 |
| 304 | The Vatican Challenge — Part 5 | X | 0 | var |
| 305 | «The Road» — Part 2 | II | 0 | 1124 |
| 306 | Digital Signatures: DSA with Medium Fields | III | 0 | 13106 |
| 307 | RSA Factoring Challenge: RSA-2048 | III | 0 | 13125 |
| 308 | The third ENIGMA M4 message | X | 0 | var |
| 309 | D’Agapeyeff | X | 0 | var |
| 310 | The Vatican Challenge — Part 3 | X | 0 | var |
| 311 | ORYX Stream Cipher — Part 4d | III | 0 | 13194 |
| 312 | Double Column Transposition Reloaded — Part 1 | III | 0 | 13219 |
| 313 | Recovering the Private Key in the Fully Homomorphic Encryption Scheme | III | 0 | 13080 |
| 314 | Twelve-Year-Old Murder Case | X | 0 | var |
| 315 | Double Column Transposition Reloaded — Part 3 | III | 0 | 13219 |
| 316 | Kaskade-S/T — Part 4 | II | 0 | 1083 |
| 317 | RSA Factoring Challenge: RSA-617 | III | 0 | 13125 |
| 318 | RSA Factoring Challenge: RSA-500 | III | 0 | 13125 |
| 319 | World Record Challenge: Break 65 Bits of AES | III | 0 | 13071 |
| 320 | The Heavy T52 Sturgeon Challenge — Part 2 | III | 0 | 14006 |
| 321 | RSA Factoring Challenge: RSA-450 | III | 0 | 13125 |
| 322 | RSA Factoring Challenge: RSA-440 | III | 0 | 13125 |
| 323 | RSA Factoring Challenge: RSA-430 | III | 0 | 13125 |
| 324 | Weakened ElsieFour — Part 2 | II | 0 | 1116 |
| 325 | ORYX Stream Cipher — Part 4c | III | 0 | 13240 |
| 326 | RSA Factoring Challenge: RSA-460 | III | 0 | 13125 |
| 327 | RSA Factoring Challenge: RSA-480 | III | 0 | 13125 |
| 328 | RSA Factoring Challenge: RSA-490 | III | 0 | 13125 |
| 329 | Spanish Strip Cipher — Part 3 | X | 0 | var |
| 330 | Dorabella | X | 0 | var |
| 331 | RSA Factoring Challenge: RSA-1536 | III | 0 | 13125 |
| 332 | RSA Factoring Challenge: RSA-470 | III | 0 | 13125 |
| 333 | Double Column Transposition Reloaded — Part 2 | III | 0 | 13219 |
Welcome to pyca/cryptography — Cryptography 35.
0.0.dev1 документация криптография включает как высокоуровневые рецепты, так и низкоуровневые интерфейсы для
общие криптографические алгоритмы, такие как симметричные шифры, дайджесты сообщений и
ключевые производные функции. Например, чтобы что-то зашифровать с помощью криптография Рецепт симметричного шифрования высокого уровня :
>>> из cryptography.fernet import Fernet >>> # Положи это в безопасное место! >>> key = Fernet.generate_key () >>> f = Фернет (ключ) >>> токен = f.encrypt (b «Действительно секретное сообщение. Не для посторонних глаз.») >>> токен б '...' >>> f.decrypt (токен) б'А действительно секретное сообщение. Не для посторонних глаз.
Если вы хотите узнать больше о криптографии, мы рекомендовать Crypto 101 от Лоренса Ван Хаутвена и Cryptopals Crypto Проблемы.
Установка
Вы можете установить криптографию с pip :
$ pip установить криптографию
Дополнительные сведения см. В разделе «Установка».
Макет
Криптография в общих чертах разделена на два уровня. Один с сейфом
криптографические рецепты, которые практически не требуют выбора конфигурации. Эти
безопасны и просты в использовании и не требуют от разработчиков принятия множества решений.
Другой уровень — низкоуровневые криптографические примитивы. Это часто
опасны и могут быть использованы неправильно. Они требуют принятия решений и наличия
глубокое знание криптографических концепций в действии. Из-за
потенциальная опасность при работе на этом уровне, это называется
Слой «опасных материалов» или «хазмат».Они живут в cryptography.hazmat , и их документация всегда будет содержать
увещевание наверху.
Мы рекомендуем по возможности использовать слой рецептов и возвращаться к слой hazmat только при необходимости.
Слой опасных материалов
Проект криптографии с открытым исходным кодом
Примечание
криптография не подвергалась внешнему аудиту своего кода или
документация.
Если вы заинтересованы в обсуждении аудита, пожалуйста
связаться.
Как стать криптографом
Криптологи и криптоаналитики создают и расшифровывают коды, криптограммы и головоломки. Криптологи пишут шифры, алгоритмы и протоколы безопасности для шифрования данных, а криптоаналитики разбирают существующий код для расшифровки информации. Эти профессионалы обеспечивают безопасное общение и обмен информацией в правительстве, бизнесе и некоммерческих организациях.
По данным Бюро статистики труда (BLS), профессии, связанные с компьютерами и информационными технологиями, в период с 2018 по 2028 гг. Откроют около 546 200 новых рабочих мест.Поскольку киберугрозы и нарушения безопасности продолжают мешать финансовым учреждениям, правительственным учреждениям и бизнес-сектору, специалисты по криптологии остаются жизненно важными для обеспечения безопасности информации.
Чем занимается криптограф?
Криптографы защищают компьютерные системы и системы информационных технологий, создавая алгоритмы и шифры для шифрования данных. Они также часто выполняют обязанности криптоаналитика, расшифровывая алгоритмы и шифруя текст для расшифровки информации. Криптографы также анализируют существующие системы шифрования для выявления слабых мест и уязвимостей.Они разрабатывают и тестируют теории и методы криптологии, внедряя новые или модернизированные решения для шифрования. Работая с организациями и учреждениями, криптографы объединяют потребности безопасности с отраслевыми стандартами, обеспечивая надежную передачу данных.
Как криптоаналитики, профессионалы в области криптологии расшифровывают данные, разбирая алгоритмы и шифры для доступа к информации. Расшифровывая сообщения и кодируя системы, криптоаналитики лучше понимают, как избежать пробелов в безопасности.Эти профессионалы обладают знаниями и навыками в отраслях, требующих высокого уровня конфиденциальности. Шифрование и дешифрование данных позволяет криптографам и криптоаналитикам одинаково защищать людей, группы, предприятия и организации.
Криптографы работают на правительство, особенно для защиты военных данных и национальной безопасности. Они поддерживают целостность электронных медицинских записей и личной медицинской информации для медицинских компаний и организаций. Они также шифруют финансовые данные, такие как банковские записи, операции электронной коммерции, а также информацию о кредитных и дебетовых картах.
Рекламное объявление CyberDegrees.org — это сайт, поддерживаемый рекламой. Рекомендуемые или проверенные партнерские программы, а также все результаты поиска, поиска или соответствия школ предназначены для школ, которые нам компенсируют. Эта компенсация не влияет на рейтинг наших школ, справочники по ресурсам или другую независимую от редакции информацию, опубликованную на этом сайте.
Лучшие онлайн-программы
Изучите программы, которые вам интересны, с высокими стандартами качества и гибкостью, необходимыми для вывода вашей карьеры на новый уровень.
Шаги, чтобы стать криптографом
Путь к карьере в криптографии начинается со степени бакалавра в области информатики, компьютерной инженерии или смежных областях. Курсовая работа развивает базовые знания и навыки в области математики, компьютерных и информационных систем, а также языков программирования. Начинающим криптографам нужны сильные математические навыки. Они могут получить двойную специализацию, изучая математику наряду с компьютерной дисциплиной.Математика делает упор на структуры данных, абстрактную алгебру и алгоритмы, необходимые для карьеры в криптологии.
Для большинства вакансий в криптографии требуется не менее пяти лет опыта работы в области компьютерной безопасности и безопасности информационных технологий.
Позиции начального уровня в качестве программистов, аналитиков информационной безопасности или аналитиков компьютерных систем позволяют познакомиться с аппаратным и программным обеспечением безопасности информационных технологий. Роль среднего уровня в качестве менеджера по информационным технологиям или администратора сети и компьютерных систем также может дать будущим криптографам представление о дизайне информационных технологий, организации и лидерстве.
Многие работодатели предпочитают нанимать криптографов со степенью магистра или доктора. Программы магистратуры по кибербезопасности, математике или компьютерной инженерии приводят к позициям в криптографии. Нетехнические степени в области экономики, английского языка или государственного управления могут облегчить карьеру в этой области наряду с обширным опытом работы с компьютерами. Программы магистратуры также развивают исследовательские и аналитические навыки, применимые к криптографии.
Сертификаты по кибербезопасности предоставляют криптографам больше возможностей для карьерного роста и потенциального заработка.Сертификаты развивают навыки в этой области и демонстрируют опыт работодателям.
EC-Council предлагает программу сертифицированных специалистов по шифрованию (ECES) для обучения студентов и профессионалов алгоритмам, криптографии и стеганографии. Они участвуют в практическом применении шифров и алгоритмов, изучая концепции симметричной, ключевой и асимметричной криптографии.
Сертифицированные профессиональные данные по системам информационной безопасности от (ISC) ² расширяют знания о методах и принципах безопасности, отвечая требованиям к обучению в области кибербезопасности Министерства обороны США.
Основные навыки, необходимые для криптографа
Криптографам необходимы знания компьютерных систем, сети и архитектуры баз данных. Знание структур данных и алгоритмов остается важным, как и продвинутые математические навыки. Криптографы должны понимать сложную математическую теорию и применять концепции и методы к алгоритмам шифрования.
Специалисты по криптографии также владеют несколькими языками программирования. Обычно используемые языки включают Python, Java и C ++.
Благодаря пониманию программного и аппаратного обеспечения информационной безопасности, криптографы имеют представление о решениях безопасности. Опыт в поддержке информационных технологий улучшает эти навыки. Криптографы дополнительно имеют опыт работы с операционными системами, включая Microsoft Windows и UNIX.
Криптографы используют алгоритмы шифрования, основанные на симметричных и асимметричных шифрах с блоком ключей. Общие алгоритмы включают алгоритм тройного шифрования данных (Triple DES) и алгоритм Ривеста-Шамира-Адельмана (RAS).Triple DES защищает от вторжений в систему безопасности, применяя блочный шифр с симметричным ключом три раза к каждому набору данных. RAS была одной из первых широко используемых криптосистем с открытым ключом для передачи данных.
Путем анализа и критического мышления криптографы разрабатывают алгоритмы и шифры для защиты конфиденциальной информации. Они создают решения безопасности, выявляя, устраняя и смягчая существующие и будущие риски. Криптографы также интерпретируют зашифрованную информацию, расшифровывая ее, чтобы получить доступ к протоколам безопасности и защищенному контенту.
Криптографам необходимы сильные вербальные и невербальные коммуникативные навыки. Как люди, которым поручено шифрование и дешифрование данных, они часто работают в команде. Криптографы передают свои выводы коллегам, предоставляя подробные объяснения своих практик и процессов. Они также могут объяснять технические концепции нетехническим специалистам, делая сложные концепции и идеи доступными для широкой аудитории.
Заработная плата криптографа
При прогнозируемом росте занятости на 12% в период с 2018 по 2028 год профессии, связанные с компьютерными технологиями и информационными технологиями, будут значительно расти.Согласно PayScale, криптографы получают среднюю зарплату чуть более 73000 долларов.
Криптографы работают на государственные, технические и финансовые организации. Министерство обороны и Агентство национальной безопасности нанимают профессионалов в области криптографии для защиты систем и данных в военной сфере, национальной безопасности и кибербезопасности.
Компаниям, занимающимся информационными технологиями, таким как Microsoft, Amazon и Apple, нужны криптографы для защиты их данных наряду с данными их пользователей и потребителей.Банки, инвестиционные фирмы и бухгалтерские компании также полагаются на криптографов для защиты конфиденциальной финансовой информации.
Ищете другие программы для получения степени кибер-диплома?
Примечание : дополнительную информацию и советы можно найти в нашем Руководстве по сертификации кибербезопасности.
Узнайте, как стать криптографом
В 2020 году киберпространство заставит наш мир вращаться. Интернет используется подавляющим большинством нашего населения в той или иной форме, и этот новый мир нуждается в большой защите.Если вы заинтересованы в том, чтобы стать одним из шерифов кибер-мира, вам доступны несколько вариантов карьеры.
ОБЯЗАННОСТИ
Шифры, алгоритмы и системы безопасности вводятся в код криптографом. Как криптограф вы полностью контролируете эти коды и защищаете их от кибер-хакеров. Некоторые подробные конкретные обязанности могут включать:
- Гарантия: финансовые данные защищены и доступны только авторизованным владельцам счетов
- Создавайте системы безопасности, защищающие от любых рисков
- Убедитесь, что вся важная информация защищена от редактирования, копирования или удаления
- Анализируйте данные для решения любых проблем безопасности с помощью математические и / или статистические коды
- Проверить системы на наличие уязвимостей и убедиться в их точности и надежности
- Помощь в решении и решении проблем безопасности для правительства или бизнеса
- Будьте в курсе текущих исследований и стратегий кодирования и приложений
Криптография — это карьера с возможностью работать на правительство, ФБР, страховые агентства, университеты и многие другие.
Конкретные должностные обязанности будут меняться в зависимости от вашего работодателя. Криптограф, работающий на правительство, будет иметь другие ожидания, чем тот, который работает в крупном университете. ЧТО НУЖНО СТАТЬ КРИПТОГРАФОМ?
Важно завершить исследование не только должностных обязанностей криптографа, но и того, что требуется для получения этой важной должности. Обучение играет важную роль в требованиях. Маршрут получения технической степени — это то, что вам нужно изучить.Большинство работодателей ожидают по крайней мере степени бакалавра в области компьютерных наук, математики или компьютерной инженерии. Некоторые работодатели могут принимать нетехнические степени, однако будьте готовы подкрепить эту степень большим опытом работы.
Продолжение образования со степенью магистра наук или доктора только расширит ваше резюме и возможности трудоустройства.
ОПЫТ РАБОТЫ
Должность и работодатель, которых вы выберете, будут определять, какой опыт работы требуется.Некоторые должности могут потребовать пяти или более лет опыта работы с высшим образованием, в то время как другие могут занять три года или меньше на аналогичной должности. Например, если вы хотите подать заявку в Агентство национальной безопасности, будьте готовы к тому, что за вами будет большой опыт. Прежде чем подавать заявление о приеме на работу своей мечты, может потребоваться немного времени и поиск желаемого места работы, чтобы убедиться, что вы полностью подготовлены.
НАЦИОНАЛЬНОЕ АГЕНТСТВО БЕЗОПАСНОСТИ (NSA)
Агентство национальной безопасности — это базовый корабль безопасности и мира всего кода, шифрования, защиты и многого другого.Он защищает наше правительство и эту страну, помогая вооруженным силам и военным операциям. АНБ может быть отличным местом для поиска работы. Даже без технического образования вас могут рассмотреть для работы в АНБ. Они также проводят летние программы для студентов, желающих получить степень по математике или информатике.
ВАРИАНТЫ КАРЬЕРЫ
Если вы выбрали профессию криптографа и только что закончили учебу, то куда вы пойдете, чтобы сделать карьеру в этой области и что вы можете сделать? Некоторым посчастливилось занять должность сразу после получения степени.Некоторые роли, которые они могут взять на себя, включают следующие:
- Финансовый консультант
- Профессор университета
- Консультант по безопасности
Эти три варианта могут быть в верхней части списка карьеры криптографа. Декодер данных или сообщений или эксперт по шифрованию — вот некоторые должности, которые также могут заинтересовать потенциального криптографа.
КАКИЕ НАВЫКИ ВАЖНЫ В ДАННОЙ ПРОФЕССИИ?
Технические навыки — основа успешной карьеры криптографа.Требуется много подробных знаний и информации, особенно из-за высокого риска этой карьеры. Вам доверяют конфиденциальность чрезвычайно ценной информации, и когда вы станете этим доверенным экспертом, от вас будут ожидать, что вы будете придерживаться этой уверенности.
Hard Skills
- Базовое понимание основных языков программирования, например: C, C ++, Java и Python
- Сильные математические навыки; дискретная математика, линейная и / или матричная алгебра
- Базовое понимание теории сложности, теории информации и теории чисел
- Знания в области шифрования, цифровых подписей, обмена ключами
- Симметричная криптография: знание хэш-функций, кодов аутентификации сообщений и симметричное шифрование
- Специалист в области алгоритмов и структур данных
Теперь давайте оценим мягкие навыки, необходимые для того, чтобы стать криптографом.
Soft Skills
- Обладают здравым смыслом
- Умный
- Принятие новых вызовов
- Интерес к решению проблем и решению головоломок
- Надежный
- Критически мыслящий
Сертификация В настоящее время существует только один указанный сертификат, связанный с криптографией.