Симметричная криптография – Симметричное и асимметричное шифрование. Разбор алгоритма передачи шифрованных данных между серверами

Глава 4. Введение в криптографию. Симметричное шифрование

4.1. Основные понятия криптографии

До 70-х годов XX века криптографией называлась область науки и практической деятельности, связанная с изучением и разработкой методов шифрования данных. В настоящее время это область науки, техники и практической деятельности, связанная с разработкой, применением и анализом криптографических систем защиты информации.

Криптографическая система — это система обеспечения информационной безопасности сети или АИС, использующая криптографические средства. Может включать подсистемы шифрования, идентификации пользователей, электронной цифровой подписи и др.

Криптографические средства — методы и средства обеспечения информационной безопасности, использующие криптографические преобразования информации. В узком смысле под криптографическими средствами могут пониматься отдельные устройства, документы и программы, использующиеся для выполнения функций криптосистемы.

Криптографическое преобразование информации — преобразование информации с использованием одного из криптографических алгоритмов. К криптографическим алгоритмам относятся алгоритмы шифрования/дешифрования, хэширования, формирования и проверки электронной цифровой подписи, распределения ключей и множество других алгоритмов, каждый из которых предназначен для противодействия определенным угрозам информационной беопасности со стороны возможного нарушителя (противника, злоумышленника) или нежелательных воздействий естественного характера. Ьольшинство криптографических алгоритмов строятся на математической основе.

Криптография является частью боле общей науки — криптологии. Вторая часть криптологии — криптоанализ. До 70-х годов XX века эта наука занималась оценкой сильных и слабых стором методов шифрования, а также разработкой методов взлома шифров. В настоящее время криптоанализ — область науки, занимающаяся изучением криптографических систем защиты в поиске способов нарушения информационной безопасности, которую обеспечивает данная система. Таким образом, криптоанализ изучает методы прочтения зашифрованного текста без ключа, методы подделки электронной цифровой подписи (без знания закрытого ключа автора) и т.д. Криптография и криптоанализ

— две сильно взаимодействующие науки с противоположными целями. За последние несколько десятилетий они непрерывно и интенсивно развиваются, причем достижения одной из них заставляют другую быстро реагировать совершенствованием своего аппарата.

4.2. Шифрование

Шифрование — это процесс преобразования исходного сообщения M (называемого

открытым текстом) в форму M’ (зашифрованный текст или шифртекст). При этом провести обратное преобразование M’ в M возможно только обладая некоторой дополнительной информацией, называемой ключом.

Шифрование нередко путают с кодированием, но между двумя этими процессами есть значительная разница. Кодирование также представляет собой преобразование ис-

ходного сообщения в другую форму, но цель этого преобразования — удобство обработки или передачи сообщения. Например, символьный текст кодируется в двоичный (каждый символ заменяется последовательностью нулей и единиц) для того, чтобы его можно было хранить и обрабатывать в ЭВМ, а двоичный текст преобразовывается в последовательность электрических импульсов, для того, чтобы стала возможной его передача по кабелю. Цель шифрования — противоположная. Текст зашифровывается для того, чтобы посторонние лица, не обладающие ключом, не могли бы воспринять заложенную в нем информацию, даже располагая этим зашифрованным текстом. Таким образом, шифрование является средством обеспечения конфиденциальности информации.

Алгоритмы шифрования делятся на две большие группы:

1.Симметричное (традиционнное шифрование).

2.Шифрование с открытым ключом.

4.3.Симметричное шифрование

Всимметричных алгоритмах шифрования один и тот же ключ K используется для того, чтобы зашифровать сообщение и для его последующей расшифровки. Таким образом, и отправитель и получатель сообщения должны располагать одним и тем же ключом. Схематично это можно записать в виде:

M’ = E(M, K) M = D(M’, K),

где Е — функция шифрования (encrypt), а D — функция дешифрования (decrypt), обе используют ключ K в качестве одного из параметров.

Исторически симметричное шифрование появилось первым. Более того, до середины XX века это была единственная разновидность шифрования. Симметричные алгоритмы широко применяются и в настоящее время.

Далее мы рассмотрим ряд простых алгоритмов симметричного шифрования, на примере которых легко проанализировать такие их характеристики, как устойчивость к различным видам криптоанализа, а также некоторые базовые принципы криптографии. Затем будут рассмотрены алгоритмы, используемые в современных информационных системах.

Все алгоритмы симметричного шифрования можно разделить на три класса:

1.Подстановочные алгоритмы.

2.Перестановочные алгоритмы.

3.Алгоритмы, использующие и подстановку и перестановку (к этому классу относятся практически все современные алгоритмы, разработанные для защиты информации в ЭВМ).

4.4.Подстановочные алгоритмы

Подстановочные алгоритмы шифрования работают по следующему принципу: каж-

дый символ (или последовательность символов) исходного сообщения заменяются другим символом (или другой последовательностью символов).

Рассмотрим конкретные примеры.

1. Шифр Цезаря.

Самым древним и самым простым из известных подстановочных шифров является шифр, использовавшийся Юлием Цезарем. В этом шифре каждая буква исходного сообщения заменяется буквой, находящейся в алфавите на три позиции после нее.

Рис. 1. Пример шифрования по Цезарю

Особенностью шифра Цезаря, как несложно заметить, является отсутствие ключа. Часло 3 в данном случае ключом не является, поскольку не выбирается отправителем сообщения, а используется для сдвига по алфавиту постоянно. Во времена Юлия Цезаря это не было слабостью шифра (поскольку сама идея сокрытия информации путем преобразования текста была незнакомой его противникам), но в настоящее время первым правилом криптографии является следующее допущение:

Стойкость любого шифра определяется в предположении, что противнику полностью известен механизм шифрования и единственной информацией, которой он не располагает, является ключ.

Данное допущение особенно актуально для настоящего времени, когда сложность шифров достигла такого уровня, что зашифровывать и расшифровывать сообщения вручную просто невозможно. Для этих целей используется программное обеспечение, которое заинтересованные лица могут детально проанализировать и, таким образом, полностью восстановить алгоритм шифрования.

Это правило имеет тенденцию нарушаться в тех областях, когда криптографиечское программное обеспечение не предназначено для широкого распространения. Например, алгоритмы, использующиеся в системах электронного голосования, правительственной связи и др. Разработчики этих систем считают сокрытие алгоритмов шифрования фактором, усиливающим безопасность. Однако считается научно установленной ошибочность этого предположения. Злоумышленник, серьено заинтересованный в том, чтобы взломать криптографическую защиту и нарушить конфиденциальность данных, почти наверняка найдет способ получить доступ к самой программе, которая по определению не может быть также хорошо защищена, как обрабатываемые ею данные, и изучить используемые алгоритмы. Сокрытие алгоритмов и деталей архитектуры таких систем лишь препятствует их изучению независимыми исследователями и увеличивает опасность того, что алгоритмы, положенные в их основу, будут недостаточно надежными3.

3 Так, например, в 2007 году в результате утечки информации оказались обнародованы алгоритмы, используемые в популярной технологии KeeLoq — системы охраны, применяемой в противоугонных средствах автомобильной защиты. После исследования, проведенного независимыми экспертами, оказалось, что при сравнительно скромных затратах времени и вычислительных ресурсов (два дня работы компьютеров общей ценой около 10 000 евро) злоумышленники могут вскрыть сначала секретный ключ какой-либо конкретной машины, а на его основе — но теперь уже за секунды — цифровой ключ любого другого автомобиля этой же компании. Двумя годами раньше аналогичный скандал возник с системой электронного голосования, использовавшейся в США, исходные коды которой оказались случайно выложенными в общий доступ на сайте компании. Исследование показало уязвимость системы к целому спектру популярных атак.

Рассмотрим вариацию шифра Цезаря, при которой число 3 является не жестко заданным, а выбирается произвольно, согласно договоренности между отправителем и получателем сообщения. В этом случае шифр Цезаря становится полноценным шифром с ключом K (потенциально неизвестном противнику).

Однако легко заметить, что в качестве ключа могут быть выбраны лишь числа в диапазоне от 1 до 32 (для русского алфавита). Действительно, шифр является циклическим: Я + 1 = А, но и Я + 34 = А. То есть, число 34, выбранное в качестве ключа, будет эквивалентно ключу 1, ключ 35 — ключу 2 и т.д. Противнику ничего не стоит перебрать все 32 возможных ключа и обнаружить нужный4.

Таким образом, модифицированный шифр Цезаря является неустойчивым ко взлому методом перебора возможных ключей по причине их малого диапазона или, как говорят,

малой длины ключа.

2. Моноалфавитный шифр (шифр простой замены)

Один из хорошо известных подстановочных шифров. Каждому символу алфавита открытого текста ставится в соответствие некоторый символ другого алфавита. Он может и совпадать с первым (тогда одна буква заменяется другую). При шифровании каждая символ открытого текста заменяется на соответствующий ему другой символ.

Ключом к данному шифру будет являться таблица соответствий, которую удобно представить в виде символов, выписанных в алфавитном порядке тех букв, которые они заменяют. Другими словами, ключом является перестановка символов алфавита зашифрованного текста.

Рис. 2. Пример шифрования текста шифром простой замены

В данном случае число возможных ключей равно числу возможных перестановок из 33 букв, то есть, 33!. Даже при использовании миллиона компьютеров, проверяющих миллион возможных ключей в секунду, перебор всех вариантов займет больше миллиона лет. Таким образом, моноалфавитный шифр является стойким ко взлому методом перебора возможных ключей.

Однако данный шифр достаточно просто поддается криптоанализу, который начинается с подсчета каждого символа шифртекста и определения частоты его встречаемости.

4 При этом необязательно даже расшифровывать весь текст сообщения: после опробования ключа на первом же десятке символов станет понятно, получаем ли мы бессмысленный набор символов (следовательно, ключ не подходит), или что-то, похожее на настоящий текст.

Для достаточно длинного сообщения (порядка 4—5 предложений) этой информации будет достаточно, чтобы сопоставить ее с таблицей частоты встречамости букв языка.

Все естественные языки имеют характерное частотное распределение символов. Например, буква «О» — встречается в русском языке чаще других, а буква «Ф» — самая редкая (см. табл. 1).

	Табл. 1. Таблица частот встречаемости букв русского языка.
Символ	Вероятность	Символ	Вероятность	Символ	Вероятность
пробел	0.175	К	0.028	Ч	0.012
О	0.089	М	0.026	Й	0.010
Е	0.072	Д	0.025	Х	0.009
А	0.062	П	0.023	Ж	0.007
И	0.062	У	0.021	Ю	0.006
Н	0.053	Я	0.018	Ш	0.006
Т	0.053	Ы	0.016	Ц	0.004
С	0.045	З	0.016	Щ	0.003
Р	0.040	Ь	0.014	Э	0.003
В	0.038	Б	0.014	Ф	0.002
Л	0.03	Г	0.013

На основе частоты встречаемости символов зашифрованного текста можно сделать предположения о некоторых, наиболее часто встречающихся из них, а затем, опираясь на эти предположения, постепенно восстанавливать слова текста, начиная с самых коротких

— предлогов и союзов. Так, в английском языке достаточно легко идентифицируется артикль the — самая часто встречающаяся комбинация из трех букв.

Таким образом, моноалфавитные шифры имеют серьезную слабость к криптоанали-

зу на основе статистических особенностей исходного текста, которые наследует за-

шифрованный текст. Противнику даже не нужно целенаправленно подбирать ключ — он сам восстанавливается по ходу дела.

Нетрудно заметить, что шифр Цезаря также является моноалфавитным шифром.

3. Шифр Гронсфельда

Рассмотрим шифр, предсталяющий собой модификацию шифра Цезаря. В качестве ключа используется последовательность цифр произвольной фиксированной длины. Каждая цифра этой последовательности записывается под одним символом открытого текста, причем если длина ключа меньше длины текста, ключ циклически повторяется. Зашифруем слово «информатика» ключом «123».

Рис. 3. Пример шифрования текста шифром Гронсфельда

Данный шифр (описанный Жюль Верном в романе «Жангада») относится к семейст-

ву многоалфавитных шифров (или шифров сложной замены). В многоалфавитном шифре

1-й символ открытого текста шифруется с помощью моноалфавитного шифра, ключом к которому является перестановка K1, 2-й символ — ключом K2 и т.д., n-й символ — ключом Kn, а n+1-й — снова ключом K1, где n — количество используемых алфивитов (или шифров простой замены). В приведенном примере n=3.

Особенности многоалфавитных шифров хорошо демонстрирует шифр Гронсфельда (и, в частности, приведенный пример). Мы видим, что одна и та же буква «и» превращается то в «й», то в «л» в зависимости от того, какая цифра ключа использовалась для шифрования, а буква «а» может быть зашифрована как «б» или «в». Более того, буква «п», встречающаяся в зашифрованном тексте три раза, каждый раз означает разные буквы.

Таким образом, хотя статистические особенности исходного текста и будут проявляться с цикличностью n, где n — длина ключа, при достаточно большом n (десять и более цифр, при том, что противнику эта длина неизвестна), таблицы частот дают гораздо большую погрешность, не говоря уже о том, что проверять предположения, восстанавливая фрагменты по смыслу, становится практически невозможным.

Главная слабость шифра Гронсфельда в том, что каждая буква зашифрованного текста отстоит от «своей» буквы открытого текста не более, чем на девять позиций в алфавите, а это дает противику возможность легко проверять различные предположения. Например, предположив, что начало зашифрованного текста «йпчптпбфллв» расшифровывается как «крипто», уже на первом символе, противник отбросит этот вариант, поскольку буква «к» не может превратиться в «й» после сдвига.

Эта проблема исчезает в модификации шифра Гронфельда, где в качестве ключа выступает не цифровая, а буквенная последовательность. Порядковый номер буквы открытого текста складывается с записанной под ней буквой ключа и получается порядковый номер буквы зашифрованного текста (который берется по модулю мощности алфавита,

т.е. Г + Э = 4 + 31 = 35; 35 mod 33 = 2 = Б; Г + Э = Б).

Рис. 4. Модифицированный шифр Гронсфельда

Механизм «сложения» исходного текста с ключом, представляющим собой цифровую или буквенную поседовательность, который мы наблюдали в шифрах Цезаря и Гронсфельда, используется и во многих других шифрах. Особенностью таких шифров яв-

ляется возможность восстановления ключа, если известны открытые и зашифрованный текст. Это делается операцией, обратной «сложению» — «вычитанием»5.

Таким образом, если противник располагает открытым текстом и соответствующим ему зашифрованным текстом, он может получить ключ и попробовать применить его к другим зашифрованным текстам (поскольку нередко один ключ используется для многих сообщений). Этот метод называется криптоанализом с известным открытым текстом и,

очевидно, шифр Гронсфельда легко ему поддается.

Для того, чтобы получить пару «открытый текст — зашифрованный текст» противник может вынудить отправителя сообщения зашифровать определенную информацию (например, в истории разведки не раз применялся прием, когда с этой целью нарочно организовывалась утечка информации). Кроме того, противник может делать предположения о словах, которые могут встречаться в тексте исходного сообщения (особенно продуктивны попытки угадать первое слово), и, пробуя эти слова, вычислять фрагменты возможного ключа. Далее эти фрагменты пробуются в других участках зашифрованного текста и, если в результате обратного преобразования получается осмысленная последовательность, криптоаналитик на верном пути.

4. Многобуквенные шифры

В определении подстановочных шифров сказано, что при шифровании может заменяться не каждый отдельный символ исходного сообщения, а сразу группа символов — на другую группу символов. Такие шифры называются многобуквенными. Рассмотрим шифр Плейфейера, в котором единицей шифрования является биграмма (пара букв), заменяемая другой парой букв.

Шифр предназначен для английского алфавита. Ключом является кодовая фраза, которая записывается в первые ячейки квадратной решетки 5×5 (повторяющиеся буквы пропускаются). Затем квадрат в алфавитном порядке заполняется буквами, которые не вошли в кодовую фразу. I и J считаются одной буквой.

Заполним решетку с ключевым словом MONARCHY.

Рис. 5. Кодовая решетка для шифра Плейфейера

Исходный текст разбивается на биграммы. При этом если две одинаковые буквы открытого текста при разбиении образуют одну биграмму, между ними вставляется символ

X. Т.е. вместо BALLOON шифруем BALXLOON.

5 При вычитании одного текста из другого отсчет идет по алфавиту назад. Если получилось отрицательное число, к нему прибавляется мощность (число букв) алфавита. Математически происходит вычитание порядковых номеров букв по модулю мощности алфавита.

Если буквы биграммы стоят в одной строке (столбце), они заменяются их правыми (нижними) соседями с учетом циклического сдвига. В нашем примере OR шифруется как

NM, а OP — как HV.

Если буквы биграммы оказываются в разных строках и столбцах, то каждая из пары букв заменяется буквой, находящейся на пересечении ее строки и столбца, в котором находится вторая буква. Например, BE шифруется как CI, а OS — как AP.

Слово INFORMATION будет зашифровано как GAPHMORSFAAW.

Данный шифр сохраняет статистические особенности исходного текста в том смысле, что можно построить таблицу частот биграмм для языка и проанализировать частоты биграмм зашифрованного текста. Однако если букв в английском языке 26, то биграмм уже 262 = 676, поэтому задача существенно усложняется и без весьма значительных объемов зашифрованного текста обречена на провал.

Другой интересный пример многобуквенного шифра — шифр Хилла. Он представляет собой систему из m линейных уравнений с m коэффициентами. Шифр заменяет каждые m букв открытого текста на m букв зашифрованного текста. Например, при m = 3 имеем систему уравнений (где n — мощность алфавита):

c1 = (k11 p1+ k12 p2+ k13 p3) mod n c2 = (k21 p1+ k22 p2+ k23 p3) mod n c3 = (k31 p1+ k32 p2+ k33 p3) mod n

Ключом шифрования будет являться матрица коэффициентов K, а само шифрование можно представить как произведение вектора, составленного из порядковых номеров букв открытого текста (первая буква имеет номер 0) на ключевую матрицу K:

c3 k 31k					32 k		33 p3
c1		k	11k		12 k		13	p1
c	2	= k	21	k	22	k	23	p	2

Для расшифровки зашифрованный текст необходимо умножить на матрицу, обрат-

ную к K (K-1).

Шифр Хилла также хорошо скрывает частоту символов исходного сообщения, но уязвим к криптоанализу с известным открытым текстом. Поскольку система линейная, противнику понадобится m2 пар «открытый текст — зашифрованный текст», чтобы вычислить ключевую матрицу. Однако наиболее эффективный метод криптоанализа для данного шифра — криптоанализ с избранным открытым текстом, когда противник имеет возможность получать зашифрованные образцы специально подобранного им открытого текста6. Посмотрите, что будет представлять из себя зашифрованный текст, если зашифровать последовательность БАА ( p1 = 1, p2 = 0, p3 = 0).

5. Одноразовый блокнот

6 Например, имеется система передачи данных по каналу связи в зашифрованном виде, которая использует один и тот же ключ для шифрования всех данных. При этом противник может перехватывать передающиеся по каналу связи зашифрованные сообщения, а также передавать свои собственные. В этом случае он может получить интересующие его пары «открытый текст — зашифрованный текст» и с их помощью провести криптоанализ ключа.

studfiles.net

Симметричная криптография. Основные понятия

Рассмотрим общую схему симметричной, или традиционной, криптографии.

Рис. 1. Общая схема симметричного шифрования

В процессе шифрования используется определенный алгоритм шифрования, на вход которому подаются исходное незашифрованное сообщение (называемое plaintext), и ключ.

Выходом алгоритма является зашифрованное сообщение, (называемое ciphertext) .

Ключ является значением, не зависящим от шифруемого сообщения.

Изменение ключа должно приводить к изменению зашифрованного сообщения.

Зашифрованное сообщение передается получателю. Получатель преобразует зашифрованное сообщение в исходное незашифрованное

сообщение с помощью алгоритма дешифрования и того же самого ключа, который использовался при шифровании, или ключа, легко получаемого из ключа шифрования.

Незашифрованное сообщение будем обозначать P или M, от слов plaintext и message. Зашифрованное сообщение будем обозначать С, от слова ciphertext.

Безопасность, обеспечиваемая традиционной криптографией, зависит от нескольких факторов:

1) Во-первых, криптографический алгоритм должен быть достаточно сильным, чтобы передаваемое зашифрованное сообщение невозможно было расшифровать без ключа, используя только различные статистические закономерности зашифрованного сообщения или какие-либо другие способы его анализа.

2) Во-вторых, безопасность передаваемого сообщения должна зависеть от секретности ключа, но не от секретности алгоритма.

Алгоритм должен быть проанализирован специалистами, чтобы исключить наличие слабых мест, при наличии которых плохо скрыта взаимосвязь между незашифрованным и зашифрованным сообщениями. К тому же при выполнении этого условия производители могут создавать дешевые аппаратные чипы и свободно распространяемые программы, реализующие данный алгоритм шифрования.

3) В-третьих, алгоритм должен быть таким, чтобы нельзя было узнать ключ, даже зная достаточно много пар (зашифрованное сообщение, незашифрованное сообщение), полученных при шифровании с использованием данного ключа.

Клод Шеннон ввел понятия диффузия и конфузия для описания стойкости алгоритма шифрования.

Диффузия — это рассеяние статистических особенностей незашифрованного текста в широком диапазоне статистических особенностей зашифрованного текста.

Это достигается тем, что значение каждого элемента незашифрованного текста влияет на значения многих элементов зашифрованного текста или, что то же самое, любой элемент зашифрованного текста зависит от многих элементов незашифрованного текста.

Конфузия — это уничтожение статистической взаимосвязи между зашифрованным текстом и ключом.

Если: Х — это исходное сообщение и K — криптографический ключ, то зашифрованный передаваемый текст можно записать в виде

Y = E_K[X].

Получатель, используя тот же ключ, расшифровывает сообщение

X = D_K[Y]

Противник, не имея доступа к K и Х, должен попытаться узнать Х, K или и то, и другое.

Алгоритмы симметричного шифрования различаются способом, которым обрабатывается исходный текст.

Возможно шифрование:

— блоками

— потоком.

Блок текста рассматривается как неотрицательное целое число, либо как несколько независимых неотрицательных целых чисел.

Длина блока всегда выбирается равной степени двойки.

В большинстве блочных алгоритмов симметричного шифрования используются следующие типы операций:

• Табличная подстановка, при которой группа бит отображается в другую группу бит. Это так называемые S-box .

• Перемещение, с помощью которого биты сообщения переупорядочиваются.

• Операция сложения по модулю 2, обозначаемая XOR или

• Операция сложения по модулю 2³² или по модулю 2¹⁶.

• Циклический сдвиг на некоторое число бит.

Эти операции циклически повторяются в алгоритме, образуя так называемые раунды.

Входом каждого раунда является выход предыдущего раунда и ключ, который получен по определенному алгоритму из ключа шифрования K.

Ключ раунда называется подключом .

Каждый алгоритм шифрования может быть представлен следующим образом:

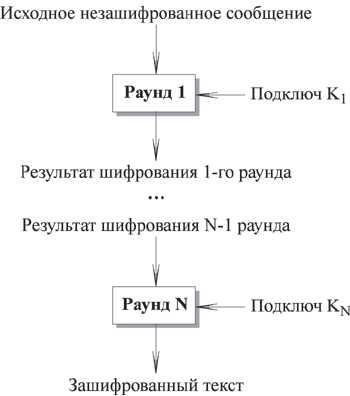
Рис. 2. Структура алгоритма симметричного шифрования

studfiles.net

Симметричное и асимметричное шифрование: определение понятия, применение, примеры

Чтобы обмениваться посланиями и скрыть содержание от третьих лиц, применяют шифрование. Оно используется там, где необходим повышенный уровень защиты. Есть две схемы шифрования: симметричная и асимметричная.

Что такое шифрование

Шифрование будет полезно тогда, когда нужно скрыть некоторую информацию от посторонних лиц и предоставить секретные данные авторизованным пользователям.

Особенностью такого вида передачи данных является использование ключа.

Есть три состояния безопасности:

• скрытие информации от посторонних;
• предотвращение изменений;
• сохранение целостности информации;
• идентификация отправителя.

Для чтения информации, кроме ключа, требуется дешифратор. Именно это обеспечивает невозможность получения данных злоумышленниками, ведь перехватив данные, но не имея ключа, прочесть их невозможно.

Бывают два вида шифрования: симметричный и асимметричный.

Главной целью шифрования является хранение информации. Это позволяет работать с некоторыми данными из ненадежных источников, передавать сообщения по незащищенным каналам. Отправка информации происходит так:

• отправитель шифрует данные;
• получатель расшифровывает.

Каждое преобразование реализуется с помощью алгоритмов, для решения которых используются ключи. Симметричные и асимметричные методы шифрования отличаются криптостойкостью.

Криптостойкость

Симметричные и асимметричные системы шифрования имеют такую характеристику, которая отвечает за сложность получения несанкционированного доступа.

Существует 2 основных типа криптостойкости системы шифрования.

1. Абсолютно стойкая система не может быть раскрыта, даже при наличии бесконечно больших вычислительных ресурсов. Характеризуется тем, что для каждого сообщения генерируется свой отдельный ключ. Его длина равна или больше длины сообщения.
2. Достаточно стойкие системы применяются в криптографической системе гражданского назначения. Такой алгоритм сложно расшифровать, но при наличии соответствующих ресурсов это становится возможным.

Сравнение криптостойкости некоторых систем шифрования

Максимальный размер ключа RSA — 4096 бит.

Он используется для шифрования и подписи. Криптостойкость можно описать как 2,7•1028 для ключа 1300 Бит. Схема применяется во многих стандартах, принцип шифрования RSA один из первых асимметричных алгоритмов.

Размер ключа схемы Эль-Гамаля равен RSA — 4096 Бит. Он используется и для шифрования, и для цифровой подписи. Криптостойкость этой системы не отличается от RSA при одинаковом размере ключа.

В методе DSA используется значительно меньшей ключ — 1024 бита. Применяется он исключительно для цифровой подписи.

Симметричное и асимметричное шифрование

Эти два вида шифрования отличаются количеством ключей и уровнем устойчивости к взлому.

Если для кодирования и раскодирования используется один ключ, то это шифрование симметричное. Асимметричное шифрование подразумевает использование одного ключа для каждого алгоритма.

1. Открытым ключом шифруется некоторый код, который представляет собой определенное послание. Ключ известен обеим сторонам, он передается по незащищенному каналу, может быть перехвачен. Важнейшей задачей сохранения информации является защита ключа от перехвата.
2. Закрытый используется для расшифровывания. Известен только одной стороне. Не может быть перехвачен, так как все время находится у одного собеседника.

Цель шифрования определяет метод сохранения конфиденциальности. Одним из первых было симметричное, асиметричное шифрование изобретено позже для обеспечения большей надежности.

Особенности симметричного шифрования

Симметричная система защита имеет следующие достоинства.

1. Высокая скорость и простота реализации.
2. Для обеспечения стойкости шифра используется малая длина ключа.

К недостаткам относится следующее:

• сложность управления ключами в большой сети;
• сложность обмена ключами;
• потребность в поиске надежного канала для передачи ключа сторонам;
• невозможность использования для цифровой подписи, сертификатов.

Для компенсации недостатков используется комбинированная схема, в которой с помощью асимметричного шифрования передается ключ, используемый для дешифровки. Он передается при помощи симметричного шифрования.

Особенности асимметричного шифрования

Применение пары открытый-закрытый ключ можно использовать как:

• самостоятельное средство защиты информации;
• средство распределения ключей;
• средства аутентификации пользователей.

Имеет такие преимущества:

• сохранение секретного ключа в надежном месте, вместо которого по открытому каналу передается открытый;
• ключ дешифрования известен только одной стороне;
• в большой асимметричной системе используйте меньшее количество ключей в отличие от симметричной.

В таких алгоритмах сложно внести какие-либо изменения. Подобная система имеет длинные ключи. Если симметричный ключ имеет размер 128 Бит, то ключ RSA — 2304 Бит. Из-за этого страдает скорость расшифровывания — она в 2-3 раза медленнее. Для расшифровки требуются большие вычислительные ресурсы.

Существует очень много примеров симметричной и асимметричной систем шифрования.

Симметричное шифрование — как выглядит?

Пример симметричного шифрования и схема реализации ниже.

1. Есть два собеседника, которые планируют обменяться конфиденциальной информацией.
2. Первый собеседник генерирует ключ d, алгоритмы шифрования E и дешифрования D. Затем посылает эту информацию второму собеседнику.
3. Сообщение дешифруется ключом d.

Главным недостатком является невозможность установить подлинность текста. В случае перехвата ключа злоумышленник расшифрует секретную информацию.

Существуют классические методы.

1. Простая и двойная перестановка.
2. Магический квадрат.
3. Одиночная перестановка.

Первый метод является одним из простейших, в схеме которого не используется ключ. Отправитель и получатель договариваются о некотором ключе, представленным в виде размера таблицы. Передаваемое сообщение записывается в столбцы таблицы, но считывается по строкам. Зная размер таблицы, получатель расшифровывает сообщение.

Для обеспечения большей скрытности используется двойная перестановка. Таким образом происходит шифрование ранее зашифрованного текста. Для этого таблицы должны отличаться количеством строк и столбцов. Они заполняются вертикально, горизонтально, змейкой, по спирали. Этот способ не усиливает шифрование, но процесс взлома становится более длительным.

“Магический квадрат” — более сложная структура, которая представляет собой матрицу. В клетки вписываются натуральные числа таким образом, чтобы сумма чисел по каждому столбцу, строке, диагонали была одинаковой. Каждое число соответствует букве сообщения. Полученный текст выписывается в строку, сопоставляя числа и символы.

Примеры асимметричного шифрования

В данном случае открытый ключ отправляется по открытому каналу и теоретически может быть перехвачен злоумышленниками.

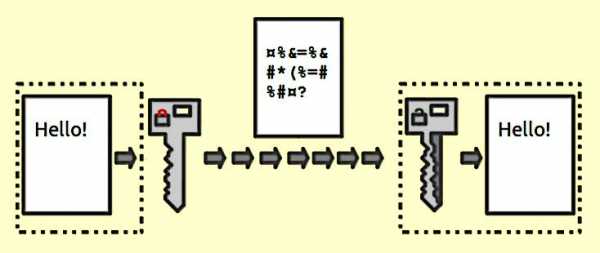
В отличие от симметричных, асимметричные ключи шифрования разные. Для шифровки применяется открытый ключ, для расшифровки послания — закрытый. Использование двух ключей решает проблему возможности перехвата, которая была в симметричном методе. Реализуется так.

1. Первый собеседник выбирает алгоритмы шифрования и дешифрования, пару ключей. Открытый ключ посылает второму собеседнику.
2. Второй собеседник шифрует информацию с помощью полученного ключа. Отправляет информацию первому собеседнику, который расшифровывает сообщение с помощью закрытого ключа.

Существует такие основные методы асинхронного шифрования.

1. RSA.
2. DSA.
3. Шифр Эль-Гамаля.

RSA

RSA — первый криптографический алгоритм, используемый и для шифрования, и для цифровой подписи.

Описывается так.

1. Выбирается два простых числа, например, 3 и 7.
2. Вычисляется модуль n — произведение двух чисел. Получается 21.
3. Вычисляется функция Эйлера φ=(p-1)×(q-1)=2×6=12.
4. Вычисляется любое простое число e меньше φ и простое с φ. Доступные варианты: 5, 7, 11.

Пара чисел e, n (5, 21) — открытый ключ. Теперь вычисляются числа d и n закрытого ключа. Число d удовлетворяет условие (d×е) mod φ=1 и равняется 17. В итоге вторая пара чисел 17 и 21 — закрытый ключ. Шифрование выполняется следующим образом: сообщение возводится в степень e, берется остаток от деления на n, при этом результат должен быть меньше числа n. Получается 10 — это будут закодированные данные. Для раскодировки e возводится в степень d, вычисляется остаток от деления на n.

DSA

DSA (в отличие от RSA) используется только для цифровой подписи, но не для шифрования. Заданная подпись может быть проверена публично. Есть два алгоритма для создания подписи и проверки. Шифруется именно хеш-сообщение, которое представляет текст в цифровом виде. Поэтому для избежания коллизий выбирается сложная хэш-функция. Построение цифровой подписи состоит из следующих шагов.

1. Выбор криптографической хэш-функции H(x).
2. Битность простого числа q должна равняться значению хэш-функции H(x).
3. Подбор такого простого числа p, чтобы p-1 делился без остатка на q.
4. Вычисление числа g = h (p-1)/q mod p. h должно быть произвольным числом в диапазоне от 1 до p-1.
5. Выбирается случайное число k от 0 до q.
6. Вычисляется r = (gk mod p) mod q.
7. Затем s = k-1(H(m) + xr)) mod q.
8. Если r=0 или s=0, выбирается другое число k.

Схема Эль-Гамаля

Шифрование по схеме Эль-Гамаля используется для цифровых подписей. Является продолжением алгоритма Диффи-Хеллмана.

При работе по этой схеме важно учитывать следующую особенность. Шифрование Эль-Гамаля не является алгоритмом цифровой подписи по схеме с одноименным названием. При шифровке текст преобразовывается в шифр, который длиннее исходного сообщения в 2 раза.

Генерация ключей происходит следующим образом.

1. Выбирается случайное простое число p.
2. Число g должно быть первообразным корнем p.
3. Число x должно быть больше 1 и меньше p-1. Это будет закрытый ключ.
4. Затем вычисляется открытый ключ y по формуле g^x mod p.

При шифровании текста M выбирается системный ключ K. Он больше единицы и меньше p-1. Затем вычисляются числа a и b, которые являются шифротекстом, a = g^k mod p и b = y^k M mod p.

fb.ru

1.2 Симметричная криптография (одноключевая, с секретным ключом)

Термин	Значение	Замечания
Симметричная методология	Используется один ключ, с помощью которого производится как шифрование, так и расшифровка с использованием одного и того же алгоритма симметричного шифрования. Этот ключ передается двум участникам взаимодействия безопасным образом до передачи зашифрованных данных.	Часто называется методологией с секретным ключом.
Асимметричная методология	Использует алгоритмы симметричного шифрования и симметричные ключи для шифрования данных Использует алгоритмы асимметричного шифрования и асимметричные ключи для шифрования симметричного ключа. Создаются два взаимосвязанных асимметричных ключа. Симметричный ключ, зашифрованный с использованием одного асимметричного ключа и алгоритма асимметричного шифрования, должен расшифровываться с использованием другого ключа и того же алгоритма шифрования. Создаются два взаимосвязанных асимметричных ключа. Один должен быть безопасно передан его владельцу, а другой — тому лицу, которое отвечает за хранение этих ключей (CA — сертификационному центру ключей), до начала их использования.	Часто называется методологией с открытым ключом
Секретный ключ(1)	Симметричная методология	Используется один ключ, с помощью которого производится как шифрование, так и расшифровка. См. выше
Секретный ключ(2)	Секретный ключ симметричного шифрования	Симметричный секретный ключ
Секретный ключ(3)	Секретный ключ асимметричного шифрования	Асимметричный секретный ключ Асимметричные ключи создаются парами, так как связаны друг с другом. Выражение «секретный ключ» часто используют для одного из пары асимметричных ключей, который должен держаться в секрете. Асимметричный секретный ключ не имеет ничего общего с симметричным секретным ключом.
Открытый ключ (1)	Асимметричная методология	Использует пару ключей, которые совместно создаются и связаны друг с другом. Все, что зашифровано одним ключом, может быть расшифровано только другим ключом этой пары.
Открытый ключ (2)	Открытый ключ асимметричного шифрования	Асимметричные ключи создаются парами, каждый из двух ключей связан с другим. Выражение «открытый ключ» часто используют для одного из пары асимметричных ключей, который должен быть всем известен.
Сеансовый ключ	Симметричный (секретный) ключ шифрования	Используется в асимметричной методологии для шифрования самих данных с помощью симметричных методологий. Это просто симметричный секретный ключ (см. выше)
Алгоритм шифрования	Математическая формула	Для симметричных алгоритмов требуются симметричные ключи. Для асимметричных алгоритмов требуются асимметричные ключи. Вы не можете использовать симметричные ключи для асимметричных алгоритмов и наоборот.
Секретные криптосистемы	Используют симметричные алгоритмы и симметричные (секретные) ключи для шифрования данных.
Открытые криптосистемы	Использует асимметричные алгоритмы и асимметричные ключи для шифрования сеансовых ключей. Используют симметричные алгоритмы и симметричные (секретные) ключи для шифрования данных.

studfiles.net

1.2 Симметричная и асимметричная криптография.

Говоря о симметричном и ассиметричном шифровании мы сразу подразумеваем понятия «шифра» и «шифрование сообщений», поэтому постараемся дать основные концепции данных терминов.

Рассмотрим основные концепции шифрования на примере схемы (схема является примером симметричного шифрования):

В процессе шифрования используется определенный алгоритм шифрования, на вход которому подается исходное незашифрованное сообщение и ключ. Выходом алгоритма является сообщение исходное сообщение, которое было зашифровано. Ключ является значением, не зависящим от шифруемого сообщения. Изменение ключа должно приводить и к изменению зашифрованного сообщения.

Зашифрованное сообщение передается получателю. Получатель преобразует зашифрованное сообщение в исходное до зашифровки сообщение с помощью алгоритма дешифрования и того же самого ключа, который используется при шифровании, или ключа, легко получаемого из ключа шифрования.

Безопасность, обеспечиваемая традиционной криптографией при симметричном шифровании, зависит от нескольких факторов.

Во-первых, криптографический алгоритм должен быть достаточно сильным, чтобы передаваемое зашифрованное сообщение невозможно было расшифровать без ключа, используя только различные статистические закономерности зашифрованного сообщения или какие-либо другие способы его анализа.

Во-вторых, безопасность передаваемого сообщения должна зависеть от секретности ключа, но не от секретности алгоритма. Алгоритм должен быть проанализирован специалистами, чтобы исключить наличие слабых мест, при которых плохо скрыта взаимосвязь между незашифрованным и зашифрованным сообщением. К тому же при выполнении этого условия производители могут создавать дешевые аппаратные чипы и свободно распространяемые программы, реализующие данный алгоритм шифрования.

В-третьих, алгоритм должен быть таким, чтобы нельзя было узнать ключ, даже зная достаточно много пар (зашифрованное сообщение, незашифрованное сообщение), полученных при шифровании с использованием данного ключа.

Клод Шеннон¹ ввел понятия диффузии и конфузии для описания стойкости алгоритма шифрования.

Диффузия – это рассеяние статистических особенностей и закономерностей незашифрованного текста в широком диапазоне статистических особенностей и закономерностей зашифрованного текста. Это достигается тем, что значение каждого элемента незашифрованного текста влияет на значения многих элементов зашифрованного текста или, что то же самое, любой элемент зашифрованного текста зависит от многих элементов незашифрованного текста.

Конфузия – это уничтожение статистической взаимосвязи между зашифрованным текстом и ключом.

Если X – это исходное сообщение и K – криптографический ключ, то зашифрованный передаваемый текст можно записать в виде , где Y – это полученное зашифрованное сообщение.

Получатель, используя тот же ключ, расшифровывает сообщение .

Противник, не имея доступа к K и X, должен попытаться узнать X, K или и то, и другое.

Алгоритмы симметричного шифрования различаются способом, которым обрабатывается исходный текст. Возможно шифрование блоками или шифрование потоком.

Блок текста рассматривается как неотрицательное целое число, либо как несколько независимых неотрицательных целых чисел. Длина блока всегда выбирается равной степени двойки.

Операции симметричного шифрования циклически повторяются в алгоритме, образуя так называемые раунды или шаги (не путайте с криптографическим протоколом!). Входом каждого раунда является выход предыдущего раунда и ключ, который получен по определенному алгоритму из ключа шифрования K. Ключ раунда называется подключом. Каждый алгоритм шифрования может быть представлен в виде следующей схемы:

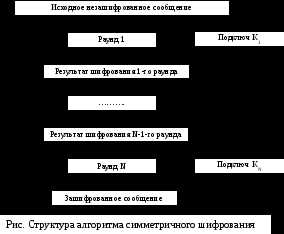
Рис.1.2. Упрощённая схема алгоритма шифрования.

Стандартный алгоритм шифрования (не только симметричного) должен быть применим во многих приложениях:

• шифрование данных. Алгоритм должен быть эффективен при шифровании файлов данных или большого потока данных.

• создание случайных чисел. Алгоритм должен быть эффективен при создании определенного количества случайных битов.

• хэширование. Алгоритм должен эффективно преобразовываться в одностороннюю хэш-функцию.

Эти требования являются основой для создания алгоритма шифрования. Теперь выделим ряд дополнительных требований, которые желательно соблюдать для упрощения создания алгоритма и его последующего функционирования:

• алгоритм должен быть простым для написания кода, чтобы минимизировать вероятность программных ошибок.

• алгоритм должен иметь плоское пространство ключей, т.е. допускать любую случайную строку битов нужной длины в качестве возможного ключа. Наличие слабых ключей нежелательно.

• алгоритм должен легко модифицироваться для различных уровней безопасности и удовлетворять как минимальным, так и максимальным требованиям.

• все операции с данными должны осуществляться над блоками, кратными байту или 32-битному слову.

Несмотря на эффективность симметричных систем шифрования, они не могут обеспечить комплексной информации безопасности. Для этого были разработаны системы ассиметричного шифрования или системы с открытым ключом.

Алгоритм шифрования с открытым ключом разрабатывались для того, чтобы решить две наиболее трудные задачи, возникшие при использовании симметричного шифрования.

Первой задачей является распределение ключа. При симметричном шифровании требуется, чтобы обе стороны уже имели общий ключ, который каким-то образом должен быть им заранее передан, что отрицает всю суть криптографии, по мнению Уитфилда Диффи, а именно возможность поддерживать всеобщую секретность при коммуникациях.

Второй задачей является необходимость создания таких механизмов, при использовании которых невозможно было бы подменить кого-либо из участников, т.е. нужна цифровая подпись. При использовании коммуникаций для решения широкого круга задач, например в коммерческих и частных целях, электронные сообщения и документы должны иметь эквивалент подписи, содержащейся в бумажных документах. Для этого необходимо создать метод, при использовании которого все участники будут убеждены, что электронное сообщение было послано конкретным участником. Это более сильное требование, чем аутентификация. Под аутентификацией понимают установление подлинности конкретного участника, например, путем сравнения вводимого пароля и пароля из базы данных.

Преимущество систем с открытыми ключами состоит в том, что каждому пользователю нужен только один секрет, который он ни с кем не разделяет. При этом громоздкая и трудоемкая в создании и поддержании матрица симметричных ключей вырождается в один столбец, который владеет (управляет) только своим секретом, что существенно расширяет масштабы применения криптосистем.

Обозначим основные понятия, которые нам необходимы.

Шифрование с открытым ключом является асимметричным, поскольку использует два различных ключа для шифрования и дешифрования (см. Рис. Алгоритм асимметричного шифрования).

Пара ключей, используемых при ассиметричном шифровании, называются открытым ключом (public key), который доступен всем пользователям, и закрытым ключом (private key), который держится в тайне, соответственно. В любое время участник может изменить свой закрытый ключ и опубликовать из новой составленной пары открытый ключ, заменив им старый опубликованный.

Главное достижение асимметричного шифрования в том, что оно позволяет людям, не имеющим существующей договорённости о безопасности, обмениваться секретными сообщениями. Необходимость отправителю и получателю согласовывать тайный ключ по специальному защищённому каналу полностью отпадает. Все коммуникации затрагивают только открытые ключи, тогда как закрытые хранятся в безопасности.

studfiles.net

📌 Симметричные криптосистемы — это… 🎓 Что такое Симметричные криптосистемы?

Симметри́чные криптосисте́мы (также симметричное шифрование, симметричные шифры) — способ шифрования, в котором для шифрования и расшифровывания применяется один и тот же криптографический ключ. До изобретения схемы асимметричного шифрования единственным существовавшим способом являлось симметричное шифрование. Ключ алгоритма должен сохраняться в секрете обеими сторонами. Алгоритм шифрования выбирается сторонами до начала обмена сообщениями.

Основные сведения

Алгоритмы шифрования и дешифрования данных широко применяются в компьютерной технике в системах сокрытия конфиденциальной и коммерческой информации от злонамеренного использования сторонними лицами. Главным принципом в них является условие, что передатчик и приемник заранее знают алгоритм шифрования, а также ключ к сообщению, без которых информация представляет собой всего лишь набор символов, не имеющих смысла.

Классическим примером таких алгоритмов являются симметричные криптографические алгоритмы, перечисленные ниже:

• Простая перестановка
• Одиночная перестановка по ключу
• Двойная перестановка
• Перестановка «Магический квадрат»

Простая перестановка

Простая перестановка без ключа — один из самых простых методов шифрования. Сообщение записывается в таблицу по столбцам. После того, как открытый текст записан колонками, для образования шифровки он считывается по строкам. Для использования этого шифра отправителю и получателю нужно договориться об общем ключе в виде размера таблицы. Объединение букв в группы не входит в ключ шифра и используется лишь для удобства записи несмыслового текста.

Одиночная перестановка по ключу

Более практический метод шифрования, называемый одиночной перестановкой по ключу очень похож на предыдущий. Он отличается лишь тем, что колонки таблицы переставляются по ключевому слову, фразе или набору чисел длиной в строку таблицы.

Двойная перестановка

Для дополнительной скрытности можно повторно шифровать сообщение, которое уже было зашифровано. Этот способ известен под названием двойная перестановка. Для этого размер второй таблицы подбирают так, чтобы длины ее строк и столбцов были другие, чем в первой таблице. Лучше всего, если они будут взаимно простыми. Кроме того, в первой таблице можно переставлять столбцы, а во второй строки. Наконец, можно заполнять таблицу зигзагом, змейкой, по спирали или каким-то другим способом. Такие способы заполнения таблицы если и не усиливают стойкость шифра, то делают процесс шифрования гораздо более занимательным.

Перестановка «Магический квадрат»

Магическими квадратами называются квадратные таблицы со вписанными в их клетки последовательными натуральными числами от 1, которые дают в сумме по каждому столбцу, каждой строке и каждой диагонали одно и то же число. Подобные квадраты широко применялись для вписывания шифруемого текста по приведенной в них нумерации. Если потом выписать содержимое таблицы по строкам, то получалась шифровка перестановкой букв. На первый взгляд кажется, будто магических квадратов очень мало. Тем не менее, их число очень быстро возрастает с увеличением размера квадрата. Так, существует лишь один магический квадрат размером 3 х 3, если не принимать во внимание его повороты. Магических квадратов 4 х 4 насчитывается уже 880, а число магических квадратов размером 5 х 5 около 250000. Поэтому магические квадраты больших размеров могли быть хорошей основой для надежной системы шифрования того времени, потому что ручной перебор всех вариантов ключа для этого шифра был немыслим.

В квадрат размером 4 на 4 вписывались числа от 1 до 16. Его магия состояла в том, что сумма чисел по строкам, столбцам и полным диагоналям равнялась одному и тому же числу — 34. Впервые эти квадраты появились в Китае, где им и была приписана некоторая «магическая сила».

16	3	2	13
5	10	11	8
9	6	7	12
4	15	14	1

Шифрование по магическому квадрату производилось следующим образом. Например, требуется зашифровать фразу: «ПриезжаюCегодня.». Буквы этой фразы вписываются последовательно в квадрат согласно записанным в них числам: позиция буквы в предложении соответствует порядковому числу. В пустые клетки ставится точка.

16.	3 и	2 р	13 д
5 з	10 е	11 г	8 ю
9 С	6 ж	7 а	12 о
4 е	15 я	14 н	1 П

После этого шифрованный текст записывается в строку (считывание производится слева направо, построчно):
.ирдзегюСжаоеянП

При расшифровывании текст вписывается в квадрат, и открытый текст читается в последовательности чисел «магического квадрата» Программа должна генерировать «магические квадраты» и по ключу выбирать необходимый. Размер квадрата больше чем 3х3.

История

Требования

Полная утрата всех статистических закономерностей исходного сообщения является важным требованием к симметричному шифру. Для этого шифр должен иметь «эффект лавины» — должно происходить сильное изменение шифроблока при 1битном изменении входных данных (в идеале должны меняться значения 1/2 бит шифроблока).

Также важным требованием является отсутствие линейности (то есть условия f(a) xor f(b) == f(a xor b)), в противном случае облегчается применение дифференциального криптоанализа к шифру.

Общая схема

В настоящее время симметричные шифры — это:

• блочные шифры. Обрабатывают информацию блоками определённой длины (обычно 64, 128 бит), применяя к блоку ключ в установленном порядке, как правило, несколькими циклами перемешивания и подстановки, называемыми раундами. Результатом повторения раундов является лавинный эффект — нарастающая потеря соответствия битов между блоками открытых и зашифрованных данных.

• поточные шифры, в которых шифрование проводится над каждым битом либо байтом исходного (открытого) текста с использованием гаммирования. Поточный шифр может быть легко создан на основе блочного (например, ГОСТ 28147-89 в режиме гаммирования), запущенного в специальном режиме.

Большинство симметричных шифров используют сложную комбинацию большого количества подстановок и перестановок. Многие такие шифры исполняются в несколько (иногда до 80) проходов, используя на каждом проходе «ключ прохода». Множество «ключей прохода» для всех проходов называется «расписанием ключей» (key schedule). Как правило, оно создается из ключа выполнением над ним неких операций, в том числе перестановок и подстановок.

Типичным способом построения алгоритмов симметричного шифрования является сеть Фейстеля. Алгоритм строит схему шифрования на основе функции F(D, K), где D — порция данных, размером вдвое меньше блока шифрования, а K — «ключ прохода» для данного прохода. От функции не требуется обратимость — обратная ей функция может быть неизвестна. Достоинства сети Фейстеля — почти полное совпадение дешифровки с шифрованием (единственное отличие — обратный порядок «ключей прохода» в расписании), что сильно облегчает аппаратную реализацию.

Операция перестановки перемешивает биты сообщения по некоему закону. В аппаратных реализациях она тривиально реализуется как перепутывание проводников. Именно операции перестановки дают возможность достижения «эффекта лавины». Операция перестановки линейна — f(a) xor f(b) == f(a xor b)

Операции подстановки выполняются как замена значения некоей части сообщения (часто в 4, 6 или 8 бит) на стандартное, жестко встроенное в алгоритм иное число путем обращения к константному массиву. Операция подстановки привносит в алгоритм нелинейность.

Зачастую стойкость алгоритма, особенно к дифференциальному криптоанализу, зависит от выбора значений в таблицах подстановки (S-блоках). Как минимум считается нежелательным наличие неподвижных элементов S(x) = x, а также отсутствие влияния какого-то бита входного байта на какой-то бит результата — то есть случаи, когда бит результата одинаков для всех пар входных слов, отличающихся только в данном бите.

Параметры алгоритмов

Существует множество (не менее двух десятков) алгоритмов симметричных шифров, существенными параметрами которых являются:

• стойкость
• длина ключа
• число раундов
• длина обрабатываемого блока
• сложность аппаратной/программной реализации
• сложность преобразования

Распространенные алгоритмы

• AES (англ. Advanced Encryption Standard) — американский стандарт шифрования
• ГОСТ 28147-89 — отечественный стандарт шифрования данных
• DES (англ. Data Encryption Standard) — стандарт шифрования данных в США

Сравнение с асимметричными криптосистемами

Достоинства

• скорость (по данным Applied Cryptography — на 3 порядка выше)
• простота реализации (за счёт более простых операций)
• меньшая требуемая длина ключа для сопоставимой стойкости
• изученность (за счёт большего возраста)

Недостатки

• сложность управления ключами в большой сети. Означает квадратичное возрастание числа пар ключей, которые надо генерировать, передавать, хранить и уничтожать в сети. Для сети в 10 абонентов требуется 45 ключей, для 100 уже 4950, для 1000 — 499500 и т. д.
• сложность обмена ключами. Для применения необходимо решить проблему надёжной передачи ключей каждому абоненту, так как нужен секретный канал для передачи каждого ключа обеим сторонам.

Для компенсации недостатков симметричного шифрования в настоящее время широко применяется комбинированная (гибридная) криптографическая схема, где с помощью асимметричного шифрования передаётся сеансовый ключ, используемый сторонами для обмена данными с помощью симметричного шифрования.

Важным свойством симметричных шифров является невозможность их использования для подтверждения авторства, так как ключ известен каждой стороне.

Литература

• Гатчин Ю.А., Коробейников А.Г. Основы криптографических алгоритмов. Учебное пособие. — СПб.: СПбГИТМО(ТУ), 2002.
• Кон П. Универсальная алгебра. — М.: Мир. — 1968.
• Коробейников А. Г. Математические основы криптографии. Учебное пособие. СПб: СПб ГИТМО (ТУ), 2002.

Ссылки

dic.academic.ru

Симметричное шифрование Википедия

Симметри́чные криптосисте́мы (также симметричное шифрование, симметричные шифры) (англ. symmetric-key algorithm) — способ шифрования, в котором для шифрования и расшифровывания применяется один и тот же криптографический ключ. До изобретения схемы асимметричного шифрования единственным существовавшим способом являлось симметричное шифрование. Ключ алгоритма должен сохраняться в тайне обеими сторонами, осуществляться меры по защите доступа к каналу, на всем пути следования криптограммы, или сторонами взаимодействия посредством криптообьектов, сообщений, если данный канал взаимодействия под грифом «Не для использования третьими лицами». Алгоритм шифрования выбирается сторонами до начала обмена сообщениями.

Основные сведения[ | ]

Алгоритмы шифрования данных широко применяются в компьютерной технике в системах сокрытия конфиденциальной и коммерческой информации от злонамеренного использования сторонними лицами. Главным принципом в них является условие, что передатчик и приемник заранее знают алгоритм шифрования, а также ключ к сообщению, без которых информация представляет собой всего лишь набор символов, не имеющих смысла.

Классическими примерами таких алгоритмов являются симметричные криптографические алгоритмы, перечисленные ниже:

• Простая перестановка
• Одиночная перестановка по ключу
• Двойная перестановка
• Перестановка «Магический квадрат»

Простая перестановка[ | ]

Простая перестановка без ключа — один из самых простых методов шифрования. Сообщение записывается в таблицу по столбцам. После того, как открытый текст записан колонками, для образования шифртекста он считывается по строкам. Для использования этого шифра отправителю и получателю нужно договориться об общем ключе в виде размера таблицы. Объединение букв в группы не входит в ключ шифра и используется лишь для удобства записи несмыслового текста.

Одиночная перестановка по ключу[ | ]

Более практический метод шифрования, называемый одиночной перестановкой по ключу, очень похож на предыдущий. Он отличается лишь тем, что колонки таблицы переставляются по ключевому слову, фразе или набору чисел длиной в строку таблицы.

Двойная перестановка[ | ]

Для дополнительной скрытности можно повторно шифровать сообщение, которое уже было зашифровано. Этот способ известен под названием двойная перестановка. Для этого размер второй таблицы подбирают так, чтобы длины её строк и столбцов отличались от длин в первой таблице. Лучше всего, если они будут взаимно простыми. Кроме того, в первой таблице можно переставлять столбцы, а во второй строки. Наконец, можно заполнять таблицу зигзагом, змейкой, по спирали или каким-то другим способом. Такие способы заполнения таблицы если и не усиливают стойкость шифра, то делают процесс шифрования гораздо более занимательным.

ru-wiki.ru